
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Нормальное преобразование и его свойства
|
|
Преобразование называется нормальным, если оно перестановочно с сопряженным преобразованием, то есть  .
.
Свойство 8.4. Если x собственный вектор нормального преобразования  с собственным значением
с собственным значением  , то x собственный вектор
, то x собственный вектор  с собственным значением
с собственным значением  .
.
Доказательство. Пусть 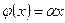 . Поскольку
. Поскольку  и
и  , то
, то 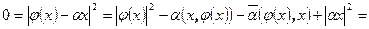
 .
.
Свойство 8.5. Собственные векторы нормального преобразования, соответствующие разным собственным значениям ортогональны.
Доказательство. Пусть x и y – собственные векторы нормального преобразования  , соответствующие разным собственным значениям
, соответствующие разным собственным значениям  и
и  (
(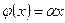 ,
,  ). Из равенств
). Из равенств  и
и  (Свойство 8.4) выводим
(Свойство 8.4) выводим  ,
,  ,
,  ,
,  . Далее,
. Далее,  , откуда
, откуда  .
.
Теорема 8.1. Для нормального преобразования конечномерного унитарного пространства существует ортонормированный базис из собственных векторов.
Доказательство. Путь  - ортонормированный базис унитарного пространства V, в котором матрица нормального преобразования
- ортонормированный базис унитарного пространства V, в котором матрица нормального преобразования  является верхней треугольной. Пусть
является верхней треугольной. Пусть  , тогда
, тогда  . Из равенства
. Из равенства 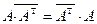 вытекает, что матрица A – диагональная, и, значит, базис
вытекает, что матрица A – диагональная, и, значит, базис  составлен из собственных векторов.
составлен из собственных векторов.
Построение ортонормированного базиса из собственных векторов, в котором матрица нормального преобразования диагонализируема, можно осуществлять следующим образом. Найти какой ни будь базис из собственных векторов. При этом, собственные векторы, соответствующие разным собственным числам заведомо ортогональны (Свойство 8.5). Условие ортогональности может нарушаться только на собственных векторах, соответствующих одному и тому же собственному значению.
Если матрица линейного преобразования диагонализируема, то всегда можно ввести скалярное произведение таким образом, чтобы линейное преобразование стало нормальным.
Теорема 8.2. Для нормального преобразования конечномерного евклидова пространства существует ортонормированный базис, в котором матрица линейного преобразования имеет блочно-диагональный вид. По главной диагонали расположены блоки первого и второго порядка.
Доказательство. Путь  - ортонормированный базис евклидова пространства V, в котором матрица нормального преобразования
- ортонормированный базис евклидова пространства V, в котором матрица нормального преобразования  является блочной верхней треугольной. Пусть
является блочной верхней треугольной. Пусть  , тогда
, тогда  . Из равенства
. Из равенства  вытекает, что матрица A – блочно диагональная, что и требовалось доказать.
вытекает, что матрица A – блочно диагональная, что и требовалось доказать.
К сожалению, приведенное доказательство не раскрывает структуру блоков второго порядка, расположенных на главной диагонали. Поэтому дадим другое доказательство этой теоремы.
Доказательство 2. Множество  является линейным пространством над полем комплексных чисел C. В этом линейном пространстве введем скалярное произведение
является линейным пространством над полем комплексных чисел C. В этом линейном пространстве введем скалярное произведение  . Определим линейное преобразование пространства
. Определим линейное преобразование пространства  как
как  . Пусть
. Пусть  - ортонормированный базис
- ортонормированный базис  , тогда
, тогда  - ортонормированный базис унитарного пространства
- ортонормированный базис унитарного пространства  и
и  - матрица с вещественными элементами. Далее,
- матрица с вещественными элементами. Далее,  ,
,  и из равенства матриц
и из равенства матриц  выводим равенство
выводим равенство  , то есть преобразование
, то есть преобразование  - нормальное. Следовательно, существует ортонормированный базис
- нормальное. Следовательно, существует ортонормированный базис  унитарного пространства
унитарного пространства  из собственных векторов нормального преобразования
из собственных векторов нормального преобразования  . Пусть
. Пусть  - собственные числа этих векторов. Заметим, что ортонормированный базис
- собственные числа этих векторов. Заметим, что ортонормированный базис  получается объединением ортонормированных базисов подпространств
получается объединением ортонормированных базисов подпространств 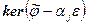 . Если собственное число
. Если собственное число  вещественное, то ортонормированный базис подпространства
вещественное, то ортонормированный базис подпространства  является также ортонормированным базисом подпространства
является также ортонормированным базисом подпространства  . Поэтому, не нарушая общности можно считать, что вещественным собственным числам в базисе
. Поэтому, не нарушая общности можно считать, что вещественным собственным числам в базисе  соответствуют векторы из V. Пусть f = x + iy – собственный вектор
соответствуют векторы из V. Пусть f = x + iy – собственный вектор  с комплексным собственным числом
с комплексным собственным числом  , тогда из равенств
, тогда из равенств  и
и  выводим
выводим  ,
,  , то есть линейное подпространство, натянутое на векторы x, y – инвариантно. Из полученных равенств вытекает
, то есть линейное подпространство, натянутое на векторы x, y – инвариантно. Из полученных равенств вытекает  , то есть вектор x - iy – собственный с собственным числом
, то есть вектор x - iy – собственный с собственным числом  . Если
. Если  ортонормированный базис
ортонормированный базис  , то
, то  - ортонормированный базис
- ортонормированный базис  , поэтому, можно считать, что в базисе
, поэтому, можно считать, что в базисе  собственные векторы с комплексными собственными числами разбиты на пары. Рассмотрим пару
собственные векторы с комплексными собственными числами разбиты на пары. Рассмотрим пару  ,
,  собственных векторов с собственными числами
собственных векторов с собственными числами  и
и  . Эти векторы ортогональны всем остальным векторам из базиса, следовательно, векторы
. Эти векторы ортогональны всем остальным векторам из базиса, следовательно, векторы  ортогональны всем остальным векторам. Далее,
ортогональны всем остальным векторам. Далее,  , откуда выводим
, откуда выводим  и
и  . Заменим векторы
. Заменим векторы  и
и 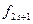 на
на  получим ортонормированный базис пространства V, в котором матрица линейного преобразования имеет блочно диагональный вид. По главной диагонали расположены блоки первого порядка, отвечающие вещественным собственным значениям, и блоки второго порядка
получим ортонормированный базис пространства V, в котором матрица линейного преобразования имеет блочно диагональный вид. По главной диагонали расположены блоки первого порядка, отвечающие вещественным собственным значениям, и блоки второго порядка  , отвечающие
, отвечающие  комплексным собственным значениям.
комплексным собственным значениям.
Если матрица линейного преобразования диагонализируема, то всегда можно ввести скалярное произведение таким образом, чтобы линейное преобразование стало нормальным.
Date: 2016-06-08; view: 462; Нарушение авторских прав