Средние величины, методика их вычисления и оценка достоверности

В медико-социальных исследованиях наряду с абсолютными и относительными широко используются средние величины. Средняя величина – это совокупная обобщающая характеристика количественных признаков, она обычно обозначается буквой М или Х. Средние величины существенно отличаются от статистических коэффициентов:

1. Коэффициенты характеризуют признак, встречающийся только у некоторой части статистического коллектива, так называемый альтернативный признак, который может иметь место или не иметь место (рождение, смерть, заболевание, инвалидность).

Средние величины охватывают признаки, присущие всем членам коллектива, но в разной степени (вес, рост, дни лечения в больнице).

2. Коэффициенты применяются для измерения качественных признаков. Средние величины — для варьирующих количественных признаков.

Применение средних величин в медико-социальных исследо­ваниях широко используется при изучении физического раз­вития. Кроме того, средние величины применяются:

1. Для характеристики организации работы лечебно-профи­лактических учреждений и оценки их деятельности:

а) в поликлинике: показатели нагрузки врачей, посещаемость поликлиники, среднее число посещений на 1-м году жизни, среднее число детей на участке, среднее число посещений при определенном заболевании и т. д.;

б) в стационаре: среднее число дней работы койки в году; средняя длительность лечения при определенных заболеваниях и т. д.;

в) в органах санэпиднадзора: средняя площадь (или кубатура) на 1 человека, средние нормы питания (белки, жиры, углеводы, витамины, минеральные соли, калории) в дневном рационе возрастных групп у детей и взрослых и т. д.

2. Для определения медико-физиологических показателей орга­низма в норме и патологии в клинических и эксперименталь­ных исследованиях.

3. В специальных демографических и медико-социальных исследованиях.

Для расчета средней величины необходимо построить вариационный ряд — т. е. ряд числовых измерений определенного признака, отличающихся по своей величине.

Вариационные ряды бывают следующих видов:

а) ранжированный, неранжированный;

б) сгруппированный, несгруппированный;

в) прерывный, непрерывный.

Ранжированный ряд — упорядоченный ряд; варианты располагаются последовательно по нарастанию или убыванию числовых значений.

Неранжированный ряд — варианты располагаются бессистемно.

Прерывный (дискретный) ряд — варианты выражены в виде целых (дискретных) чисел (окна в избе).

Непрерывный ряд – варианты могут быть выражены дробными числами.

Несгруппированный ряд – каждому значению варианты соответствует определенное число частот.

Сгруппированный ряд (интервальный) – варианты соединены в группы, объединяющие их по величине в пределах определенного интервала.

В статистике принято выделять следующие виды средних величин: мода (Мо), медиана (Ме) и средняя арифметическая (М). Мода – величина варьирующего признака, наиболее часто встречающаяся в совокупности. В вариационном ряду это варианта, имеющая наибольшую частоту встречаемости. Обычно мода является величиной довольно близкой к средней арифметической, совпадает с ней при полной симметрии распределения. Медиана – варианта, делящая вариационный ряд на две равные половины. При нечетном числе наблюдений медианой является варианта, имеющая в вариационном ряду порядковый номер (n + 1): 2. Средняя арифметическая величина (М) – в отличие от моды и медианы опирается на все произведенные наблюдения, поэтому является важной характеристикой для всего распределения.

В зависимости от вида вариационного ряда используется тот или иной способ расчета средней. Средняя арифметическая для простого ряда, где каждая варианта встречается один раз, вычисляется по формуле: М = , где 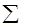- знак суммы, V –отдельные значения вариант, n –число наблюдений. Средняя арифметическая взвешенная определяется по формуле: М= , где 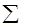- знак суммы, V –отдельные значения вариант, n –число наблюдений, р – частота встречаемости вариант. Одним из наиболее простых и достаточно точных способов расчета средней арифметической является способ моментов, основанный на том, что алгебраическая сумма отклонений каждой варианты вариационного ряда от средней арифметической равна нулю. М= А + i , где А – условно принятая средняя или мода, а - отклонение каждой варианты от условно принятой средней, р –частота встречаемости вариант, n –число наблюдений, i – интервал или расстояние между соседними вариантами. Основные свойства средней величины: 1) имеет абстрактный характер, так как является обобщающей величиной: в ней стираются случайные колебания; 2) занимает срединное положение в ряду (в строго симметричном ряду); 3) сумма отклонений всех вариант от средней величины равна нулю. Данное свойство средней величины используется для проверки правильности расчета средней. Она оценивается по уровню колеблемости вариационного ряда. Критериями такой оценки могут служить: амплитуда (разница между крайними вариантами); среднее квадратическое отклонение, показывающее, как отличаются варианты от рассчитанной средней величины; коэффициент вариации.

Среднеквадратическое отклонение () наиболее точно характеризует степень разнообразия варьирующего признака, без чего нельзя достаточно полно охарактеризовать явление. Для простого вариационного ряда (р =1) среднеквадратическое отклонение расчитывается по формуле . Для взвешенного вариационного ряда по формуле:

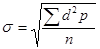, где d = V – M - отклонение каждой варианты от средней арифметической. При числе наблюдений меньше 30 в знаменателе этих формул берется не n, а n – 1 (так называемое в статистике число степеней свободы). При числе наблюдений более 30 уменьшение знаменателя на единицу не имеет практического значения, т.к. существенно не сказывается на конечном результате. Значительно упрощает вычисления расчет среднего квадратического отклонения по способу моментов.

где, величина называется моментом первой степени, а - моментом второй степени.

Степень разнообразия (колеблемости) признака в вариационном ряду можно оценить по коэффициенту вариации (отношение среднего квадратического отклонения к средней величине, умноженное на 100%); при вариации менее 10% отмечается слабое разнообразие, при вариации 10—20% — среднее, а при вариации более 20% — сильное разнообразие признака. Если нет возможности сравнить вариационный ряд с другими, то используют правило трех сигм. Если к средней прибавить одну сигму, то этой вычисленной средней соответствует 68,3%, при двух сигмах — 95,4%, при трех сигмах — 99,7% от всех признаков. В медицине с величиной М ± 1σ связано понятие нормы; отклонения от средней (в любую сторону) больше, чем на 1σ, но меньше чем на 2σ, считаются субнормальными (выше или ниже нормы), а при отклонении от средней больше чем на 2σ, варианты считаются значительно отличающимися от нормы (патология).

Мерой точности и достоверности результатов выборочных статистических величин являются средние ошибки представительности (репрезентативности). Средняя ошибка средней арифметической – m (отношение среднего квадратического отклонения к квадратному корню из общего числа наблюдений — объектов). m =

Мерой достоверности среднего показателя наряду с его ошибкой являются, доверительные границы и достоверность разности между двумя средними величинами.

Date: 2016-02-19; view: 776; Нарушение авторских прав