Оценивание состояния линеаризованной системы с модальным регулятором при внешних неопределенных ограниченных возмущениях

Пусть в начальный момент времени t₀ состояние системы является неопределенным, известно, что оно принадлежит эллипсоиду, где Q₀∈ G⁺ – заданная положительно определенная симметрическая матрица. Предполагается, что пара (A,D) –управляема, а матрица C является матрицей полного ранга строк.

Требуется на заданном интервале времени получить эллипсоидальную оценку множества состояний для процессов системы, начинающихся из заданного эллипсоида при E (Q₀) и неопределенных возмущениях, а также установить ограниченность решений исходной системы на конечном интервале относительно заданных множеств.

Инвариантные эллипсоиды характеризуют внешнюю оценку области достижимости в текущий момент времени t при влиянии неопределенных внешних возмущений w(t) на траектории системы. В этой связи нас будет интересовать минимальные (в некотором смысле) инвариантные эллипсоиды, содержащие траектории или выход z(t) рассматриваемой системы.

%-----модель математического маятника -------

% Примеры синтеза оценивания состояния и моделирования

%--Исходные данные --Линеаризованная модель с неопределенными возмущениями

% вектор состояния x=(x1,x2)T

clc;

n=2;

m=1;

l=0.5;

Ip=0.05;

g=9.8;

mlp=m*l*l+Ip;

mgl=m*l*g;

Ri = 2.6;

kg =3.7;

KM=0.00767*100;

bet=kg*KM;

btet=0.025;

tet0=5*pi/9;

cs0=cos(tet0);

V0=mgl*sin(tet0)*Ri/bet;

n1=n;

betR=bet/Ri;

btetbR=btet+bet*betR;

A = [0 1; -mgl*cs0/mlp -btetbR/mlp];

B1 = [0; bet/Ri/mlp];

D=[0; -1/mlp]/20;

C=[1 0;0 1;0 0];

Cy=[1 0];

B2=[0; 0;1];

n1=n;

mu1=1;

eig(A)

p=[0. -11];

K0=-place(A,B1,p);

ABK0=A+B1*K0;

% Нахождение предельного инвариантного эллипсоида замкнутой системы с

% матрицей A+B*K0 и оптимизацией по параметру q;

A0=ABK0;

min_tr_Q=1e+4;

for q = 0.1:0.002:1;% 0.944:0.002:0.944

cvx_begin sdp

variable Qs(n, n) symmetric;

minimize(trace(Qs))

subject to

Qs >= eye(2)*10e-5;

[A0*Qs + Qs*A0'+q*Qs D;

D' -q*eye(1)]< 0; %условие асимптотич устойчивости

cvx_end

Qsf = double(Qs)

trQ=trace(Qsf);

if min_tr_Q > trQ

min_tr_Q = trQ;

Q_min = Qsf;

q_min = q

end;

end;

Q0 = Q_min;

q0=q_min;

С помощью данной программы в пакете Matlab матрица минимального инвариантного эллипсоида

При q0=q_min=1.

Построим оценку состояния линеаризованной системы с неопределенными ограниченными возмущениями. Для численного интегрирования МСС на заданном интервале [t0,tk] использовалась стандартная функция пакета Matlab ode15s, вызов которой показан в следующем фрагменте программы.

%Эллипсоид

% Оценивание состояния маятника с неопределенными возмущениями с помощью

% матричной системы сравнения

t0=0; tk=10;

Q=[1 0; 0 1];

vec_Q = [Q(:,1); Q(:,2)];

[t,H] =ode15s(@(t,vec_Q) Prav_Lin_Mayat_1(t,vec_Q,A0,D,q0),[t0 tk],vec_Q);

MQ = [];

nh=length(H(:,1));

t(nh)

nn=1;%round(nh/20);

figure(1)

for i = 1:nn:nh

MQ = [H(i,1) H(i,2); H(i,3) H(i,4)];

MQ=(MQ+MQ')/2;

krug(MQ,0,'g');

hold on;

end;

krug(Q0,0,'k');

krug(Q,0,'k--');

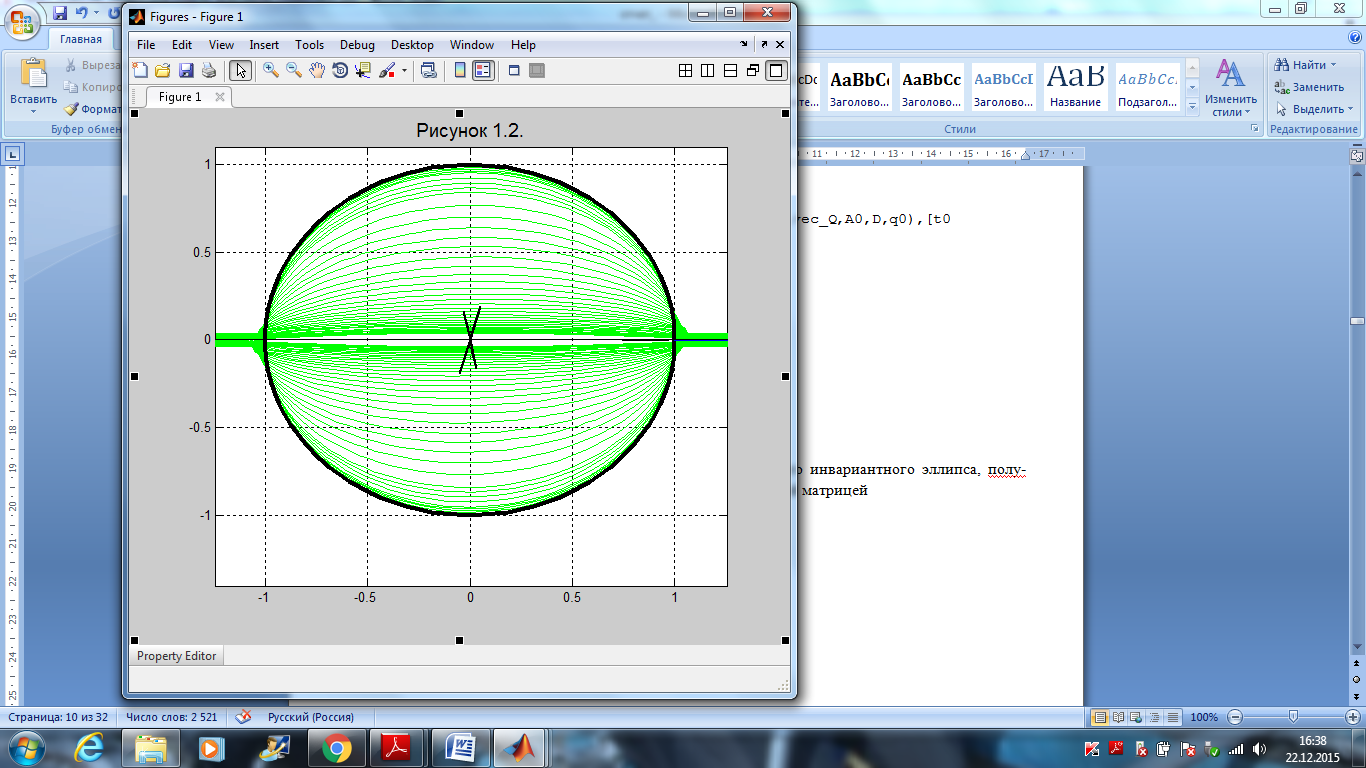
На рисунке 1.2 показаны сечения эволюционирующего инвариантного эллипса, полученные на основе численного решения МСС с начальной матрицей Q=[1 0; 0 1];

Date: 2016-01-20; view: 375; Нарушение авторских прав