Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Четырёхмерная скорость
|
|
В декартовых координатах
В прямоугольной декартовой системе координат[8]:
В то же время 
, поэтому
Таким образом, координаты вектора скорости — это скорости изменения соответствующей координаты материальной точки[8]:
.
В полярных координатах
Скорость в полярных координатах
В цилиндрических координатах 
[8]:
.
носит название поперечной скорости,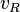 
— радиальной.
В сферических координатах
В сферических координатах 
[8]:
.
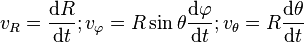Обобщения
Обобщениями понятия скорости является четырёхмерная скорость, или скорость в релятивистской механики, и обобщённая скорость, или скорость в обобщённых координатах[8].
Четырёхмерная скорость
В специальной теории относительности каждому событию ставится в соответствие точка пространства Минковского, три координаты которого представляют собой декартовы координаты трёхмерного евклидова пространства, а четвёртая ― временну́ю коодинату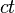 
, где 
― скорость света, 
― время события. Компоненты четырёхмерного вектора скорости связаны с проекциями трёхмерного вектора скорости следующим образом[8]:
Четырёхмерный вектор скорости является времениподобным вектором, то есть лежит внутри светового конуса[8].
Date: 2016-01-20; view: 532; Нарушение авторских прав