Задача Штурма-Лиувилля

Рассмотрим однородное дифференциальное уравнение системы. Для нахождения его общего решения необходимо составить характеристическое уравнение и найти его корни:

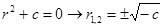
В зависимости от знака константы, структура общего решения будет различаться. При этом для нахождения частных решений необходимо использовать краевые условий . Возможны три ситуации:

а)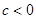

- общее решение: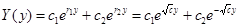

- частное решение: , можно показать, что данная система имеет нетривиальное решение только в случае, если 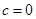, что противоречит условию данной структуры общего решения.

б)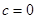

- общее решение: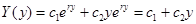

- частное решение: 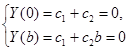и данная система не имеет нетривиальных решений.

в)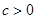

- общее решение: т.к. 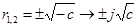, то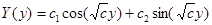

- частное решение: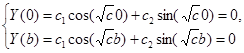

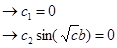
Последнее уравнение обладает бесконечным множеством нетривиальных решений:

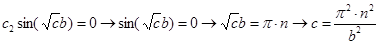где

Отсюда искомая функция 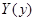запишется в виде:

Непосредственной подстановкой в исходное уравнение можно доказать что данная функция является частным решением для любых значений . Для счетного множества значений , множества собственных чисел и функций запишутся в виде:

(2) ,

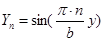
Метод Фурье (продолжение)

Рассмотрим первое уравнение системы (1):

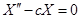
Его общее решение с учетом корней характеристического уравнения () и положительности значений константы () запишется в виде:

(здесь – константы интегрирования)

Для дальнейших построений, воспользуемся одним из граничных условий уравнения (1), а именно однородным условием: 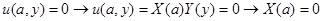. Подставляя в него полученное выше решение, получим:

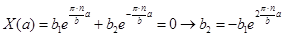
Т.е. формула для запишется следующим образом: 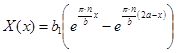. Данное выражение обычно записывают в более удобном виде, приводя к формуле для гиперболического синуса:

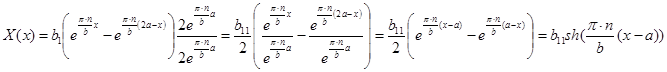
Множество собственных функций в данном случае:

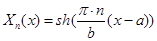
Теперь можно обратиться к общей идеи метода Фурье – к поиску всего многообразия частных решений в виде 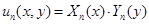. Доказано, что линейная комбинация частных решений также является частным решением, поэтому наиболее «полное» решение исходной задачи представляется следующей зависимостью:

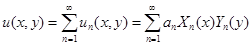
где 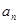- константы, значение которых необходимо определить, используя условия задачи.

В нашем случае однородные граничные условия для и 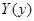использовались для решения задачи Штурма – Лиувилля, поэтому для определения 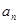используем неоднородное граничное условие: 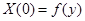. Имеем:

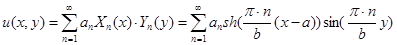
(при этом можно показать, что 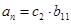). Подставляя данное выражение в граничное условие 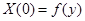, получим:

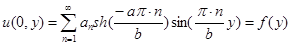
Учитывая выражения для коэффициентов Фурье для тригонометрического ряда (для нечетных функций: ), запишем:

Тем самым мы получили искомый ответ исходной задачи:

,

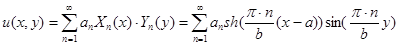где

Для проверки этого решения его необходимо подставить в исходное уравнение, что с учетом наличия рядов является трудоемкой задачей. Для упрощения процедуры, преобразуем исходную задачу, а именно выберем конкретный вид функции : .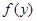

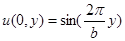Находя коэффициенты 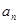, получим: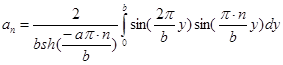

для

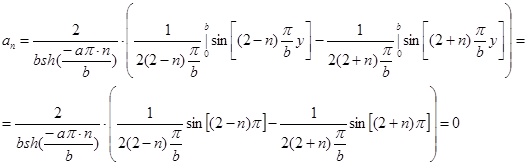
для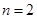

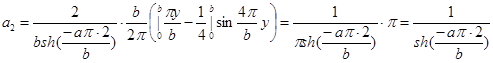
Окончательный результат: можно проверить непосредственно подстановкой в исходное уравнение.

Представленный вывод может быть получен более простым способом - непосредственной анализом «общей» линейной последовательности 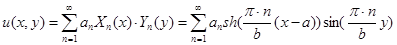по известному (конкретному) граничному условию .

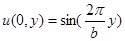Имеем: . Для любых 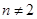нет значений 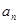приводящих данное выражение в верное тождество. Соответственно для 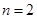получаем:

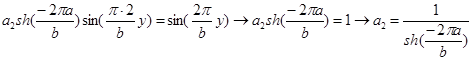
Date: 2016-01-20; view: 1056; Нарушение авторских прав