Понятие задачи

Общее решение уравнения в частных производных представляет собой бесконечное множество функций от независимых переменных. Для того чтобы выделить единственное решение необходимо задать дополнительные условия – временные и/или краевые. Тем самым вводится понятие задача – это уравнения с дополнительными условиями. Примерами задач являются:

а) задачи распространения волн и тепла в бесконечном стержне:

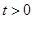
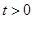
здесь указано, что пространственная координата не имеет ограничений (нет краевых условий), но вводится начальное условие: при функция имеет заданный вид (для гиперболического уравнения – дополнительное условие на скорость функции - в начальный момент). Данного типа задачи с начальными условиями именуются задачами Коши.

Если вышеуказанные процессы рассматривать в ограниченной области пространства, то начальные условия дополняются граничными, тем самым рассматриваются смешанные задачи:

б) задача колебания закрепленной на концах струны:

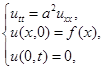
здесь область пространства ограниченна , кроме начального заданы также краевые условия (т.к. струна закреплена, то ее колебания в точках и 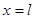в любой момент времени отсутствуют)

в) задача нагрева/охлаждения стержня:

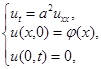
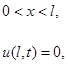
Отметим, что возможны и другие виды граничных условий (в частности производные от функции на концах стержня и т.д.)

Для эллиптических задач (при рассмотрении стационарных явлений) вводятся краевые (граничные) условия, среди которых выделяют три основных:

а) граничное условие I рода (условие Дирихле) - решение эллиптического уравнения ищется в некоторой области пространства при заданном значении на границе этой области , например для уравнения Лапласа:

Пример задачи Дирихле для уравнения Лапласа – распространение температуры/эл. заряда внутри некоторого тела при заданной температуре/потенциале на его поверхности.

б) граничное условие II рода (условие Неймана) - решение эллиптического уравнения ищется в некоторой области пространства при заданном значении на границе этой области внешней нормальной производной искомой функции - :

Пример задачи Неймана для уравнения Лапласа – распространение температуры/эл. заряда внутри некоторого тела при заданном потоке температуры/заряде на его поверхности.

в) граничное условие III рода (условие Робэна) - решение эллиптического уравнения ищется в некоторой области пространства , удовлетворяющее на границе этой области условию , где - некоторые функции:

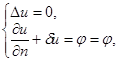
Отметим, что для различных уравнений, описанных в эллиптических задачах, необходимо выполнение дополнительных условий, связанных с физической сутью задач. Так для уравнения Лапласа в задаче Неймана накладывается ограничение: 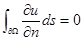- т.е. полный поток через всю поверхность тела должен равняться нулю (входящий поток равен исходящему).

2. Метод Фурье

Одним из наиболее изученных методов решений частных производных II порядка является метод разделения переменных (метод Фурье). Для рассмотрения данного метода воспользуемся следующим примером: дана задача о распределении заряда на прямоугольной пластине в случае, если на левую сторону нанесен потенциал (переменный вдоль стороны)

Данная задача представляет собой задачу Дирихле для эллиптического уравнения Лапласа на плоскости:

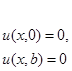
В методе Фурье решение ищется в виде функции с разделенными переменными, в данном случае . При подстановке данной функции в исходное уравнение все частные производные обратятся в обыкновенные:

При этом само уравнение обратится в уравнение с разделенными переменными (в дальнейшем будем опускать обозначения переменных функций):

Непосредственно разделяя переменные, получим:

Так как правая и левая части уравнений зависят от разных переменных, то они равны только в том случае, если являются константой, т.е.

Отсюда можно записать систему из двух обыкновенных дифференциальных уравнений:

(1)

Далее рассматривают решение одного из этих уравнений, учитывая заданные граничные условия. В данном случае возьмем второе уравнение, для которого граничные условия выводятся следующим образом:

для нетривиальных значений

Аналогично:

- т.е. оба граничных условия для данного уравнения однородны.

В итоге получаем обыкновенное однородное дифференциальное уравнение с однородными граничными условиями:

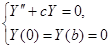
Решение данной системы представляет собой задачу Штурма-Лиувилля. Эта задача связанна с поиском собственных значений (чисел) константы и связанных с ними собственными функциями , при этом доказано, что существует счетное (дискретное) множество этих функций (чисел).

Date: 2016-01-20; view: 391; Нарушение авторских прав