Статистические характеристики СП

Функция распределения вероятности и плотность распределения вероятности дают полное вероятностное описание СП лишь для одного фиксированного момента времени .

Функция распределения вероятности определяется как вероятность того, что в момент времени значение СП не превосходит некоторого заданного значения :

.

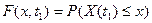Плотность распределения вероятности представляет собой производную от функции распределения вероятности:

.

Произведение представляет собой вероятность попадания значения СП в бесконечно малый интервал в окрестности точки .

Математическое ожидание – среднее значение СП в текущий момент времени, полученное усреднением по всему ансамблю реализаций:

.

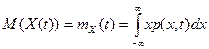Дисперсия характеризует среднюю мощность отклонений СП от его среднего значения:

.

Среднеквадратическое отклонение представляет собой квадратный корень из дисперсии и служит амплитудной мерой разброса значений СП в текущий момент времени относительно математического ожидания:

.

Функция корреляция представляет собой меру связи (корреляции) между сечениями СП, взятыми в произвольные моменты времени и :

,

где - двумерная плотность распределения вероятности, которая описывает двумерную случайную величину , образованную совокупностью двух сечений СП в различные моменты времени и ;

- вероятность того, что реализация СП в момент времени попадет в бесконечно малый интервал шириной в окрестности точки , а в момент времени - в бесконечно малый интервал шириной в окрестности точки .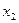

При выражение соответствует определению дисперсии СП.

Чем медленнее убывает функция с ростом интервала между моментами времени и , тем больше промежуток, в течение которого наблюдается статистическая связь между мгновенными значениями СП, и тем медленнее, плавне изменяются во времени его реализации.

Стационарными называют СП, статистические характеристики которых одинаковы во всех временных сечениях. Для стационарного СП функция распределения вероятности, плотность распределения вероятности, математическое ожидание и дисперсия не зависят от времени, а корреляционная функция зависит не от самих моментов времени, а от интервала между ними . По этой причине при записи статистических параметров стационарного СП можно опускать обозначения фиксированных моментов времени: .

Стационарный СП называется эргодическим, если при определении любых его статистических характеристик усреднение по множеству (ансамблю) реализаций эквивалентно усреднению по времени одной, теоретически бесконечно длинной, реализации. Другими словами, если изучаемый процесс является эргодическим, то его реализация достаточной длины является «типичным» представителем статистического ансамбля, и по этой единственной реализации можно определить математическое ожидание, дисперсию и корреляционную функцию СП:

,

,

.

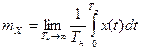где - время наблюдения реализации .

Принято моделировать реальные сигналы эргодическим и стационарным СП.

Спектральная плотность мощности 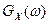представляет собой среднюю мощность СП, приходящуюся на 1 Гц в окрестности заданной частоты . В общем случае спектральную плотность мощности необходимо усреднить по множеству реализаций, т.е. она находится как среднее значение отношения квадрата спектральной плотности к длительности интервала наблюдения. Если ограничиться рассмотрением эргодических процессов, можно считать, что найденная по одной реализации (путем усреднения во времени) спектральная плотность мощности рассматриваемой реализации характеризует весь процесс в целом:

,

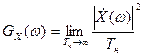где - спектральная плотность рассматриваемой реализации СП , длительность которой ограничена конечным интервалом . Находится с помощью прямого преобразования Фурье.

Date: 2016-02-19; view: 423; Нарушение авторских прав