
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

В 27. Принцип оптимальности и рекуррентные соотношения Беллмана
|
|
Принцип оптимальности был сформулирован Беллманом в 1953г. Сформулируем его так, как было предложено Венцель (несколько отличным образом).
Рассмотрим n-й последний шаг: Sn-1 состояние системы к началу n-ого шага, Sn – конечное состояние, Хn – управление на n-ом шаге, а fn (Sn-1, Xk) – целевая функция (или как еще говорят – выигрыш) n-ого шага.
Согласно принципу оптимальности, Хn нужно выбирать так, чтобы для любых состояний Sn-1 получить максимум (или минимум – ограничимся задачей на максимум – это не принципиально) целевой функции на этом шаге. Каково бы ни было состояние S системы в результате какого-либо шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.
Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого процесса. Поэтому решение на каждом шагу оказывается наилучшим с точки зрения управления в целом.
Рекуррентные соотношения Беллмана. Вместо исходной задачи с фиксированным числом шагов n и начальным состоянием S0 рассмотрим последовательность задач, полагая последовательно n = 1, 2, … при различных S – одношаговую, двухшаговую, и т.д. – используя принцип оптимизации.
На каждом шаге для любого состояния системы Sk-1 решениеХk (управление) нужно выбирать «с оглядкой», так как этот выбор влияет на последующее состояние Sk и дальнейший процесс управления, зависящий от Sk.
Но есть один шаг, последний, который может для любого состояния Sn-1 планировать локально-оптимально, исходя только из соображений этого последнего шага.
Обозначим через  (Sn-1) максимум целевой функции – показателя эффективности n-ого шага при условии, что к началу последнего шага система S была в произвольном состоянии Sn-1, а на последнем шаге управление было оптимальным.
(Sn-1) максимум целевой функции – показателя эффективности n-ого шага при условии, что к началу последнего шага система S была в произвольном состоянии Sn-1, а на последнем шаге управление было оптимальным.
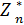 (Sn-1) называется условным максимумом из функции на n-ом шаге. Очевидно, что
(Sn-1) называется условным максимумом из функции на n-ом шаге. Очевидно, что
|
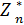 (Sn-1) = max fn (Sn-1, Xk) (1)
(Sn-1) = max fn (Sn-1, Xk) (1)
Максимизация ведется по всем допустимым управлениям Хn.
Решение Хn, при котором достигается 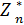 (Sn-1), также зависит от Sn-1 и называется условным оптимальным управлением на n-ом шаге. Оно обозначается
(Sn-1), также зависит от Sn-1 и называется условным оптимальным управлением на n-ом шаге. Оно обозначается  (Sn-1).
(Sn-1).
Решив одномерную задачу локальной оптимизации по уравнению (1), найдем для всех возможных состояний Sn-1 две функции 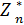 (Sn-1) и
(Sn-1) и  (Sn-1).
(Sn-1).
Рассмотрим теперь двух шаговую задачу: присоединим к n-ому шагу (n-1) ша.
Для любых состояний Sn-2, произвольных уравнений Хn-1 и оптимальном уравнении на n-ом шаге значение целевой функции на двух последних шагах равно
fn-1 (Sn-2, Xn-1) + 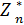 (Sn-1) (2)
(Sn-1) (2)
согласно принципу оптимальности для любого Sn-2 решение нужно выбирать так, чтобы оно вместе с оптимальным управлением на последнем n-ом шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно найти максимум выражения (2) по всем допустимым управлениям Xn-1. Максимум этой суммы зависит от Sn-2, обозначается
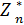 (Sn-2) и называется максимум целевой функции при оптимальном управлении на двух последних шагах.
(Sn-2) и называется максимум целевой функции при оптимальном управлении на двух последних шагах.
Соотношение управления Xn-1 на (n-1) – шаге обозначается 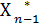 (Sn-2) и называется условным оптимальным управлением на (n-1) – шаге.
(Sn-2) и называется условным оптимальным управлением на (n-1) – шаге.
|
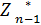 (Sn-2) = max {fn-1 (Sn-2, Xn-1) +
(Sn-2) = max {fn-1 (Sn-2, Xn-1) + 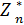 (Sn-1)} (3)
(Sn-1)} (3)
Следует обратить внимание на то, что выражение в фигурных скобках зависит только от Sn-2 и Xn-1, т.к. Sn-1 можно найти из уравнения состояний при k=n-1
Sn-1 = φn-1 (Sn-2, Xn-1)
В результате максимизации по переменной Xn-1 согласно уравнению (3) вновь получаем две функции:
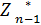 (Sn-2) и
(Sn-2) и 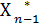 (Sn-2)
(Sn-2)
Далее рассматривается трех шаговая задача: к двум последним шагам присоединяется (n-2) шаг и т.д. Выражение (3) можно обобщить следующим образом.
Обозначим через  (Sk-1) условный максимум целевой функции при оптимальном управлении на n-k+1 шагах, при условии, что к началу k-ого шага система находилась в состоянии Sk-1, т.е. k=n-1, n-2, …., 2, 1; если k=n-1, то
(Sk-1) условный максимум целевой функции при оптимальном управлении на n-k+1 шагах, при условии, что к началу k-ого шага система находилась в состоянии Sk-1, т.е. k=n-1, n-2, …., 2, 1; если k=n-1, то
1. n-k+1 = n-n+1+1=2 – тогда  (Sk-1) – условный максимум целевой функции при оптимальном управлении на двух последних шагах
(Sk-1) – условный максимум целевой функции при оптимальном управлении на двух последних шагах
2. k=n-2 n-n+2+1 = 3 – на трех последних шагах
3. k=1 n-1+1 = n - на n последних шагах.
Итак по аналогии: для любых состояний Sk-1, произвольном управлении Хk и оптимальном уравнении на последующих (n-k) – шагах значение целевой функции на последних (n-k+1) – шагах равно
fk (Sk-1, Xk) + 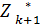 (Sk)
(Sk)
Максимум этой суммы зависит от Sk-1 и обозначается  (Sk-1), т.е.
(Sk-1), т.е.
|
 (Sk-1) = max {fk (Sk-1, Xk) +
(Sk-1) = max {fk (Sk-1, Xk) + 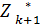 (Sk)} (**)
(Sk)} (**)
k=n-1, n-2, ….., 2, 1
управление Xk на k-ом шаге, при котором достигается максимум (**)
при k=n
|
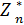 (Sn-1) = max fn (Sn-1, Xn) - это тоже иногда включают в (**)
(Sn-1) = max fn (Sn-1, Xn) - это тоже иногда включают в (**)
 (Sk-1) = max {fk (Sk-1, Xk) +
(Sk-1) = max {fk (Sk-1, Xk) +  (Sk)} (4)
(Sk)} (4)
k=n-1, n-2, ….., 2, 1
Управление Xk на k-ом шаге, при котором достигается максимум (4), обозначается  (Sk-1) и называется условным оптимальным управлением на k-ом шаге (в правую часть вместо Sk нужно подставить Sk = φk (Sk-1, Xk), найденное из уравнений состояний.
(Sk-1) и называется условным оптимальным управлением на k-ом шаге (в правую часть вместо Sk нужно подставить Sk = φk (Sk-1, Xk), найденное из уравнений состояний.
Уравнения (4) называются рекуррентными соотношениями Беллмана. Эти соотношения позволяют найти предыдущее значение функции, зная последующее. Если из (1) найти 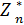 (Sn-1), то при k=n-1 из (4) можно определить, решив задачу максимизации для всех возможных значений Sn-2, выражение для
(Sn-1), то при k=n-1 из (4) можно определить, решив задачу максимизации для всех возможных значений Sn-2, выражение для 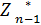 (Sn-2) и соответствующее управление
(Sn-2) и соответствующее управление 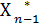 (Sn-2). Далее, зная
(Sn-2). Далее, зная 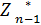 (Sn-2), по аналогии
(Sn-2), по аналогии 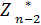 (Sn-3) и
(Sn-3) и  (Sn-3) (k=n-2).
(Sn-3) (k=n-2).
Процесс решения уравнений (1) и (4) называется условной оптимизацией.
В результате условной оптимизации получаются две последовательности
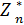 (Sn-1),
(Sn-1), 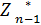 (Sn-2), ……,
(Sn-2), ……,  (S2),
(S2),  (S0) – условные максимумы целевой функции на последнем, на двух последних и т.д., наконец, на n- последних шагах.
(S0) – условные максимумы целевой функции на последнем, на двух последних и т.д., наконец, на n- последних шагах.
При этом набор значений для разных возможных значений Sn-1
 (Sn-1),
(Sn-1), 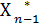 (Sn-2), ……,
(Sn-2), ……,  (S2),
(S2), 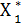 (S0) – условные оптимальные управления на n-ом, (n-1)-м, …, 1-м шагах.
(S0) – условные оптимальные управления на n-ом, (n-1)-м, …, 1-м шагах.
Используя эти последовательности, можно найти решение задачи динамического программирования при данных n и S0. По определению  (S0) – условный максимум целевой функции за n шагов при условии, что к началу первого шага система была в состоянии S0, т.е. Zmax=
(S0) – условный максимум целевой функции за n шагов при условии, что к началу первого шага система была в состоянии S0, т.е. Zmax=  (S0)
(S0)
Далее следует последовательность условных оптимальных управлений и уравнений состояний.
При фиксированном S0 получаем 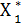 =
= 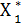 (S0).
(S0).
Далее из уравнений состояний находим  = φ1 (S0,
= φ1 (S0, 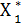 ), через
), через 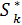 здесь обязательно состояние системы после k-ого шага.
здесь обязательно состояние системы после k-ого шага.
В последовательность условных оптимальных управлений
 =
=  (S1) и т.д. по цепочке:
(S1) и т.д. по цепочке:


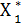 =
= 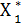 (S0)
(S0)  = φ1 (S0,
= φ1 (S0, 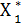 ) =>
) =>  =
=  (
( )
)  = φ2 (
= φ2 ( ,
,  ) =>
) =>


 =
=  (
( ) …..
) …..  = φn-1 (
= φn-1 ( ,
, 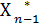 ) =>
) =>  =
=  (
( )
)
 означает уравнения состояния, а => - последовательность условных оптимальных управлений.
означает уравнения состояния, а => - последовательность условных оптимальных управлений.
В результате получаем оптимальное решение задачи динамического программирования:
 =
= 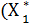 ,
,  )
)
Date: 2016-02-19; view: 492; Нарушение авторских прав