Метрический тензор Римана: новая теорема Пифагора

Риману понадобилось несколько месяцев, чтобы оправиться от последствий нервного срыва. Его доклад, наконец прочитанный в 1854 г., приняли с воодушевлением. В ретроспективе это был, бесспорно, один из наиболее выдающихся публичных докладов в истории математики. По Европе быстро распространилось известие, что Риман решительно сбросил оковы евклидовой геометрии, которой математики подчинялись на протяжении двух тысячелетий. О докладе вскоре узнали во всех центрах образования Европы, вклад Римана в математику приветствовали повсюду в научных кругах. Доклад Римана перевели на несколько языков, он произвел фурор в математике. К евклидовой геометрии раз и навсегда перестали относиться так, как прежде.

Суть выдающегося труда Римана, как и суть многих величайших работ в области физики и математики, уловить довольно просто. Риман начал со знаменитой теоремы Пифагора, одного из важнейших достижений древнегреческих математиков. Эта теорема устанавливает соотношения между длинами сторон прямоугольного треугольника. Согласно ей, сумма квадратов коротких сторон, катетов, равна квадрату длинной стороны, гипотенузы; если а и b — длины катетов, ac — длина гипотенузы, тогда а2 + Ь2 = с2. (Естественно, теорема Пифагора лежит в основе всей архитектуры; все сооружения на планете построены с ее учетом.)

Эту теорему легко сформулировать для трехмерного пространства. Она гласит, что сумма квадратов трех смежных сторон куба равна квадрату его диагонали; или если а, Ь и с — стороны куба, ad — его диагональ, тогда а2 + b2 + с2 = d2 (рис. 2.1).

Рис. 2.1. Длину диагонали куба дает трехмерный вариант теоремы Пифагора: a2 + Ь2 + c2 = d2. Простого добавления новых переменных в теорему Пифагора достаточно, чтобы записать формулу для диагонали гиперкуба в N-мерном пространстве. Таким образом, несмотря на сложность визуализации высших измерений, представить N-мерность математически довольно просто.

Теперь так же просто можно сформулировать ту же теорему для N -мерного пространства. Представим себе N -мерный куб. Если а, Ь, с… — длины сторон «гиперкуба», а z — длина его диагонали, тогда а2 + Ь2 + с2 + d2 +… = z2. Примечательный момент: хотя наш мозг не в состоянии представить N -мерный куб, формулу для его сторон и диагонали записать несложно. (Это типичная особенность работы с гиперпространством. С математической, точки зрения манипулировать N -мерным пространством не труднее, чем трехмерным пространством. Поразительно, как на простом листе бумаги можно математически описать свойства многомерных объектов, которые не в силах вообразить наш мозг.)

Затем Риман записал эти уравнения для пространств с произвольным количеством измерений. Эти пространства могут быть либо плоскими, либо искривленными. К плоским применяются обычные аксиомы Евклида: кратчайшее расстояние между двумя точками — прямая, параллельные линии никогда не пересекаются, сумма внутренних углов треугольника составляет 180°. Вместе с тем Риман обнаружил, что поверхности могут иметь «положительную кривизну», как поверхность сферы, где параллельные всегда пересекаются и сумма углов треугольника может быть больше 180°. Бывают и поверхности с «отрицательной кривизной»: например, седлообразные или воронкообразные. На этих поверхностях сумма углов треугольника меньше 180°. Если взять линию и точку вне этой линии, то через такую точку можно провести бесконечное множество линий, параллельных данной (рис. 2.2).

Рис. 2.2. Плоскость имеет нулевую кривизну. Согласно евклидовой геометрии сумма углов треугольника равна 180°, параллельные не пересекаются. В неевклидовой геометрии сфера имеет положительную кривизну. Сумма углов треугольника превышает 180°, параллельные линии всегда пересекаются. (К параллельным линиям относятся дуги, центры которых совпадают с центром сферы. Широтные линии в эту категорию не входят.) У седлообразной поверхности отрицательная кривизна. Сумма углов треугольника меньше 180°. Через конкретную точку можно провести бесконечное множество линий, параллельных данной.

Целью Римана было ввести в математику новый элемент, позволяющий описывать все поверхности независимо от их сложности. Как и следовало ожидать, эта цель побудила его обратиться к фарадеевой концепции поля.

Как мы помним, поле Фарадея представляло собой подобие крестьянского, занимающего двумерный участок пространства. Фарадеево поле занимает часть трехмерного пространства; любой точке этого пространства мы присваиваем ряд параметров, описывающих магнитное или электрическое взаимодействие в этой точке. Идея Римана заключалась в том, чтобы присвоить каждой точке пространства ряд параметров, которые описывали бы степень его деформации или кривизны.

К примеру, для обычной двумерной поверхности Риман вводил набор из трех параметров для каждой точки, полностью описывающих искривление этой поверхности. Риман обнаружил, что в четырех пространственных измерениях для описания свойств каждой точки требуется набор из десяти параметров. Каким бы «скомканным» или искривленным ни было пространство, этих десяти параметров для каждой точки оказывалось достаточно, чтобы зашифровать всю информацию о данном пространстве. Обозначим эти десять параметров как g11, g12, g13, и т. д. (при анализе четырехмерного пространства нижний индекс меняется от единицы до четырех). В этом случае риманов набор из десяти параметров можно симметрично расположить, как показано на рис. 2.3^[15]. (Несмотря на то что компонентов всего 16, g12 = g21, g13 = g31 и т. д., т. e. в действительности независимых компонентов только десять.) В настоящее время этот набор параметров называется римановым метрическим тензором. Грубо говоря, чем больше значение метрического тензора, тем сильнее скомкан лист. Как бы ни был смят лист бумаги, метрический тензор дает нам простое средство измерения его кривизны в любой точке. Если же мы полностью расправим скомканный лист, сделаем его плоским, то снова вернемся к теореме Пифагора.

Рис. 2.3. Метрический тензор Римана содержит всю информацию, необходимую для математического описания изогнутого N-мерного пространства. Для каждой точки четырехмерного пространства требуется метрический тензор с 16 параметрами. Эти числа можно расположить в виде квадратной матрицы (из этих параметров шесть на самом деле избыточны, следовательно, в метрический тензор входит десять независимых параметров).

Метрический тензор позволил Риману построить эффективный аппарат для описания пространств с любым количеством измерений и произвольной кривизной. К своему изумлению, Риман обнаружил, что все эти пространства четко определены и логически последовательны. Ранее считалось, что при исследовании запретного мира высших измерений непреодолимые противоречия неизбежны. Но, как ни странно, Риман не заметил ни одного. Напротив, переход к N -мерным пространствам оказался почти пустяковым делом. Метрический тензор приобрел сходство с шахматной доской размером NxN клеток. Это обстоятельство приобретет глубокий физический смысл в следующих главах, когда мы перейдем к объединению всех сил.

(Как мы убедимся, секрет объединения кроется в расширении метрического тензора Римана до N -мерного пространства с последующим его нарезанием на прямоугольные части. Каждый прямоугольник соответствует одному взаимодействию. В этом случае можно описывать различные силы природы, размещая их в метрическом тензоре, как элементы в головоломке. Таково математическое выражение принципа, согласно которому многомерное пространство объединяет законы природы так, что для их объединения «хватает места» в N -мерном пространстве. Точнее, для объединения сил природы «достаточно места» в метрическом тензоре Римана.)

Риман предсказал еще одно направление развития физики: он первым заговорил о многосвязных пространствах, или «червоточинах». Для наглядного представления этой концепции возьмите два листа бумаги, положите один на другой. Сделайте ножницами короткий разрез на каждом листе. Потом склейте листы друг с другом вдоль разрезов (рис. 2.4). (Топологически получается то же самое, что и на рис. 1.1, только горловина «червоточины» имеет нулевую длину.)

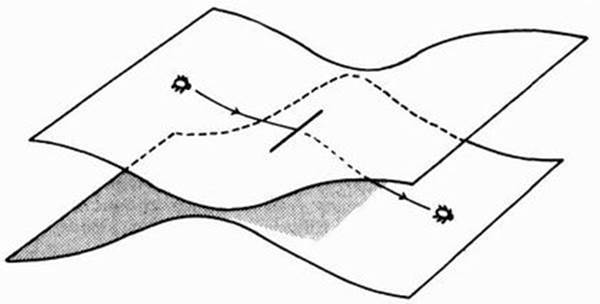
Рис. 2.4. Разрез Римана и два листа, соединенных друг с другом по одной линии. Если обойти разрез, мы останемся в пределах одного и того же пространства. Если пройти в разрез, мы перейдем с одного листа на другой. Таковы многосвязные пространства.

Жучок, живущий на верхнем листе, может когда-нибудь случайно заползти в разрез и очутиться на нижнем листе. И озадачиться, так как все вокруг изменится. После многочисленных экспериментов жучок наверняка поймет, что можно вернуться в привычный мир, если проползти через разрез в обратном направлении. Стоит только сделать это — и мир станет обычным, но любые попытки пройти через разрез в надежде сократить путь чреваты проблемами.

Разрез Римана — пример «червоточины» (с нулевой длиной), соединяющей два пространства. Римановы разрезы с успехом применил математик Льюис Кэрролл в книге «Алиса в Зазеркалье». Зеркало — это и есть риманов разрез, соединяющий Англию и Страну чудес. Сегодня римановы разрезы сохранились в двух видах. Во-первых, о них упоминают в учебных курсах математики всего мира применительно к конформному отображению или теории электростатики.

Во-вторых, римановы разрезы фигурируют в сериале «Сумеречная зона» (следует отметить, что сам Риман никогда не рассматривал эти разрезы как средство перемещения между вселенными).

Date: 2016-02-19; view: 841; Нарушение авторских прав