Список использованных источников. 1. Гидравлика, гидромашины и гидропневмопривод: учеб

1. Гидравлика, гидромашины и гидропневмопривод: учеб. пособие для студ. высш. учеб. заведений / Т. В. Артемьева, Т. М. Лысенко, А. Н. Румянцева, С. П. Стесин. — М.: Издательский центр «Академия», 2005. — 336 с.

2. Гидравлика: учебник для студ. высш. учеб. заведений / Н. Н. Лапшев. — 2-е изд., испр. — М.: Издательский центр «Академия», 2008. - 272 с.

3. Основы гидравлики и теплотехники: учебник для студ. сред. проф. образования / О. Н. Брюханов, А. Т. Мелик-Аракелян, В. И. Коробко. — 3-е изд., стер. - М.: Издательский центр «Академия», 2008. — 240 с.

4. Сборник задач по основам гидравлики и теплотехники: учеб. пособие для техникумов. - 2-е изд., перераб. и доп. — М.: Энергия, 1979. — 240 е., ил.

Ответ: Q=0,0128 м³/с.

Средняя скорость в живом сечении может быть определена из формулы

(2.29)

Основными уравнениями, позволяющими решать простейшие задачи о движении жидкости, являются уравнение расхода (неразрывности) и уравнение Бернулли.

Уравнение расхода представляет собой условие сплошности потока несжимаемой жидкости или, что то же самое, равенство объемных расходов в каких-то двух живых сечениях этого потока, например 1 и 2, т.е. Q₁=Q₂ или u₁ω₁= u₂ω₂- Отсюда следует, что:

(2.30)

Для сжимаемой жидкости и газов уравнение неразрывности имеет

вид:

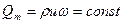(2.31)

2.3.2 Уравнение Д. Бернулли без учета потерь энергии

Уравнение Д. Бернулли для потока жидкости без учета потерь энергии, т.е. для невязкой жидкости, составленное для двух расчетных сечений 1-1 и 2-2 относительно произвольной горизонтальной плоскости сравнения, записывается в следующем виде:

(2.32)

где а - коэффициент, учитывающий неравномерность распределения скоростей по сечению потока (коэффициент кинетической энергии).

С физической точки зрения уравнение Д. Бернулли выражает закон сохранения энергии в потоке движущейся жидкости. Левая и правая части этого уравнения представляют собой сумму двух видов удельной энергии:

потенциальной, состоящей из энергии положения z и энергии давления , и кинетической . Коэффициент кинетической энергии α при движении невязкой жидкости с достаточной степенью точности может быть принят равным единице.

С геометрической точки зрения уравнение Д. Бернулли представляет

собой уравнение напоров. Гидродинамический напор H_d состоит из суммы пьезометрического напора и скоростного напора .

В большинстве случаев при расчете движения жидкости совместно с уравнением Д. Бернулли применяется уравнение неразрывности (сплошности) потока.

2.3.3 Режимы движения жидкости. Гидравлические потери.

Движение вязкой (реальной) жидкости сопровождается затратами энергии на преодоление сопротивлений движению. Эти потери энергии определяются по-разному при различных режимах движения. Существует два режима движения жидкости: ламинарный и турбулентный. При ламинарном режиме жидкость движемся слоями, а при турбулентном режиме движения наблюдается беспорядочное перемешивание частиц жидкости.

Режим движения жидкости характеризуется числом Рейнольдса Re, которое в общем случае определяется по формуле

(2.33)

Для напорного движения в круглых трубах применяется формула

(2.34)

где υ - средняя в сечении скорость движения, м/с;

R - гидравлический радиус, м;

D - диаметр трубы, м;

v - кинематический коэффициент вязкости жидкости, м²/с.

Если число Рейнольдса брлыне некоторого критического значения (Re>Re_кp), то поток движется при турбулентном режиме, а при числах Рейнольдса Re<Re_кp устанавливается ламинарный режим.

Для круглых напорных труб принимается Re_кp=2300 и Re_кp=580 для труб иного сечения. Для безнапорных потоков Re_кp=300÷500.

Значения кинематического коэффициента вязкости v для некоторых жидкостей приведены в таблице 2.1

Таблица 2.1 — Значения кинематического коэффициента вязкости v

Определим величину пьезометрического напора в сечении 1-1:

Определим величину пьезометрического напора в сечении 2-2. Здесь

Далее определим величину пьезометрического напора в сечении 3-3:

В сечении 4-4 р₄=0 и

Откладывая полученные значения величин пьезометрических напоров в каждом сечении от плоскости сравнения , строим пьезометрическую линию.

Поскольку напор в трубопроводе постоянного сечения равномерный, напорная линия будет параллельна пьезометрической и расположится выше последней на величину:

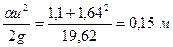
Так как , то

Учитывая, что 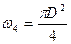, и решив последнее уравнение относительно искомого расхода, получаем

В данном случае сумма коэффициентов потерь местных сопротивлений складывается из коэффициента потерь на входе в трубу и коэффициента потерь в вентиле диаметром D=0,1 м при полном открытии . Таким образом с учетом потерь по длине

Подставляя известные величины в формулу для расхода, находим, что

Для построения пьезометрической линии находим зависимость, по которой можно определить величину пьезометрического напора в любом сечении трубопровода. Для этого составим уравнение Бернулли для сечения 0-0 и любого сечения трубопровода х-х относительно плоскости сравнения

Так как величина пьезометрического напора зависит от манометрического давления, то в дальнейшем во всех сечениях будем рассматривать только манометрическое давление. В связи с этим р₀=0 и

Потери напора по длине в общем случае определяются по формуле Дарси - Вейсбаха

(2.35)

где λ - гидравлический коэффициент трения (коэффициент Дарси);

I - длина расчетного участка трубы;

D - диаметр трубы.

При ламинарном режиме движения гидравлический коэффициент трения зависит от числа Рейнольдса Re и для круглых труб определяется по формуле

(2.36)

При турбулентном режиме движения различают три области гидравлических сопротивлений:

1) Область гидравлически гладких труб при числе Рейнольдса Re = 2320 ÷ 10 · (здесь ∆_экв - эквивалентная шероховатость);

2) Переходная область сопротивлений при Re=(10÷500) ;

3) Область гидравлически шероховатых труб (или квадратичная область) при Re > 500

Эквивалентная шероховатость ∆_экв, мм, для труб имеет следующие значения:

Таблица 2.2 — Значения эквивалентной шероховатости ∆_экв

В области гидравлически гладких труб гидравлический коэффициент трения λ может быть определен по формуле Блазиуса:

(2.37)

Для полиэтиленовых водопроводных труб в области гидравлически гладких труб, также применяется формула Ф.А. Шевелева

(2.38)

В переходной области сопротивления применяются: формула А.Д. Альтшуля

(2.39)

и для водопроводных труб формула Ф.А. Шевелева

(2.40)

где значения коэффициентов m, п и f принимаются по таблице 2.3.

Таблица 2.3 - Значения коэффициентов m, п и f для расчета гидравлического коэффициента трения X по формуле Ф.А. Шевелева

В области гидравлически шероховатых труб коэффициент гидравлического трения X может быть определен по формуле Прандтля

(2.41)

или формуле Б.Л. Шифринсона

(2.42)

Для водопроводных труб применяется формула Ф.А. Шевелева

Подставляем значения коэффициента сопротивления при внезапном сужении трубы и скорости жидкости за местным сопротивление в уравнение (1):

Ответ: h_м=7,1·10^{-5 м.}

Date: 2016-02-19; view: 839; Нарушение авторских прав