The Mean Value Theorem

If f(x) is continuous on [a,b], then there exists

.

To calculate the definite integral when you can find the indefinite integral, you can use the Newton-Leibniz formula:

.

Problem 5. Calculate the definite integral: .

Solution. This integral can bring to the tabular integral using the method of summing up under the sign of the differential: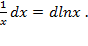

.

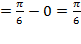Problem 6. Calculate the definite integral: .

Solution. We apply the method of integration by parts: .

Suppose

According to the formula of integration by parts, we find:

Problem 7. Calculate the area of the figure bounded by lines: .

Solution. Area under the graph. Suppose, that there is continuous nonnegative function

, then the area of a region with a curved boundary, bounded by the line and straight lines x=a, x=b and x-axis, is defined by the formula:

.

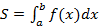If a figure is contained between two lines, then the area is defined as the difference

.

Determine the point of intersection of these given lines. For this it is necessary to solve the system of equations: . This implies:

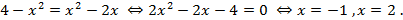
The abscissas of the points of intersection are the limits of integration, that is

According to the formula we find:

Date: 2016-02-19; view: 427; Нарушение авторских прав