Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Table of basic integrals
|
|
1. 
2. 
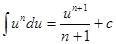
3. 
4. 
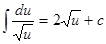
5. 
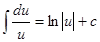
6. 
7. 
8. 
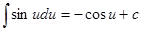
9. 
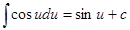
10. 
11. 
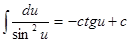
12. 
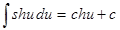
13. 
14. 
15. 
16. 
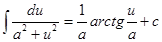
17. 
18. 
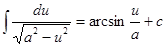
19. 
20. 
21. 
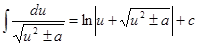
Direct integration is called the evaluation of indefinite integrals by bringing them to the tabulated integrals using the basic properties.
Problem 3. Find the indefinite integral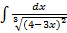 
and the result of integration verify by the differentiation.
Solution. We apply the method of direct integration.
.
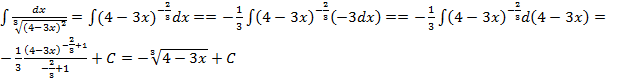Verification. 
.
We got the integrand, hence the integral is found correctly.
Problem 4. Find indefinite integrals:
4.1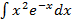 
4.2 
Solution. 4.1 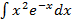. We apply the method of integration by parts. The formula of integration by parts is as follows:
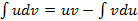(1)
Remark 1. From the considered integral function u and expression dv are chosen so that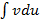 
is simpler than the original integral.
Remark 2. We can find integrals of functions of the forms: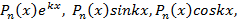 
by integrating by parts: take multiplier 
as u and use formula (1) n times.
Suppose,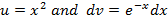 
, then 
.
According to the formula (1) we find:
.
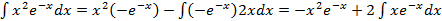The last integral again integrate by parts. Suppose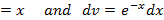 
, then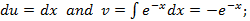 
.
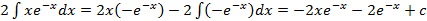Finally, we have
.
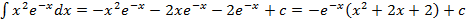Solution. 4.2 . We apply also the method of integration by parts. Suppose
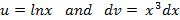, then 
.
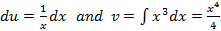According to the formula (1) we find:
.
Date: 2016-02-19; view: 422; Нарушение авторских прав