Потенциальная энергия гравитационного взаимодействия

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами т и М,находящихся на расстоянии r одна от другой, равна

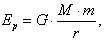(11)

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е_p = 0) принят при r = ∞. Потенциальная энергия гравитационного взаимодействия тела массой т с Землей,где h – высота тела над поверхностью Земли, М ₃– масса Земли, R ₃ – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

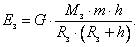(12)

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой т с Землей для малых высот h (h «R ₃)равна

Е_p = m∙g∙h,

где 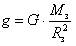– модуль ускорения свободного падения вблизи поверхности Земли.

Потенциальная энергия упруго деформированного тела

Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x ₁до конечного значения x ₂(рис. 4, б, в).

Рис. 4.

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т. к. сила упругости линейно зависит от x) и умножить на модуль перемещения:

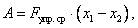(13)

где Отсюда

или

(14)

Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:

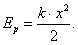(15)

Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:

А = –(Е_{р 2} – Е_{р 1}). (16)

Если x ₂ = 0 и x ₁ = х, то, как видно из формул (14) и (15),

Е_р = А.

Тогда физический смысл потенциальной энергии деформированного тела

потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Механическая работа - физическая величина, равная произведению модуля силы на модуль перемещения и косинус угла между нимиA=Fscosα (см. рис.). Работа - величина скалярная (число, не вектор). Измеряется работа в джоулях (Дж). 1 Дж - это работа, совершаемая силой в 1 Н на перемещение 1 м. В зависимости от направлений векторов силы (F) и перемещения (S) механическая работа может быть положительной, отрицательной или равной нулю. Например, если векторы 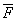и перпендикулярны, то cos900 = 0 и A = 0. Мощность машины или механизма - это отношение совершенной работы ко времени, в течение которого она совершена 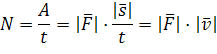. Измеряется мощность в ваттах (Вт), 1 Вт = 1 Дж/с. Простые механизмы: наклонная плоскость, рычаг, блок. Их действие подчиняется«золотому правилу механики»: во сколько раз выигрываем в силе, во столько же раз проигрываем в перемещении. (На практике совершаемая с помощью механизма полная работа всегда несколько больше полезной. Часть работы совершается против силы трения в механизме и перемещения его отдельных частей. Например, применяя подвижный блок, приходится дополнительно совершать работу по поднятию самого блока, веревки и по преодолению силы трения в оси блока. Поэтому для любого механизма полезная работа (AП) всегда меньше, чем полная, затраченная (AЗ). По этой причине КПД = AП/AЗ• 100% любого механизма не может быть больше или хотя бы равен 100%).

Мощность - Мощностью N называют величину, равную отношению работы А к промежутку времени t, в течение которого эта работа была совершена:

N=A/t (3.11)

Из формулы (3.11) следует, что в СИ единицей мощности яв-ляется 1 Дж/с (джоуль в секунду). Эту единицу иначе называют ватт (Вт), 1 Вт= 1 Дж/с.

Связь между мощностью и скоростью при равномерном движении найдем, подставив (3.10) в (3.11):

N=Fvcosa.

(Эта формула справедлива и для переменного движения, если под N понимать мгновенную мощность, а под V - мгновенную скорость). Если направление силы совпадает с направлением перемещения, то cosa=1 и N=Fv. Из последней формулы следует, что

F=N/v и v=N/F.

Из этих формул видно, что при постоянной мощности двигателя скорость движения обратно пропорциональна силе тяги и наоборот. На этом основан принцип действия коробки скоростей (коробки перемены передач) различных транспортных средств.

Консервативными называются силы, работа которых не зависит от формы траектории, а определяется только положением её начальной и конечной точек. К классу консервативных относятся, например, гравитационные силы, упругие, силы электростатического взаимодействия. Вычислим, например, работу, которую совершает сила тяжести при переходах частицы разными путями из положения 1 в положение 2 (рис. 6.2). Если этот переход произошёл по вертикали, то работа силы 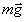: . (6.11) Теперь пусть та же частица переместится из 1 в 2 по пути 1-1’-2. Здесь промежуточная точка 1’ находится на высоте h2. Рис. 6.2 Полная работа будет складываться из работ силы тяжести на участках 1-1’ и 1’-2: . Работа силы тяжести на горизонтальном участке 1’-2 равна нулю, так как здесь вектор силы нормален перемещению. Мы вновь получили прежний результат, свидетельствующий о том, что работа силы тяжести не зависит от формы траектории. Этот вывод легко обобщается и на случай произвольной криволинейной траектории, соединяющей начальную и конечную точки пути. Гравитационная сила, сила упругости, кулоновская сила электростатического взаимодействия относятся к так называемым центральным силам. Центральными называются силы, направленные к одной и той же точке (либо от неё). Эта точка называется силовым центром. Величина центральной силы зависит только от расстояния до силового центра r (рис. 6.3). Рис. 6.3 Покажем, что все центральные силы консервативны. Вычислим работу центральной силы на участке 1-2 произвольной траектории (рис. 6.3). Элементарная работа силы на участке : 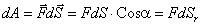. Здесь dSr = dSCosα — проекция вектора перемещения на направление силы (или r). Эта проекция представляет собой изменение расстояния dr до силового центра. Значит: dA = F(r)dr. Работа на конечном пути: . Так как по определению величина центральной силы есть функция только расстояния r, то значение определённого интеграла будет зависеть только от величин r1 и r2, и не будет зависеть от формы траектории. Можно дать иное определение консервативной силы. Рассмотрим перемещение частицы из положения 1 в положение 3 под действием консервативной силы 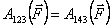(рис. 6.4). Рис. 6.4 Работа, совершаемая при этом силой , не зависит формы от траектории, то есть 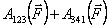. Теперь вычислим работу этой же силы на замкнутом пути 1-2-3-4-1. 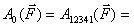понятно, что её можно представить суммой работ на участках 1-2-3 и 3-4-1 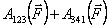При этом 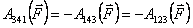. Отсюда можно заключить, что работа консервативной силы по любому замкнутому пути равна нулю 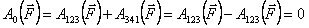. Силы, работа которых на замкнутом пути не равна нулю, называются неконсервативными. К числу таких сил относятся, например, сила трения и сила вязкого сопротивления. Легко понять, что при движении частицы по замкнутому контуру работа подобных сил будет отрицательной.

Date: 2016-02-19; view: 1396; Нарушение авторских прав