Число ребер графа

Когда мы ввели понятие графа как своего рода списка уже проведенных игр, мы предполагали, что каждые две команды играют друг с другом, самое большее, по одному разу. Может, однако, случиться, что каждые две команды играют между собой и по нескольку игр, как это бывает, например, в футболе. Мы можем отразить это на графе, соединяя соответствующие пары вершин несколькими ребрами (рис. 15). В этом случае говорят, что граф имеет кратные ребра.

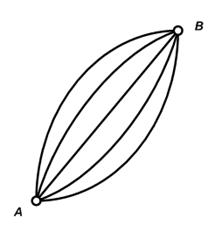
Рис. 15. Граф с 5 кратными ребрами

Вместо того чтобы на самом деле проводить несколько ребер между одними и теми же вершинами А и В, можно провести всего одно ребро, приписав ему кратность, показывающую сколько раз надо считать это ребро (рис. 16). На карте дорог, конечно, проводят каждую дорогу в отдельности.

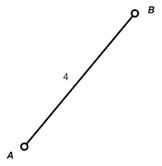
Рис. 16. Экономичное изображение графа с ребром кратности 4

В каждой неизолированной вершине А некоторого графа G имеется одно или несколько ребер, для которых А служит концом; все эти ребра называются инцидентными вершине А. Число таких ребер обычно обозначают через р(А) и называют степенью вершины А.

Так, для графа G, изображенного на рис. 1, степени вершин таковы:

p(A)=p(B)=p(D)=p(E)= 3; p(F)= 4, р(С)= 2.

Довольно часто приходится находить число ребер графа. Их можно, конечно, пересчитать непосредственно, но проще сосчитать число ребер в каждой вершине отдельно и сложить все эти числа. При этом каждое ребро будет сосчитано дважды — соответственно двум вершинам, которые оно соединяет, поэтому общее число ребер графа будет равно половине этой суммы. Так, например, число ребер графа G с рис. 1 равно

½[ р (А)+ р (В)+р (С)+ р (В)+ р(Е)+ р (Р) ] = 9.

Чтобы сформулировать соответствующий результат в общем виде, предположим, что некоторый граф G имеет n вершин

А₁, А₂..., А_n,

степени которых соответственно равны

р(А₁), р(А₂),..., р(А_n).

Тогда число N ребер графа G, как показывает наше рассуждение, равно

N =1/2[ р(А₁)+р(А₂)+ … +р(А_n) ]. (1)

Из этой формулы видно, что для любого графа сумма степеней всех его вершин

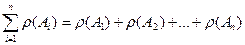(2)

является числом четным, поскольку она равна удвоенному числу ребер.

На графе можно различать два типа вершин: нечетные вершиныА', степени р(А') которых нечетны, и четные вершиныА", имеющие четные степени р(А"). Так, в случае графа рис. 1 вершины А, В, D, Е являются нечетными, а вершины С и F четны. Если вершины расположить в алфавитном порядке, то сумма (2) будет равна

3+3+2+3+3+4=18.

Эта сумма четна, так как число ее нечетных слагаемых равно четырем. Вообще, для того чтобы узнать, будет ли сумма целых чисел четной или нечетной, мы можем не рассматривать четные слагаемые; сумма будет четной или нечетной в зависимости от четности или нечетности числа ее нечетных слагаемых. А так как сумма (2) всегда является четной, мы приходим к следующему результату.

Теорема 1. Число нечетных вершин любого графа четно.

Это утверждение справедливо и в случае, когда граф вовсе не содержит нечетных вершин, так как 0 является числом четным.

Бывают графы, у которых степени всех вершин одинаковы:

р(А₁)=р(А₂)=... =р(А_n)=r.

Такой граф называется однородным графомстепени r; в силу формулы (1) число его ребер равно

N= (1/2) nr

где n – число вершин этого графа. Граф, изображенный на рис. 17 является однородным, его степень равна трем; граф, изображенный на рис. 18 также однородный, и его степень равна четырем.

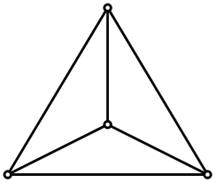
Рис. 17. Однородный граф степени r = 3

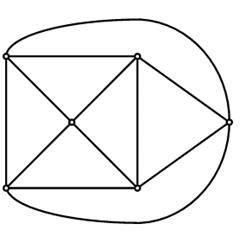
Рис. 18. Однородный граф степени r = 4

В полном графе U_n с n вершинами из каждой вершины выходит n – 1 ребер, ведущих к каждой из остальных n – 1 вершин; таким образом, U_n является однородным графомстепени n – 1. Нуль-граф 0 _n тоже является однородным по той простой причине, что для каждой его вершины р(А)= 0.