С п о с о б ы з а д а н и я б и н а р н ы х о т н о ш е н и й

Известны как минимум четыре разных способа задания отношений (рис. 1.24). Какой из них в каком случае удобнее использовать, зависит от свойств множества X.

1. Непосредственное перечисление всех пар элементов, состоящих в некотором бинарном отношении, возможно только в случае конечного множества X.

2. Матричный способ задания бинарного отношения R на конечном множестве X заключается в нумерации всех элементов множества, так что матрица отношения R будет определяться своими элементами:

Примером подобного способа задания отношений может служить турнирная таблица, в которой проигрыши и ничьи обозначены нулями, а победы – единицами: такая матрица задает отношение вида «x_i – победитель x_j».

3. Задание отношения R с помощью сечений используется для определения отношений на бесконечных множествах. Множество

называется верхним сечением отношения R, а множество

называется нижним сечением отношения R.

Рис. 1.24. Способы задания бинарных отношений

Иначе говоря, верхнее сечение представляет собой множество всех элементов , которые состоят в отношении R с заданным элементом , т.е. 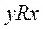. Нижнее сечение – множество всех , с которыми заданный элемент находится в отношении R, т.е.: . Отношениеопределяется однозначно одним из сечений: верхним или нижним.

4. Задание отношения с помощью графа (см. п. 1.6.5). Вершинам графа G(R) соответствуют пронумерованные элементы множества X, а дугам (ребрам) графа соответствует наличие отношения R между теми элементами, которые это ребро соединяет между собой; если же , то ребро (дуга) между x_i и x_j отсутствует (рис. 1.25).

5.

Рис. 1.25. Граф, задающий отношение R между элементами множества X

Рассмотрим некоторые элементарные свойства отношений, которые помогут впоследствии получать модели для решения нужных прикладных задач.

Date: 2016-02-19; view: 500; Нарушение авторских прав