Сосредоточенные и распределенные модели

Математическими моделями на микроуровнепроектирования служат дифференциальные уравнения в частных производных или интегральные уравнения, описывающие поля физических величин, т.е. модели с распределенными параметрами. Независимыми переменными являются пространственные координаты x, y, z и время t. Примерами таких моделей являются уравнения математической физики с заданными краевыми условиями. Например, уравнение теплопроводности:

которое описывает зависимость температуры Т не только от времени t, но и от расстояния x сечения стержня от нагреваемого конца (рис. 1.19).

Рис. 1.19. Изменение температуры в зависимости от времени и расстояния сечения от нагреваемого конца

Уравнения математической физики имеют общий вид: LV(z)=f(z), где z =(t,x,y,z) – вектор независимых переменных; L – дифференциальный оператор; V( z ) – функция, определяемая природой описываемого объекта.

Другие примеры уравнений в частных производных: уравнения диффузии, упругости, электро- и газодинамики.

Уравнение диффузии описывает зависимость концентрации частиц N не только от времени t, но и от положения (x, y, z) точки в теле (в среде):

где D – коэффициент диффузии.

Уравнения непрерывности описывают изменения дырочного и электронного токов в полупроводниковых приборах. Для дырок:

для электронов:

где p – концентрация дырок, n – электронов; q – заряд электрона; J_p и J_n – плотности дырочного и электронного токов; g_p и g_n – скорости процессов генерации-рекомбинации дырок и электронов.

Уравнение теплопроводности в общем случае трех пространственных координат (а не только одной, как в случае со стержнем) также записывается через дивергенцию и градиент температуры:

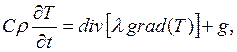
где С – удельная теплоемкость; D – плотность; Т – температура; t – время;

8 – коэффициент теплопроводности; g – количество теплоты, выделяемой в единицу времени в единице объема.

Напомним, что градиент есть векторная функция:

Если обозначить частные производные

то дивергенцию – скалярную функцию – можно записать в следующем виде:

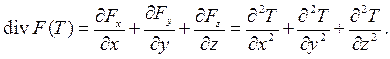
Date: 2016-02-19; view: 478; Нарушение авторских прав