
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача 3. 3а). Степень колеблемости признака определяется по значению коэффициента вариации Vsв соответствии с оценочной шкалой колеблемости признака:
|
|
3а). Степень колеблемости признака определяется по значению коэффициента вариации V s в соответствии с оценочной шкалой колеблемости признака:
0%<V s  40% - колеблемость незначительная;
40% - колеблемость незначительная;
40%< V s  60% - колеблемость средняя (умеренная);
60% - колеблемость средняя (умеренная);
V s >60% - колеблемость значительная.
Вывод:
Для признака Среднегодовая стоимость основных производственных фондов показатель V s =………….. Так как значение показателя лежит в диапазоне ……………………….. оценочной шкалы, следовательно, колеблемость ………………………………..
Для признака Выпуск продукции показатель V s =…………. Так как значение показателя лежит в диапазоне ……………………….. оценочной шкалы, следовательно, колеблемость ………………………………..
3б). Степень однородности совокупности по изучаемому признакудля нормального и близких к нормальному распределений устанавливается по значению коэффициента вариации V s. Если V s 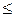 33%, то по данному признаку расхождения между значениями признака невелико. Если при этом единицы наблюдения относятся к одному определенному типу, то изучаемая совокупность однородна.
33%, то по данному признаку расхождения между значениями признака невелико. Если при этом единицы наблюдения относятся к одному определенному типу, то изучаемая совокупность однородна.
Вывод:
Для признака Среднегодовая стоимость основных производственных фондов показатель  , следовательно, по данному признаку выборочная совокупность …………………………..
, следовательно, по данному признаку выборочная совокупность …………………………..
Для признака Выпуск продукции показатель  , следовательно, по данному признаку выборочная совокупность …………………………..
, следовательно, по данному признаку выборочная совокупность …………………………..
3в). Для оценки количества попаданий индивидуальных значений признаков xi в тот или иной диапазон отклонения от средней 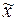 , а также для выявления структуры рассеяния значений xi по 3-м диапазонам формируется табл.9 (с конкретными числовыми значениями границ диапазонов).
, а также для выявления структуры рассеяния значений xi по 3-м диапазонам формируется табл.9 (с конкретными числовыми значениями границ диапазонов).
Таблица 9
Распределение значений признака по диапазонам рассеяния признака относительно 
| Границы диапазонов, млн. руб. | Количество значений xi, находящихся в диапазоне | Процентное соотношение рассеяния значений xi по диапазонам, % | ||||
| Первый признак | Второй признак | Первый признак | Второй признак | Первый признак | Второй признак | |
| А | ||||||

| [………….;………….] | [………….;……….] | ||||

| [………….;………….] | [………….;……….] | ||||
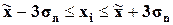
| [………….;………….] | [………….;……….] |
На основе данных табл.9 структура рассеяния значений признака по трем диапазонам (графы 5 и 6) сопоставляется со структурой рассеяния по правилу «трех сигм», справедливому для нормальных и близких к нему распределений:
68,3% значений располагаются в диапазоне ( ),
),
95,4% значений располагаются в диапазоне ( ),
),
99,7% значений располагаются в диапазоне ( ).
).
Если полученная в табл. 9 структура рассеяния хi по 3-м диапазонам незначительно расходится с правилом «трех сигм», можно предположить, что распределение единиц совокупности по данному признаку близко к нормальному.
Расхождение с правилом «трех сигм»может быть существенным. Например, менее 60% значений хi попадают в центральный диапазон ( ) или значительно более 5% значения хi выходит за диапазон (
) или значительно более 5% значения хi выходит за диапазон ( ). В этих случаях распределение нельзя считать близким к нормальному.
). В этих случаях распределение нельзя считать близким к нормальному.
Вывод:
Сравнение данных графы 5 табл.9 с правилом «трех сигм» показывает на их незначительное (существенное) расхождение, следовательно, распределение единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов можно (нельзя) считать близким к нормальному.
Сравнение данных графы 6 табл.9 с правилом «трех сигм» показывает на незначительное (существенное) расхождение, следовательно, распределение единиц совокупности по признаку Выпуск продукции можно (нельзя) считать близким к нормальному.
Задача 4. Для ответа на вопросы 4а) – 4в) необходимо воспользоваться табл.8 и сравнить величины показателей для двух признаков.
Для сравнения степени колеблемости значений изучаемых признаков, степени однородности совокупности по этим признакам, надежности их средних значений используются коэффициенты вариации V s признаков.
Вывод:
Так как V s для первого признака больше (меньше), чем V s для второго признака, то колеблемость значений первого признака больше (меньше) колеблемости значений второго признака, совокупность более однородна по первому (второму) признаку, среднее значение первого признака является более (менее) надежным, чем у второго признака.
Задача 5. Интервальный вариационный ряд распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов представлен в табл.7, а его гистограмма и кумулята – на рис.2.
Возможность отнесения распределения признака «Среднегодовая стоимость основных производственных фондов» к семейству нормальных распределений устанавливается путем анализа формы гистограммы распределения. Анализируются количество вершин в гистограмме, ее асимметричность и выраженность «хвостов», т.е. частоты появления в распределении значений, выходящих за диапазон (  ).
).
1. При анализе формы гистограммы прежде всего следует оценить распределение вариантов признака по интервалам (группам). Если на гистограмме четко прослеживаются два-три «горба» частот вариантов, это говорит о том, что значения признака концентрируются сразу в нескольких интервалах, что не соответствует нормальному закону распределения.
Если гистограмма имеет одновершинную форму, есть основания предполагать, что выборочная совокупность может иметь характер распределения, близкий к нормальному.
2. Для дальнейшего анализа формы распределения используются описательные параметры выборки – показатели центра распределения ( , Mo, Me) и вариации (
, Mo, Me) и вариации ( ). Совокупность этих показателей позволяет дать качественную оценку близости эмпирических данных к нормальной форме распределения.
). Совокупность этих показателей позволяет дать качественную оценку близости эмпирических данных к нормальной форме распределения.
Нормальное распределение является симметричным, и для него выполняются соотношения:
 =Mo=Me
=Mo=Me
Нарушение этих соотношений свидетельствует о наличии асимметрии распределения. Распределения с небольшой или умеренной асимметрией в большинстве случаев относятся к нормальному типу.
3. Для анализа длины «хвостов» распределения используется правило «трех сигм». Согласно этому правилу в нормальном и близким к нему распределениях крайние значения признака (близкие к хmin и хmax) встречаются много реже (5-7 % всех случаев), чем лежащие в диапазоне ( ). Следовательно, по проценту выхода значений признака за пределы диапазона (
). Следовательно, по проценту выхода значений признака за пределы диапазона (  ) можно судить о соответствии длины «хвостов» распределения нормальному закону.
) можно судить о соответствии длины «хвостов» распределения нормальному закону.
Вывод:
1.Гистограмма является одновершинной (многовершинной).
2. Распределение приблизительно симметрично (существенно асимметрично), так как параметры  , Mo, Me отличаются незначительно (значительно):
, Mo, Me отличаются незначительно (значительно):
 =.............., Mo=.............., Me=..............
=.............., Mo=.............., Me=..............
3. “Хвосты” распределения не очень длинны (являются длинными), т.к. согласно графе 5 табл.9…..……% вариантов лежат за пределами интервала ( )=(………………;…………….) млн. руб.
)=(………………;…………….) млн. руб.
Следовательно, на основании п.п. 1,2,3, можно (нельзя) сделать заключение о близости изучаемого распределения к нормальному.
II. Статистический анализ генеральной совокупности
Задача 1. Рассчитанные в табл.3 генеральные показатели представлены в табл.10.
Таблица 10
Описательные статистики генеральной совокупности
| Обобщающие статистические показатели совокупности по изучаемым признакам | Признаки | |
| Среднегодовая стоимость основных производственных фондов | Выпуск продукции | |
Стандартное отклонение  , млн. руб. , млн. руб.
| ||
Дисперсия 
| ||
| Асимметричность As | ||
| Эксцесс Ek |
Для нормального распределения справедливо равенство
RN=6 s N.
В условиях близости распределения единиц генеральной совокупности к нормальному это соотношение используется для прогнозной оценки размаха вариации признака в генеральной совокупности.
Ожидаемый размах вариации признаков RN:
- для первого признака RN =………...............,
- для второго признака RN =………...............
Соотношениемежду генеральной и выборочной дисперсиями:
- для первого признака 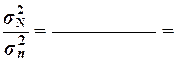 ……, т.е. расхождение между дисперсиями незначительное (значительное);
……, т.е. расхождение между дисперсиями незначительное (значительное);
-д ля второго признака  ……, т.е. расхождение между дисперсиями незначительное (значительное).
……, т.е. расхождение между дисперсиями незначительное (значительное).
Задача 2. Применение выборочного метода наблюдения связано с измерением степени достоверности статистических характеристик генеральной совокупности, полученных по результатам выборочного наблюдения. Достоверность генеральных параметров зависит от репрезентативности выборки, т.е. от того, насколько полно и адекватно представлены в выборке статистические свойства генеральной совокупности.
Как правило, статистические характеристики выборочной и генеральной совокупностей не совпадают, а отклоняются на некоторую величину ε, которую называют ошибкой выборки(ошибкой репрезентативности). Ошибка выборки – это разность между значением показателя, который был получен по выборке, и генеральным значением этого показателя. Например, разность
 = |
= |  -
-  |
|
определяет ошибку репрезентативности для средней величины признака.
Так как ошибки выборки всегда случайны, вычисляют среднюю и предельную ошибки выборки.
1. Для среднего значения признака средняя ошибка выборки  (ее называют также стандартной ошибкой) выражает среднее квадратическое отклонение s выборочной средней
(ее называют также стандартной ошибкой) выражает среднее квадратическое отклонение s выборочной средней  от математического ожидания M[
от математического ожидания M[  ] генеральной средней
] генеральной средней  .
.
Для изучаемых признаков средние ошибки выборки  даны в табл. 3:
даны в табл. 3:
- для признака Среднегодовая стоимость основных производственных фондов
 =……………….,
=……………….,
- для признака Выпуск продукции
 = ………………..
= ………………..
2. Предельная ошибка выборки  определяет границы, в пределах которых лежит генеральная средняя
определяет границы, в пределах которых лежит генеральная средняя  . Эти границы задают так называемый доверительный интервал генеральной средней
. Эти границы задают так называемый доверительный интервал генеральной средней  – случайную область значений, которая с вероятностью P, близкой к 1, гарантированно содержит значение генеральной средней. Эту вероятность называют доверительной вероятностью или уровнем надежности.
– случайную область значений, которая с вероятностью P, близкой к 1, гарантированно содержит значение генеральной средней. Эту вероятность называют доверительной вероятностью или уровнем надежности.
Для уровней надежности P=0,954; P=0,683 оценки предельных ошибок выборки  даны в табл. 3 и табл. 4.
даны в табл. 3 и табл. 4.
Для генеральной средней предельные значения и доверительные интервалы определяются выражениями:
 ,
,

Предельные ошибки выборки и ожидаемые границы для генеральных средних представлены в табл. 11.
Таблица 11
Предельные ошибки выборки и ожидаемые границы для генеральных средних
| Доверительная вероятность Р | Коэффи-циент доверия t | Предельные ошибки выборки, млн. руб. | Ожидаемые границы для средних 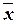 , млн. руб. , млн. руб.
| ||
| для первого признака | для второго признака | для первого признака | для второго признака | ||
| 0,683 | 
| 
| |||
| 0,954 | 
| 
|
Вывод:
Увеличение уровня надежности ведет к расширению (сужению) ожидаемых границ для генеральных средних.
Задача 3. Рассчитанныев табл.3значения коэффициентов асимметрии As и эксцесса Ek даны в табл.10.
1.Показатель асимметрии As оценивает смещение ряда распределения влево или вправо по отношению к оси симметрии нормального распределения.
Если асимметрия правосторонняя (As >0) то правая часть эмпирической кривой оказывается длиннее левой, т.е. имеет место неравенство  > Me>Mo, что означает преимущественное появление в распределении более высоких значений признака (среднее значение
> Me>Mo, что означает преимущественное появление в распределении более высоких значений признака (среднее значение  больше серединного Me и модального Mo).
больше серединного Me и модального Mo).
Если асимметрия левосторонняя (As <0), то левая часть эмпирической кривой оказывается длиннее правой и выполняется неравенство  < Me<Mo, означающее, что в распределении чаще встречаются более низкие значения признака (среднее значение
< Me<Mo, означающее, что в распределении чаще встречаются более низкие значения признака (среднее значение  меньше серединного Me и модального Mo).
меньше серединного Me и модального Mo).
Чем больше величина | As |, тем более асимметрично распределение. Оценочная шкала асимметрии:
| As |  0,25 - асимметрия незначительная;
0,25 - асимметрия незначительная;
0,25<| As |  0,5 - асимметрия заметная (умеренная);
0,5 - асимметрия заметная (умеренная);
| As |>0,5 - асимметрия существенная.
Вывод:
Для признака Среднегодовая стоимость основных производственных фондов наблюдается незначительная (заметная, существенная)левосторонняя (правосторонняя) асимметрия. Следовательно, в распределении преобладают …………………………………………………………………………………………
Для признака Выпуск продукции наблюдается незначительная (заметная, существенная)левосторонняя (правосторонняя) асимметрия. Следовательно, в распределении преобладают ……………………………………………………….
…………………………………………………………………………………………
2.Показатель эксцесса Ek характеризует крутизну кривой распределения - ее заостренность или пологость по сравнению с нормальной кривой.
Как правило, коэффициент эксцесса вычисляется только для симметричных или близких к ним распределений.
Если Ek >0, то вершина кривой распределения располагается выше вершины нормальной кривой, а форма кривой является более островершинной, чем нормальная. Это говорит о скоплении значений признака в центральной зоне ряда распределения, т.е. о преимущественном появлении в данных значений, близких к средней величине.
Если Ek <0, то вершина кривой распределения лежит ниже вершины нормальной кривой, а форма кривой более пологая по сравнению с нормальной. Это означает, что значения признака не концентрируются в центральной части ряда, а рассеяны по всему диапазону от xmax до xmin.
Для нормального распределения Ek =0. Чем больше абсолютная величина | Ek |, тем существеннее распределение отличается от нормального.
При незначительном отклонении Ek от нуля форма кривой эмпирического распределения незначительно отличается от формы нормального распределения.
Вывод:
1. Так как для признака Среднегодовая стоимость основных производственных фондов Ek> 0 ( Ek< 0 ), то кривая распределения является более островершинной (пологовершинной) по сравнению с нормальной кривой. При этом Ek незначительно (значительно) отличается от нуля (Ek =|…........|) Следовательно, по данному признаку форма кривой эмпирического распределения значительно (незначительно) отличается от формы нормального распределения.
2.Так как для признака Выпуск продукции Ek> 0 ( Ek< 0 ), то кривая распределения является более островершинной (пологовершинной) по сравнению с нормальной кривой. При этом Ek незначительно (значительно) отличается от нуля (Ek =|….........|).Следовательно, по данному признаку форма кривой эмпирического распределения значительно (незначительно) отличается от формы нормального распределения.
III. Экономическая интерпретация результатов статистического исследования предприятий [2]
1. Типичны ли образующие выборку предприятия по значениям изучаемых экономических показателей?
Предприятия с резко выделяющимися значениями показателей приведены в табл.2. После их исключения из выборки оставшиеся 30 предприятий являются типичными (нетипичными) по значениям изучаемых экономических показателей.
2. Каковы наиболее характерные для предприятий значения показателей среднегодовой стоимости основных производственных фондов и выпуска продукции?
Ответ на вопрос следует из анализа данных табл.9, где приведен диапазон значений признака (  ), содержащий наиболее характерные для предприятий значения показателей.
), содержащий наиболее характерные для предприятий значения показателей.
Для среднегодовой стоимости основных производственных фондов наиболее характерные значения данного показателя находятся в пределах от...............………млн. руб. до................…….млн. руб. и составляют..........% от численности совокупности.
Для выпуска продукции наиболее характерные значения данного показа-теля находятся в пределах от...............……. млн. руб. до …..................млн. руб. и составляют...........% от численности совокупности.
3. Насколько сильны различия в экономических характеристиках предприятий выборочной совокупности? Можно ли утверждать, что выборка сформирована из предприятий с достаточно близкими значениями по каждому из показателей?
Ответы на вопросы следуют из значения коэффициента вариации (табл.8), характеризующего степень однородности совокупности (см. вывод к задаче 3б). Максимальное расхождение в значениях показателей определяется размахом вариации Rn. (табл.8).
Для среднегодовой стоимости основных производственных фондов различия в значениях показателя значительны (незначительны). Максимальное расхождение в значениях данного показателя........................млн. руб.
Для выпуска продукции различия в значениях показателя значительны (незначительны). Максимальное расхождение в значениях данного показателя........................млн. руб.
4. Какова структура предприятий выборочной совокупности по среднегодовой стоимости основных производственных фондов? Каков удельный вес предприятий с наибольшими, наименьшими и типичными значениями данного показатели? Какие именно это предприятия?
Структура предприятий представлена в табл.7 Рабочего файла.
Предприятия с наиболее типичными значениями показателя входят в интервал от.....................млн. руб. до........................млн. руб. Их удельный вес...........%. Это предприятия №№................................................................................
Предприятия с наибольшими значениями показателя входят в интервал от.....................млн. руб. до.......................млн. руб. Их удельный вес...........%. Это предприятия №№......................................................................................................
Предприятия с наименьшими значениями показателя входят в интервал от.....................млн. руб. до........................млн. руб. Их удельный вес...........%. Это предприятия №№..............................................................................................
5. Носит ли распределение предприятий по группам закономерный характер и какие предприятия (с более высокой или более низкой стоимостью основных фондов) преобладают в совокупности?
Ответ на вопрос следует из вывода к задаче 5 и значения коэффициента асимметрии (табл.8).
Распределение предприятий на группы по среднегодовой стоимости основных производственных фондов носит закономерный характер, близкий к нормальному (незакономерный характер). В совокупности преобладают предприятия с более высокой (низкой) стоимостью основных фондов.
6. Каковы ожидаемые средние величины среднегодовой стоимости основных фондов и выпуска продукции на предприятиях корпорации в целом? Какое максимальное расхождение в значениях каждого показателя можно ожидать?
Ответ на первый вопрос следует из данных табл.11. Максимальное расхождение в значениях показателя определяется величиной размаха вариации RN.
По корпорации в целом ожидаемые с вероятностью 0,954 средние величины показателей находятся в интервалах:
для среднегодовой стоимости основных производственных фондов - от.........................млн. руб. до.........................млн. руб.;
для выпуска продукции - от......................млн. руб. до......................млн. руб.;
Максимальные расхождения в значениях показателей:
для среднегодовой стоимости основных производственных фондов -...................... млн. руб.;
для выпуска продукции -.......................млн. руб.
Date: 2016-02-19; view: 805; Нарушение авторских прав