
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференциальные уравнения с разделяющимися переменными
|
|
Справедливости ради следует заметить, что очень редко ДУ сразу дается в симметрической форме с разделенными переменными. Рассмотрим уравнения, которые можно привести к такому виду.
Пусть ДУ приведено к симметрической форме  . В нем можно разделить переменные, если выражения
. В нем можно разделить переменные, если выражения  и
и  можно представить в виде произведения двух сомножителей, каждое из которых зависит или только от х или только от у, т.е.
можно представить в виде произведения двух сомножителей, каждое из которых зависит или только от х или только от у, т.е.
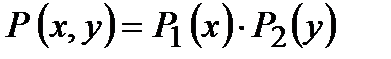 ,
,  .
.
Новый вид уравнения  .
.
Для разделения переменных нужно обе части уравнения поделить (или умножить) на те сомножители, которые «мешают».
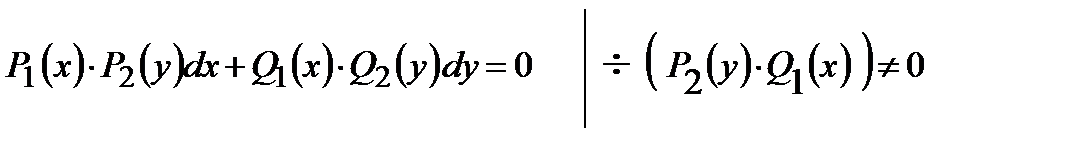

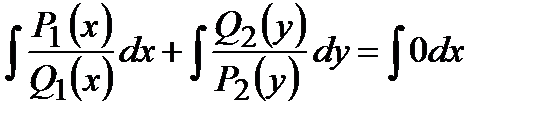
Пример 17. Решить уравнение 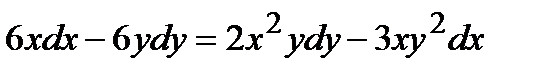
Решение. Сначала преобразуем уравнение так, чтобы символы  и
и 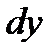 присутствовали по одному разу:
присутствовали по одному разу:
 Þ
Þ  .
.
Теперь представим в виде произведений выражения перед  и
и 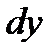 :
:

Разделим переменные:


Проинтегрируем: 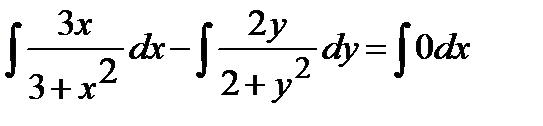 Þ
Þ  Þ
Þ  Þ
Þ
Þ 
Полученное уравнение уже является общим решением дифференциального уравнения или иначе общим интегралом. В принципе можно считать уравнение решенным. Однако, решение очень громоздкое. Его можно упростить. Во всех дальнейших преобразованиях нам понадобится один искусственный прием переобозначения константы С. Как известно, константа С пробегает все значения от  до
до 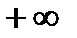 и неважно каким способом. Поэтому зададим нужный нам способ изменения С. В данном конкретном примере выгодно заменить С на
и неважно каким способом. Поэтому зададим нужный нам способ изменения С. В данном конкретном примере выгодно заменить С на  , где
, где  . В дальнейшем замену константы С на другой вид будем обозначать символом
. В дальнейшем замену константы С на другой вид будем обозначать символом  . Для преобразований используем свойства логарифмов.
. Для преобразований используем свойства логарифмов.
 Þ
Þ  Þ
Þ  .
.
Последнее уравнение является более компактной формой общего интеграла. На этом решение дифференциального уравнения можно закончить.
Ответ. Общий интеграл дифференциального уравнения имеет вид
 .
.
Замечание. В примере 2 не сказано конкретно, что нужно найти – общий интеграл или общее решение. Если общий интеграл, то пример 2 решен до конца. Если же подразумевалось общее решение, то тогда из уравнения  нужно выразить у через х явно.
нужно выразить у через х явно.
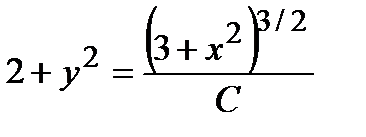 Þ
Þ  .
.
Каждая из полученных функций является общим решением дифференциального уравнения.
Разберем, как решать уравнение с разделяющимися переменными, заданное не в симметрической форме, а в виде  . Первое, что нужно сделать – это перейти к симметрической форме, заменив символ
. Первое, что нужно сделать – это перейти к симметрической форме, заменив символ  на
на
дробь  . Покажем это на конкретном примере.
. Покажем это на конкретном примере.
Пример 18. Найти общий интеграл дифференциального уравнения
 .
.
Решение. Перейдем к симметрической форме, используя равенство  :
:
 Þ
Þ  .
.
Разделим переменные:
 Þ
Þ 
Проинтегрируем полученное уравнение:
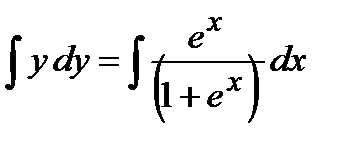 Þ
Þ 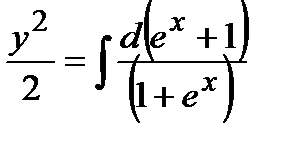 Þ
Þ 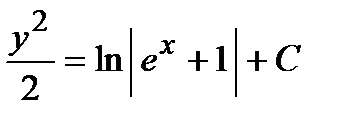 .
.
Последнее уравнение является общим интегралом дифференциального уравнения.
Ответ: Общий интеграл дифференциального уравнения 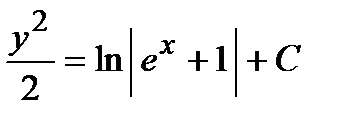 .
.
Date: 2016-02-19; view: 540; Нарушение авторских прав