Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Двумерные непрерывные случайные величины
|
|
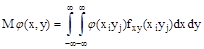
Случайную величину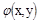 
аппроксимируем дискретной по следующему правилу:
пространство элементарных событий XY представим в виде совокупности прямоугольников с вершинами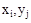 
, если в результате испытания XY попало в прямоугольник (i,j), то эта случайная величина приняла значение 
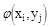. Вероятность наступления этого события равна:
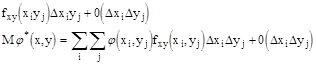
точное значение мат. ожидания
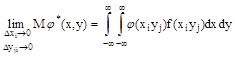
n -мерный дискретный случай
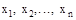- многомерная дискретная случайная величина
Найдем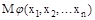 
Вероятностное пространство зададим в виде
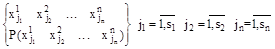
Тогда
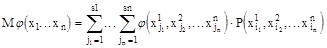
n -мерный непрерывный случай
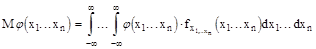
Теорема 1. Математическое ожидание суммы случайных величин равно сумме математических ожиданий
а) дискретный случай
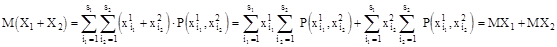
б) непрерывный случай
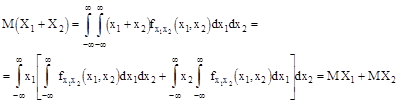
Пусть n-произвольное число
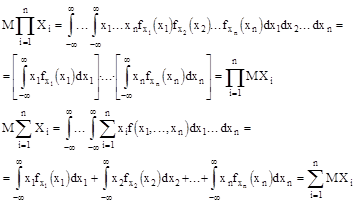
Теорема 2. Математическое ожидание произведения независимых случайных величин равно произведению мат.ожиданий.
По определению имеем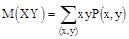 
т.к. случайные величины X и Y независимы, то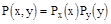 
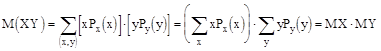
Date: 2015-06-05; view: 486; Нарушение авторских прав