Случайная величина

Пусть имеется вероятностное пространство вида .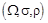

Случайной величиной называется измеримая числовая скалярная функция 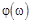, элементами которой являются элементарные события.

Числовая скалярная функция - это функция, удовлетворяющая следующему условию:

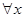событие 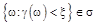- алгебре и, следовательно, имеет вероятность наступления.

Если произведено испытание, в результате которого произошло некоторое элементарное событие 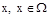. В соответствии с функцией 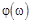этому элементарному событию соответствует число, которое называется реализацией случайной величины x в данном испытании.

В соответствии с определением случайной величины вводится числовая скалярная функция F(x), 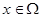, определенная для каждого действительного x и по определению равная вероятности наступления события:

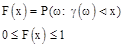
Эта функция называется функцией распределения случайной величины .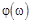

Рассмотрим три события:

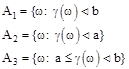
где a<b, a, b - действительные числа.

Свойства:

Покажем, что из факта

A₂ Ì s-алгебре

A₁ Ì s-алгебре

и равенства 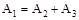следует, что A₃ Ì s.

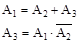
По определению s-алгебры A₃ измерима, поэтому можно принять III аксиому теории вероятности:

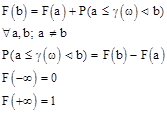
F(x) - неубывающая функция

Если x<y, то

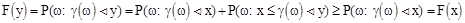
т.к. 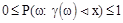, то преобразования верны.

Для всех технических приложений функцию распределения можно считать направленной слева.

В силу того, что функция распределения не убывает, она однозначно задает стчетно-аддитивную меру на поле, порожденном всеми полуинтервалами ненулевой длины.

По введенному полю построим борелевскую алгебру. Обозначим ее b. Возьмем произвольное число BÌb не принадлежащее полю. Это точка или сегмент. Т.к. множество 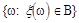получено с помощью счетной суммы или счетного пересечения множеств принадлежащих s-алгебре, то и это множество принадлежит s-алгебре и, следовательно, существует вероятность наступления события B. Следовательно, имеет место следующее эквивалентное определение измеримой функции.

Функция 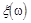называется измеримой, если для любого BОb множество

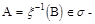алгебре

где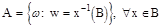

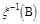множество, полученное следующим образом:

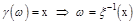
Функция g(x) называется борелевской функцией, если для любого BÌb множество

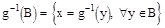
Борелевская функция - функция, определяемая на системе борелевских множеств.

В функциональном анализе показано, что все известные аналитические функции являются борелевскими.

ТЕОРЕМА:

Пусть g(x) борелевская функция, 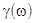- случайная величина, т.е. измеримая функция. Тогда функция

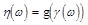
является измеримой и, следовательно, случайной величиной.

Берем произвольное BÌb. 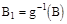по определению борелевской функции.

Рассмотрим множество

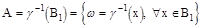
т.к. 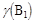измеримая функция и 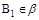, то AÌs-алгебре

Следовательно, функция 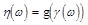- измеримая функция, т.е. случайная величина.

Date: 2015-06-05; view: 470; Нарушение авторских прав