Теорема синусов. В любом сферическом треугольнике отношения синусов сторон равны отношениям синусов противолежащих им углов

В любом сферическом треугольнике отношения синусов сторон равны отношениям синусов противолежащих им углов.

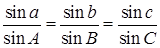. (1.1)

Далее следуют теоремы для четырех элементов сферического треугольника.

Теорема косинусов сторон (три стороны и один угол)

Косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов этих же сторон на косинус угла между ними.

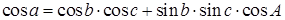
(1.2)

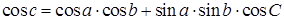
Теорема косинусов углов (три угла и одна сторона)

Во всяком сферическом треугольнике косинус угла равен произведению косинусов двух других углов, взятому с обратным знаком, плюс произведение синусов этих углов, умноженное на косинус стороны между ними.

Другими словами, здесь используются формулы (1.2), только вместо сторон записываются углы и наоборот, и перед произведением косинусов ставится знак минус.

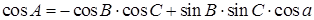
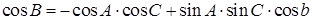(1.3)

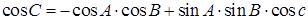
Теорема котангенсов (две стороны и два угла)

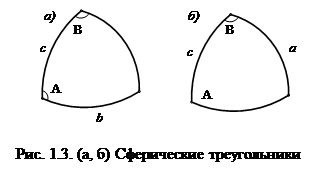
Прежде чем дать формулировку теоремы выделим из четырех элементов сферического треугольника крайние и средние элементов.

Например, на рис. 1.3, а элементы b, B – крайние, а элементы A, c – средние. На рис. 1.3, б элементы a, A – крайние, а B, c – средние.

А теперь сформулируем теорему:

Котангенс крайнего угла на синус среднего угла равен произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов [5].

Для рис. 1.3, а: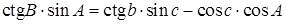

(1.4)

Для рис. 1.3, б: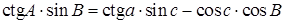

Формулы пяти элементов (три стороны, два угла)

а) во всяком сферическом треугольнике произведение синуса стороны на косинус прилегающего к ней угла равно произведению косинуса на синус двух других сторон, минус произведение синуса и косинуса этих же сторон, умноженное на косинус угла между ними.

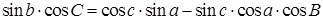(1.5)

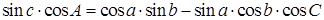
б) (три угла, две стороны). Здесь используются формулы (1.5), только вместо сторон записываются углы и, наоборот, и вместо знака минус перед вторым произведением ставится знак плюс.

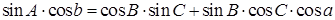
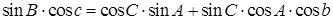(1.6)

.

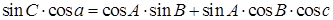Date: 2015-06-05; view: 1169; Нарушение авторских прав