Выполнить устных упражнений по готовым рисункам

Задание. Докажите для каждого из случаев (рис. 12, а — г), что

четырехугольник ABCD — параллелограмм.

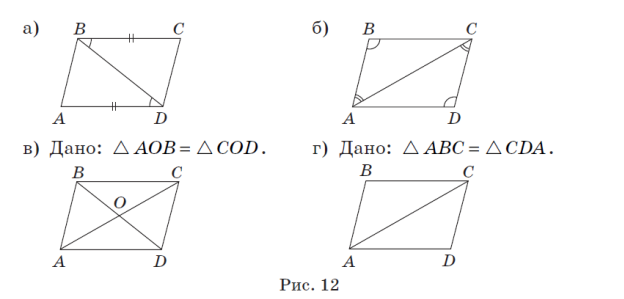
Доказательство

По данным рис. 12, а, ∠ CBD =∠ ADB. Поскольку эти углы —внутренние накрест лежащие при прямых BC и AD и секущей BD, то BC ǁ AD. Так как по условию BC = AD, то четырехугольник ABCD —параллелограмм по признаку.

По данным рис. 12, б, ∠ B =∠ D, ∠ BAC =∠ DCA. Так как сумма углов любого треугольника равна 180°, то из равенства углов следует, что ∠ BCA =∠ DAC, а значит, и ∠ BCD =∠ BAD. Таким образом, у четырехугольника ABCD противолежащие углы попарно равны. Следовательно, четырехугольник ABCD — параллелограмм по признаку.

Из равенства треугольников AOB и COD (рис. 12, в) следует, что BO = OD, AO = OC. Значит, диагонали четырехугольника ABCD делятся точкой пересечения пополам. Следовательно, четырехугольник ABCD — параллелограмм по признаку.

Из равенства треугольников ABC и CDA (рис. 12, г) следует, что AB = CD и BC = AD. Значит, противолежащие стороны попарно равны. Следовательно, четырехугольник ABCD — параллелограмм.

Выполнить письменное упражнение

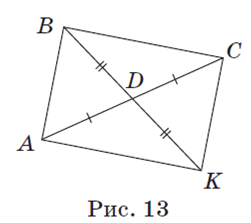
Задача. В треугольнике ABC (рис. 13) на продолжении медианы BD отложен отрезок DK, равный BD. Докажите, что ABCK —параллелограмм.

Доказательство

Поскольку BD — медиана треугольника ABC, значит, AD = DC. BD = DK по условию, таким образом, в четырехугольнике ABCK диагонали делятся точкой пересечения пополам. Следовательно, ABCK — параллелограмм

по признаку, что и требовалось доказать

Домашнее задание

Выучить определения, свойства и признаки, уметь доказывать

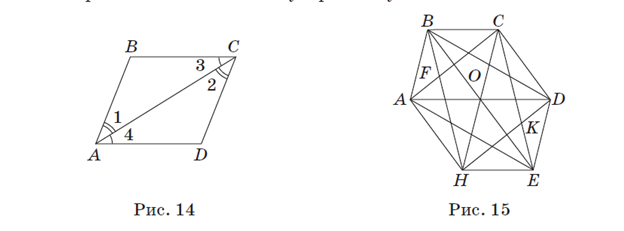
С 1. Дано: ∠1 =∠2; ∠3 =∠4 (рис. 14).

Доказать: ABCD — параллелограмм.

Д 2. На рис. 15 точка O — общая середина отрезков AD, CH, BE.

Какие из четырехугольников на этом рисунке являются параллелограммами и по какому признаку?

Date: 2015-04-23; view: 577; Нарушение авторских прав