Ответить на вопрос

А класс Геометрия

07.10.2014

Тема урока:

Параллелограмм

Записать в тетради число, тему урока

Актуализация опорных знаний

Выполнить задания

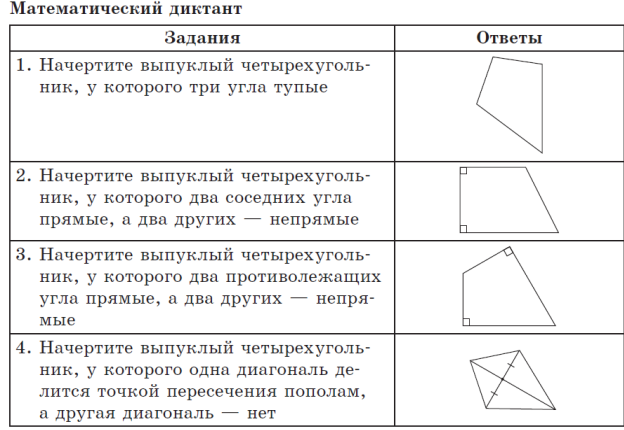
1. Укажите пары внутренних накрест лежащих углов и пары внутренних односторонних углов на рис. 3. Являются ли прямые c и d параллельными, если: а) ∠1 =∠4; б) ∠1 = 60°, ∠3 =120°?

2. На рис. 4 ∠ A = 30°, ∠ B =150°. Докажите что BC  AD.

3. AC — диагональ четырехугольника ABCD (рис. 5). Докажите, что BC ǁ AD и AB ǁ CD, если Δ ABC =Δ CDA.

4. Какова особенность четырехугольника, полученного при решении

задания 5 математического диктанта?

Изучение нового материала

План изучения темы

1. Определение параллелограмма.

2. Признаки параллелограмма.

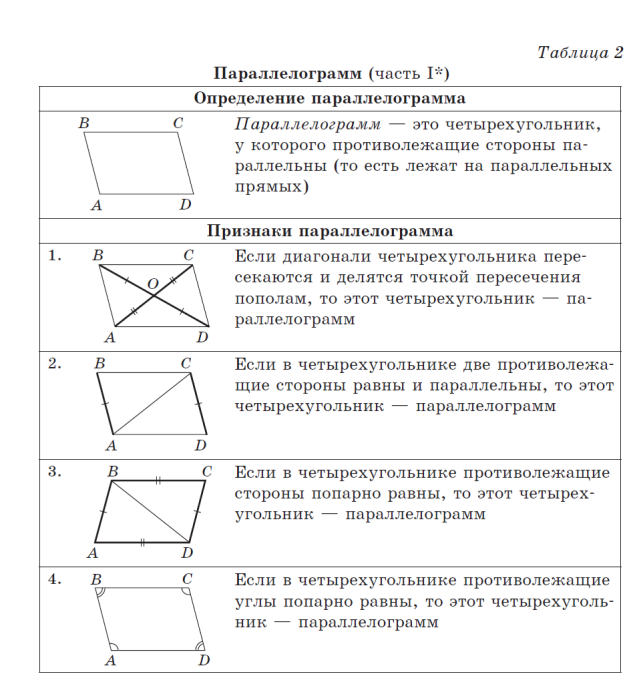
Ответить на вопрос

• Какие ошибки допущены в изображении параллелограммов на рис. 6 и 7?

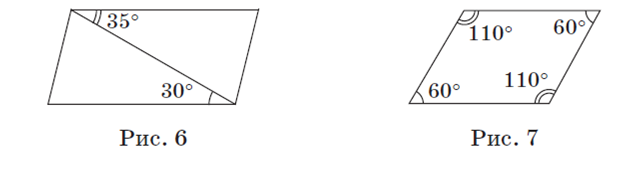
Признаки параллелограмма

Задача 1 (признак 1). Е сли диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник— параллелограмм.

Доказательство

Пусть ABCD — данный четырехугольник, диагонали которого

пересекаются в точке O (рис. 8). В треугольниках BOC и DOA:

BO = DO, OC = OA — по условию; ∠ BOC =∠ DOA как вертикальные.

Значит, Δ BOC =Δ DOA по двум сторонам и углу между ними. От-

сюда ∠ BCO =∠ DAO, причем эти углы внутренние накрест лежащие

при прямых BC и AD и секущей AC. Следовательно, BC ǁ AD. Аналогично доказываем равенство треугольников BOA и DOC и параллельность прямых AB и CD. Так как противолежащие стороны четырехугольника параллельны, то этот четырехугольник — параллелограмм по определению, что и требовалось доказать.

Задача 2 (признак 2). Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник —

параллелограмм.

Доказательство

Пусть в четырехугольнике ABCD (рис. 9) AB ǁ CD, AB = CD. В дан-

ном четырехугольнике проведем диагональ AC. Так как AB  CD, а AC — секущая, то ∠ BAC =∠ DCA как внутренние накрест лежащие при параллельных прямых и секущей. AC — общая сторона треугольников BAC и DCA, AB  CD по условию. Значит, Δ BAC =Δ DCA по двум сторонам и углу между ними. Отсюда ∠ BCA ∠ DAC. Поскольку эти углы внутренние накрест лежащие при прямых BC

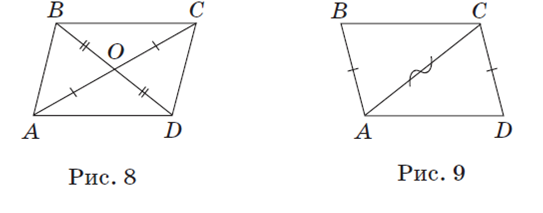
и AD и секущей AC, то BC ǁ AD. Следовательно, AB ǁ CD, BC ǁ AD.

Таким образом, в четырехугольнике ABCD противолежащие стороны

параллельны, следовательно, он параллелограмм по определению,

что и требовалось доказать.

Задача 3 (признак 3). Если в четырехугольнике противолежащие

стороны попарно равны, то этот четырехугольник — параллелограмм.

Доказательство

Пусть в четырехугольнике ABCD (рис. 10) AB = CD, BC = AD.

В данном четырехугольнике проведем диагональ AC. В треугольниках

ABC и CDA: AB = CD, BC = AD — по условию, AC — общая сторона.

Значит, Δ ABC =Δ CDA по трем сторонам. Отсюда ∠ BAC =∠ DCA,

∠ BCA =∠ DAC как соответствующие углы равных треугольников. Поскольку углы BAC и DCA — внутренние накрест лежащие при прямых AB и CD и секущей AC, а углы BCA и DAC — внутренние накрест лежащие при прямых BC и AD и секущей AC, то соответственно AB  CD, BC  AD. Следовательно, четырехугольник ABCD —параллелограмм по определению, что и требовалось доказать.

Задача 4 (признак 4). Если у четырехугольника противолежащие углы попарно равны, то этот четырехугольник — параллелограмм.

Доказательство

Как уже было доказано, сумма углов любого четырехугольника

равна 360º. Пусть в четырехугольнике ABCD (рис. 11) ∠ A+ ∠ C,

∠ B =∠ D. Так как ∠ A +∠ B +∠ C +∠ D =360º, то 2(∠ A +∠ B) =360º.

Отсюда ∠ A +∠ B =180º. Поскольку углы A и B — внутренние односторонние при прямых BC и AD и секущей AB, то BC  AD по признаку параллельности прямых. Аналогично ∠ A +∠ D =180º, а значит, AB ǁ CD. Следовательно, четырехугольник ABCD — параллелограмм по определению, что и требовалось доказать.

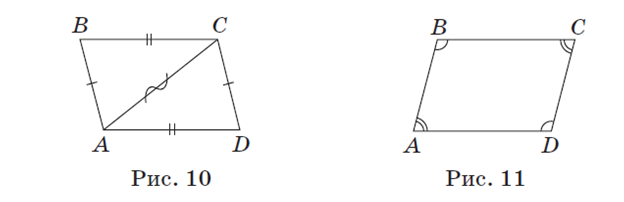
Закрепление новых знаний

Date: 2015-04-23; view: 958; Нарушение авторских прав