Выполнение письменных упражнений. Задача 1.В четырехугольнике ABCD (рис

Задача 1. В четырехугольнике ABCD (рис. 3) AB = BC, ∠ CBD = ∠ ABD

∠ CBD = ∠ ABD. Докажите, что CD = AD. Как называется такой четы-

рехугольник?

Решение

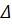ABD = Δ CBD по двум сторонам и углу между ними (AB = BC

и ∠ ABD =∠ CBD по условию, BD — общая сторона). Тогда AD = CD

как соответствующие стороны равных треугольников. Следовательно,

ABCD — дельтоид.

З адача 2. Докажите, что сумма углов любого четырехугольника

равна 360°.

Доказательство

Рассмотрим четырехугольник ABCD (рис. 4): AC — диагональ

четырехугольника, которая разбивает его на два треугольника ABC

и ADC.

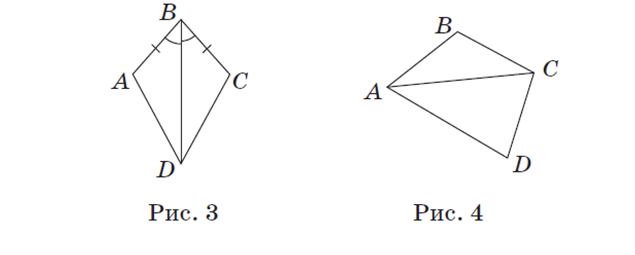
В треугольнике ABC: ∠ ABC +∠ BAC +∠ BCA =180°. В треуголь-

нике ADC: ∠ ADC +∠ CAD +∠ ACD =180°. Так как луч AC проходит

между сторонами угла BAD, а луч CA проходит между сторонами

угла BCD, то ∠ BAC +∠ CAD =∠ BAD, а ∠ BCA +∠ ACD =∠ BCD. Та-

ким образом, ∠ ABC +∠ BCD +∠ ADC +∠ BAD =180°+180° = 360°, что

и требовалось доказать.

Подведение итогов

• Каким четырем условиям удовлетворяет геометрическая фигура,

если она является четырехугольником? (Геометрическая фигура

состоит из четырех точек и четырех отрезков; никакие три из

этих точек не лежат на одной прямой; отрезки последовательно

соединяют данные точки; эти отрезки не пересекаются.)

Date: 2015-04-23; view: 568; Нарушение авторских прав