
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Принцип дополнительности фрактальной геометрии
|
|
Кроме исследования математических фракталов, Мандельброт предъявил процедуры отождествления математических фракталов и реальных природных и социальных объектов – облаков, рек, береговых линий, капилляров, колебаний цен на рынке.
В статье «Метафизика фрактала»[9] мною было показано то, как введение фрактальной концепции в практику научных исследований разрушает евклидианскую исследовательскую научную программу. Этот процесс был рассмотрен с помощью представлений И. Лакатоса о влиятельной метафизике научной теории (то есть, о положениях, стоящих над эмпирической проверкой и направляющих научный поиск).
Концепция фрактала игнорирует "защитный пояс" классических геометрических концепций (конкретные исчисления, связанные с евклидианской программой фрактальной концепцией даже не критикуются), заменяя "жесткое ядро" - тривиальные первые принципы - категории геометрии. Этим самым задается метафизика фрактала - влиятельная метафизика фрактальной концепции.
Эта замена идет не по пути изменения или введения новой аксиоматики, основанной на строгих логических приемах определения понятия, а по пути введения интерсубъективного контекста фрактальной концепции - создания устойчивых практик узнавания фрактала как в феноменах математики (геометрических множествах, решениях нелинейных уравнений), так и в феноменах - конструктах прикладных теорий (географии, лингвистики, астрофизики).
В связи с этим, можно предложить схему контекстуального введения категории фрактала и задания на этой базе влиятельной метафизики - как самоорганизации коммуникаций, интерсубъективной среды для диалога между учеными, способствующему усилению познавательной ценности категории фрактала.
Мандельброт вводил представления о фрактале фрактально – не жестко и хаотически:
во-первых, Мандельброт ввел термин "фрактал";
во-вторых, он ввел "затравку" - первое - (математически точное, но в общем случае, неверное) определение понятия фрактала через размерность Хаусдорфа-Безиковича;
и, в-третьих, он запустил интерсубъективный механизм "самоорганизации научного понятия" – развил ассоциации между термином "фрактал" и предметами математики и природы в научном сообществе.
Для создания механизма «самоорганизации понятия» Мандельброт сумел описать (пользуясь методами аналогии, компьютерной визуализации, перечислением сходных, по его представлениям, предметных областей, применяя метафоры) способы отождествления (узнавания) различных математических и природных форм как фрактальных, с помощью которых можно было бы расширить "затравочное" определение и произвести диверсификацию понятия фрактала на различные области знания. Тем самым он придал новому понятию категориальный статус и создал на этой базе массовую научную коммуникацию - стратегию диалога, среду самоорганизации нового понятия.
Геометрические объекты, вовлекаемые Мандельбротом в корпус представлений фрактальной концепции давно исследовались математиками, и даже применялись физиками и инженерами, но общего позитивного понятия не было. Не было общей методологии, связывающей в целое представление такие, казалось бы, совершенно не корреспондирующие между собой вещи как, например, множество Жюлиа, колебания цен на хлопок и чертеж побережья Британии.
С методологический точки зрения представляется важным тот факт, что для введения нового понятия - понятия фрактала, Мандельброт не "изобретал" каких-то абсолютно новых формализмов или теорий. Он, скорее, не "первооткрыватель", а "перворассматриватель" - первый-по-новому-рассмотритель - его работа заключалась в перестройке перцептивных схем и создании языка объяснения новых предметов.
Его действия можно интерпретировать как переключение "гештальта" (парадигмы - воспринимающих и интерпретирующих способностей научного сообщества) на сборку нового понятия, на распознавание и интерпретацию фрактальных структур в конкретных познавательных контекстах. Мандельброт создал новые устойчивые перцептивные механизмы, и устойчивые лингвистические коммуникативные практики в науке, призвав научное сообщество по-новому оценить давно известные вещи (например - различные типы размерностей, парадоксы измерения, множества, типа множества Кантора).
Поэтому, фрактальная геометрия не есть "чистая" геометрическая теория. Это скорее концепция, новый взгляд на хорошо известные вещи, перестройка восприятия, заставляющая исследователя по-новому видеть мир.
Мандельброт сделал сильный методологический ход, перейдя от некомуникабельного современной ему науке "чистого" конструктивного "монстра", к фракталу - предмету измерения математики и прикладных наук. Для этого он сконструировал две процедуры отождествления - процедуру отождествления рекурсивных математических "монстров" как фракталов и процедуру отождествления предметов измерения фрактальной концепции и предметов измерения теоретических конструктов прикладных исследований (географии, лингвистики, материаловедения и др.). В этом смысле, он ввел цельность представления в разрозненные нагромождения фактов и моделей, создав (предустановив), по меткой метафоре Ю.А. Данилова, "фрактальную" гармонию - фрактальный порядок интерпретируемого мира. Мандельброт запустил интерсубъективный механизм самодостраивания, самоорганизации этого порядка.
После подобного "переключения внимания" в научном сообществе интерсубъективно фиксируется познавательная ценность категории фрактала, формируется некоторое "личностное" знание - подразумеваемое знание о фрактале, предающее статус очевидности категории фрактала, создающее контекст фрактальной концепции и снимающее необходимость точного определения фрактала.
В диссертационной работе[10] было показано, что введение фрактальной геометрии в практики интерпретации природы можно интерпретировать с точки зрения принципов дополнительности, наблюдаемости и соответствия квантовой механики.
В качестве иллюстрации дополнительности схем измерения фрактальной геометрии, эксплицируем логические процедуры измерения природного фрактала – береговой линии.
С трудностями при измерении длины береговой линии Британии столкнулся в начале нашего века английский гидромеханик Ридчардсон при попытке заменить береговую линию ломаной с длиной L=Nd при исследовании зависимости длины ломаной от шага циркуля в разномасштабных картах (рис. 1.5.1).
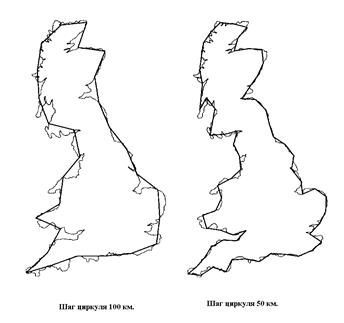 Рис 1.5.1 К измерению длины береговой линии Британии
Рис 1.5.1 К измерению длины береговой линии Британии
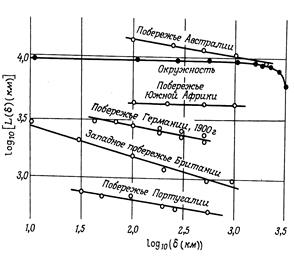 Рис 1.5.2 Зависимость длины побережий L(d) от шага циркуля d.
Оказалось, что при уменьшении единицы измерения d, длина L резко возрастает:
Рис 1.5.2 Зависимость длины побережий L(d) от шага циркуля d.
Оказалось, что при уменьшении единицы измерения d, длина L резко возрастает:
|
Таблица 1.5.1
| Шаг циркуля d, км | Длина L(d), км |
Мандельброт предложил аппроксимировать степень “убегания” длины береговой линии L(d) в зависимости от d степенным законом:
L(d)= a d1-D
Он показал, что размерности D различных побережий отличаются (рис. 1.5.2), и могут служить достаточно информативной географической характеристикой, описывая степень извилистости, скрученности побережья.
Зададимся вопросом - почему факт "разбегания" длины был долгое время – до работ Мандельброта, не замечаем научным сообществом географов? Почему географы не обращали внимания на работы Ридчардсона? Как можно интерпретировать эту селективную избирательность?
Если побережье - "действительно" фрактал, то почему, этого так долго "не замечали" географы? С чем это связано?
С одной стороны, можно сказать, что факт невнимания к аномальному поведению длины побережья - ошибка географов, которую исправила фрактальная теория.
Но как назвать ошибку, для которой не было корректно сформулированной задачи – не существовало образцов ответов?
Поэтому, нам интереснее рассмотреть факт невнимания к результатам Ридчардсона не в терминах ошибки или заблуждения, а в терминах интерсубъективности восприятия предмета исследования.
С этой точки зрения весьма интересной представляется концепция личностного знания М.Полани. Факт невнимания географов к масштабному "разбеганию" длины побережья, выразившийся, в частности, в попытках найти и обосновать "истинный", "самый верный" масштаб измерения обусловлен отсутствием "влиятельной метафизики" и соответствующей ей научной теории, и как следствие - языка описания, способов интерпретации.
В результате этого рождается селективный отбор эмпирических фактов:
"...в научном исследовании всегда имеются какие-то детали, который ученый не удостаивает особым вниманием в процессе верификации точной теории. Такого рода личностная избирательность является неотъемлемой чертой науки." [11]
Когда внимание учного направлено на линию, происходит интенциональный акт понятийного "схватывания" линии, который, несомненно, связан с "влиятельной метафизикой" евклидианской исследовательской программы, определяющей свойства сознания ученого, характеристики познавательной среды, в которую он погружен. Личностная избирательность - результат этого "схватывания", абстрагирования понятия.
Математические «монстры» (затем преобразившиеся в фракталы) - яркий пример личностной избирательности научного сообщества, не желающего принимать "в свою компанию" то, что "противоречит здравому смыслу".
Ситуация становится более интересной, когда появляются дополнительные схемы объяснения, когда бывшие «монстры» теряют свои маргинальные статусы. В дополнительности кроится конфликт, вызов коммуникационной тотальности единой схемы объяснения
Для корректного рассмотрения данной проблемы введем понятие о принципе дополнительности фрактальной геометрии, когда природный феномен, в зависимости от понятийных установок исследователя или научного сообщества, может менять свой понятийный статус.
По аналогии с интерпретацией квантово-механических событий копенгагенской школой Бора и Гейзенберга, можно предположить, что при соотнесении природного феномена с предметами разных теорий (фрактальной геометрией и геометрией Евклида) образуются комплиментарные предложения, по крайней мере одно из которых может быть определенным, тогда как другое - неопределено.
Будем считать, что утверждение о том, является ли природный феномен, например, евклидовой линией или фракталом, является неопределенным до тех пор, пока мы не уточним, в рамках какой теории мы его пытаемся объяснить - на языке фракталов, или на языках других геометрий. Только после такого уточнения и задания соответствующей процедуры отождествления одно из дополнительных понятий приобретает определенность.
Пусть:
А - высказывание “длина побережья Британии равна 2 километра”,
В - высказывание “фрактальная размерность побережья Британии равна 1.23”.
Высказывания А и В находятся в отношении, напоминающим отношение дополнительности в квантовой механике. Если измерена длина побережья, и результаты измерения выражены высказыванием А, то А - истинно или ложно. В этом случае высказывание В о том, что побережье Британии имеет фрактальную размерность принципиально неопределено - фиксированием длины мы задали линейность предмета измерения побережья предустановив ему единичную, нефрактальную размерность.
Длину и фрактальную размерность измерить при одном и том же масштабном преобразовании нельзя. А дополнительно к В. И наоборот - В дополнительно к А. как и в квантовой механике, дополнительность в данном случае симметрична.
Эти высказывания подпадают под определение отношения дополнительности В.С.Меськова[12]: “Два высказывания находятся в отношении дополнительности, если и только если: 1) они не могут быть одновременно истинными; 2) они не могут быть одновременно ложными; 3) если одно из них является истинными или ложным, то второе - неопределенным; 4) если одно из них является неопределенным, то второе может принимать любое из допустимых истинностных значений”.
Данные утверждения могут быть записаны в “трехзначной” логике Рейхенбаха:
АÚ~А®~~ВÛВÚ~В®~~А,
где: Ú - обычная дизъюнкция, ® - альтернативная (по Рейхенбаху) импликация, ~ - “циклическое” (по Рейхенбаху) отрицание.
Как известно, Г. Рейхенбах, наряду с М. Штраусом и П. Феврие был основоположником семантического подхода в логике квантовой механики, суть которого заключалась в логической экспликации дополнительности рассмотрению дополнительности как отношению между высказваниями о дополнительных величинах.

Рис. 1.5.3 Ганс Рейхенбах (1891 - 1953)
Немецкий философ и логик. Профессор философии физики в Берлинском университете. Преподавал в Стамбульском университете и в Калифорнийском университете США.
Рейхенбах приводит следующую таблицу значений[13]:
Таблица 1.5.2
| А | ¾ А | ~А |
| И Н Л | Н И И | Н Л И |
Таблица 1.5.3
| А | В | А\/ В | А ® В |
| И | И | И | И |
| И | Н | И | Л |
| И | Л | И | Л |
| Н | И | И | И |
| Н | Н | Н | И |
| Н | Л | Л | И |
| Л | И | И | И |
| Л | Н | Н | И |
| Л | Л | Л | И |
Введение в предмет рассмотрения фрактальных размерностей или характеристик, связанных с гладкими моделями, зависит от наблюдателя – специфического познавательного субъекта с "загруженными" теоретическими и социокультурными установками.
Изучение когнитивного статуса наблюдателя – любимая тема исследований автопоэзиса. В этом можно найти еще одно концептуальное пересечение теории автопоэзиса и фрактальной геометрии.
Наиболее ярко зависимость от наблюдателя видна на примере введения понятия размерности. Вот, что пишут по этому поводу в уже упоминавшейся статье Ю.А.Данилов и Б.Б.Кадомцев:
“Мандельброт обратил внимание на то, что довольно широко распространенное мнение о том, будто размерность является внутренней характеристикой тела, поверхности или кривой неверно (в действительности, размерность объекта зависит от наблюдателя, точнее от связи объекта с внешним миром).
Суть дела нетрудно уяснить из следующего наглядного примера. Представим себе, что мы рассматриваем клубок ниток. Если расстояние, отделяющее нас от клубка, достаточно велико, то клубок мы видим как точку, лишенную какой бы то ни было внутренней структуры, т. е. геометрический объект с евклидовой (интуитивно воспринимаемой) размерностью 0. Приблизив клубок на некоторое расстояние, мы будем видеть его как плоский диск, т. е. как геометрический объект размерности 2. Приблизившись к клубку еще на несколько шагов, мы увидим его в виде шарика, но не сможем различить отдельные нити - клубок станет геометрическим объектом размерности 3. При дальнейшем приближении к клубку мы увидим, что он состоит из нитей, т. е. евклидова размерность клубка станет равной 1. Наконец, если бы разрешающая способность наших глаз позволяла нам различать отдельные атомы, то, проникнув внутрь нити, мы увидели бы отдельные точки - клубок рассыпался бы на атомы, стал геометрическим объектом размерности 0.”
Возьмем на заметку тот факт, что говоря о зависимости размерности от наблюдателя, авторы подчеркивают прагматику введения размерности, которая носит комплиментарный характер:
“Но если размерность зависит от конкретных условий, то ее можно выбирать по-разному. Математики накопили довольно большой запас различных определений размерности. Наиболее рациональный выбор определения размерности зависит от того, для чего мы хотим использовать это определение. (Ситуация с выбором размерности вполне аналогична ситуации с вопросом: «Сколько пальцев у меня на руках: 3 + 7 или 2 + 8?» До тех пор, пока мы не вздумали надеть перчатки, любой ответ можно считать одинаково правильным. Но стоит лишь натянуть перчатки, как ответ на вопрос становится однозначным: «5 + 5».)
Подчеркнем, что размерность сильно зависит от того как ее измерять. Это означает, что кроме формул для подсчета размерности необходимо точно задать и некий операциональный набор способа измерения размерности.
В одном из первых в отечественной литературе обзоров по фракталам[14] (или фракталям - если сохранять род слова Fractal при переводе), Я.Б. Зельдович и Д.Д. Соколов приводят такой пример. Положение точки области плоскости, ограниченной квадратом можно задать двумя измерениями, и тогда ее размерность будет равна двум, а можно исхитриться, и представить себе эту область в виде ломаной с очень сильно прижатыми друг к другу звеньями, сложенными наподобие столярного метра. Тогда, для задания положения точки хватит и одного измерения, и размерность будет равна единице.
"Монстр" - кривая Пеано (1.3.10) напоминает подобный столярный метр – при уменьшении длины ее звеньев, она начинает заполнять всю плоскость.
Точно таким же свойством обладает траектория броуновской частицы – чем больше время наблюдения, тем плотнее частица заполняет плоскость. Размерность определяет степень сложности траектории частицы в фазовом пространстве, степень негладкости этой траектории.
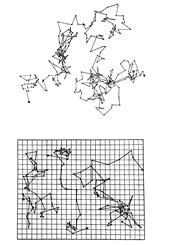
Рис. 1.5.4 Фрактальная траектория броуновской частицы. Рисунок из книги: Mandelbrot B. The Fractal Geometry of Nature. Freeman, San-Francisco.1977
Именно изломанность, пилообразность, негладкость "монстров" вызвала ассоциации при создании термина "фрактал" у Мандельброта[15]:
“В латинском языке есть поговорка: “назвать (именовать) значит узнать”: Nomen est numen. До тех пор, пока я не принялся за своё изучение, упоминаемые в предыдущих разделах множества не нуждались в убедительном термине для их обозначения. Однако, когда классические монстры начали включаться в мои труды, и начали возникать многочисленные новые “монстры”, потребность в термине стала чрезвычайно необходимой. Это стало особенно острым, когда нужно было дать имя первому предшественнику этого эссе."
Термин "фрактал" закрепил и развил новый познавательный статус "монстров". С появлением имени у "монстров" появилось лицо, они перешли из области негативных примеров в область позитивных определений.
1.6 Парадоксы как фракталы. Фрактальная логика: обратная связь как модель "монстров" и парадоксов.
Мандельброт проанализировал "монстров" с точки зрения представлений фрактальной геометрии, показав общность между монстрами, природными объектами и множествами Жюлиа и Мандельброта.
Так же как и эти объекты, "монстры" обладают фрактальной размерностью и демонстрируют самоподобие.
Наиболее ярко понятие самоподобия иллюстрируется с помощью рассмотренной нами ранее фигуры Коха. Действительно, при увеличении ее фрагмента с помощью геометрического преобразования подобия можно получить фигуру тождественную той, чей фрагмент мы увеличивали.
Так же, как и для береговой линии, для кривой Коха или треугольника Серпинского можно вводить разного рода размерности.
В частности, “степень убегания” (1-D) длины (L) фигуры Коха в зависимости от единичной длины звена (d) оценивается по следующей формуле:
L (d) µ d1-D,
где D = ln4/ln3» 1.2628... - предложенная Мандельбротом степенная характеристика “убегания длины” или фрактальная размерность (по определению) триадной кривой Коха - мера изрезанности этой кривой”.
Итак, Мандельброт превратил "монстров" из "пугал", за которыми надо было охотиться с целями исключения из "нормальных" геометрических рассуждений в концептуально оформленные геометрией предметы измерения и построения.
Этот же мыслительный ход можно осуществить и по отношению к парадоксам.
Действуя по аналогии, можно предположить, что парадоксы есть частные случаи логических фракталов, которыми должна оперировать фрактальная логика.
Мы сознательно не будем жестко определять термины "логический фрактал" и "фрактальная логика", постепенно вводя представления о частных случаях логических фракталов и соответствующих логик. Пока ограничимся представлением о том, что фрактальная логика – это набор понятий и представлений, основанных на принципах фрактальной геометрии, применяемых к логическим объектам с бесконечным количеством значений.
Фрактальная геометрия оперирует парадоксальными геометрическими предметами, результаты измерения которых (длина, площадь, объем) устремляются к бесконечности. В качестве начальной (а потому неточной) метафоры можно сказать, что фрактальная логика оперирует парадоксальными логическими объектами, число логических значений которых также стремится к бесконечности.
Фрактальная логика превращает бесконечный парадокс из «монстра» и «пугала» в концептуальный предмет формального, инструментального и социокультурного рассмотрения.
Для того, чтобы сделать термины "логический фрактал" и "фрактальная логика" не только метафорами, но и понятиями оформленной и формализованной логической концепции, рассмотрим понятие обратной связи.
Интерпретация построения “монстров” – фракталов через обратную связь содержится в книге Пайтгена, Юргенса и Заупе “Хаос и фракталы: новые горизонты науки”[16].
Российский математик Александр Зенкин[17] интерпретировал парадокс лжеца как процесс с обратной связью.
В свое время Алан Тьюринг предложил свой знаменитый мысленный эксперимент – машину Тьюринга, и выдвинул тезис о том, что любая вычислимая (частично рекурсивная – имеющая завершение) функция может быть запрограммирована (вычислена с помощью конечного алгоритма) на машине Тьюринга. Интеллект человека, по мнению Тьюринга, устроен похожим образом, поэтому машина в принципе может мыслить.
Машину Тьюринга можно интерпретировать в терминах отрицательной обратной связи – вычислительные процедуры за конечное число шагов сходятся к нужному значению функции.

Рис. 1.6.1 Алан Матисон Тьюринг (1912-1954)
Автор оригинальных трудов по математической логике, вычислительной математике, искусственному интеллекту. В годы второй мировой войны, будучи в Англии, успешно работал над дешифровкой сообщений нацистского командования.
Для систематизации и сравнения процедур генерации “монстров” и парадоксов, мы рассмотрим нечто подобное: мысленный эксперимент - машину логической обратной связи, схема которой представлена ниже.

блок
управления
 | |||
 |



 входной блок блок обработки выходной блок
входной блок блок обработки выходной блок
 | |||
 |
линия обратной связи
 |
Рис 1.6.2 Машина обратной связи.
Машина состоит из трех блоков памяти: входного блока (ВХБ), выходного блока (ВБ), блока управления (БУ) и одного процессорного блока обработки (БО), связанных между собой связями. Блок управления нужен для “запуска” машины.
Общая схема работы состоит из двух циклов – цикла запуска машины и рабочего цикла:
Цикл запуска:
1. Ввод информации в блок управления
2. Ввод информации во входной блок
3. Пересылка информации из блока управления в блок обработки
Рабочий цикл:
1. Пересылка информации из входного блока и ввод ее в блок обработки
2. Работа блока обработки
3. Пересылка информации из блока обработки в выходной блок
4. Пересылка информации из выходного блока во входной блок.
В качестве примера работы логической машины с обратной связью, приведем рассмотренный выше пример генерации кривой Коха:
1. Цикл запуска – в блок управления вводится “затравка” – единичный отрезок. Это нулевая итерация нашей фигуры – i=0.
2. Запускается рабочий цикл: затравка преобразуется в блоке обработки в первое поколение фигуры - отрезок делится на три равные части, средняя часть отбрасывается, а на ее месте строится ломаная, являющаяся фрагментом равностороннего треугольника со стороной, равной, одной третьей длины отрезка. Это первая итерация нашей фигуры – i=1.
3. Полученное первое поколение “отправляется” на выходной блок,
4. Обратная связь переносит первое поколение на вход.
После этого по тому же алгоритму, примененному для отдельному отрезку звеньев ломаной, первое поколение преобразуется во второе поколение в рабочем блоке: i=2.
Получающийся “монстр” – результат бесконечного числа циклов работы машины при i®¥.
В устремлении процедуры на бесконечность состоит главное отличие нашей машины от машины Тьюринга. Построение фракталов всегда осуществляется не на конечном, а на бесконечном числе итераций.
Теперь интерпретируем с помощью обратной связи парадокс лжеца.
Рассмотрим высказывание А, соответствующее суждению “Я лгу”.
Пусть оно будет истинным. С точки зрения обратной связи это означает, что на нулевой итерации при i=0, значение А равно И.
Далее, нам надо интерпретировать парадоксальное умозаключение “Значение А истинно, значит, А ложно” как обратную связь – процедуру, присваивающую новое значение высказыванию А при изменении счетчика итераций.
Обратная связь меняет значение А при i=1 на Л. Таким же образом, при i=2 значение А равно И, при i=3, опять Л – и так далее.
Таким образом, цикл запуска будет следующим:
Ввод информации в блок управления – установление i=0,.
Ввод информации во входной блок - значение А есть И
Пересылка информации из блока управления в блок обработки
Рабочий цикл:
Пересылка информации из входного блока и ввод ее в блок обработки
Работа блока обработки – смена значения А на противоположное (с И на Л или с Л на И), увеличение значения счетчика итераций на единицу,
Пересылка информации из блока обработки в выходной блок.
Пересылка информации из выходного блока во входной блок.
Построим таблицу истинности высказывания А в зависимости от итераций - различных i:
| i = 0 | i = 1 | i = 2 | i = 3 | i = 4 | I = 5 | i = 6 | i = 7 | i = 8 | … |
| И | Л | И | Л | И | Л | И | Л | И | … |
Таблица 1.6.1 Таблица истинности парадокса лжеца
Парадокс – это результат бесконечного изменения логического значения машиной обратной связи.
Таким образом, математический “монстр” и логический парадокс лжеца могут быть представлены как результат бесконечного числа итераций машины обратной связи.
На основании этой общности мы будем постепенно вводить представление о логических фракталах.
Date: 2015-06-05; view: 564; Нарушение авторских прав