Формализм масштабного преобразования. Преобразованный логический фрактал

n-мерное масштабное преобразование – унарная операция - преобразование данного логического ряда (затравки) в новый логический ряд путем последовательной замены кортежей длиной n затравки на новые кортежи.

Масштабное преобразование должно быть задано на всем наборе возможных значений кортежей длиной n для данной k-значной логики. Полученный новый логический ряд так же может подвергаться масштабному преобразованию либо конечное число раз, либо до бесконечности.

Заметим, что масштабное преобразование можно интерпретировать в терминах обратной связи, рассмотренной в 1.4 – преобразование последовательно применяется к уже преобразованному этим преобразованием логическому ряду. Ясно, что эта обратная связь отличается от обратной связи – генератора логического ряда через итерации начальных условий.

Обозначим две задачи масштабного преобразования. Прямая задача масштабного преобразования – по заданной затравке и масштабному преобразованию описать результат преобразований через заданное конечное число преобразований или бесконечное число преобразований.

Обратная задача масштабного преобразования – по заданному ряду реконструировать множество затравок и соответствующие им масштабные преобразования.

Будем обозначать преобразование кортеж затравки в кортеж нового ряда знаком решетки – “#”. Назовем это преобразование на отдельном кортеже решеткой. Количество решеток R в преобразовании рассчитывается по формуле: R=kⁿ, где k – количество значений в логике (для ЛКР это 2, для ЛРР это 3 и т.п.), n – длина кортежа.

Пример масштабного преобразования затравки иллюстрирован рисунком 2.5.1.

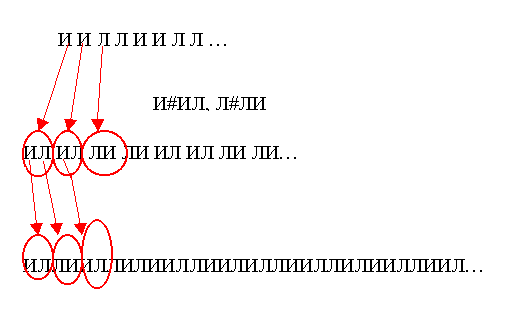
Рисунок 2.5.1 Схема масштабного преобразования затравки.

Масштабное преобразование чем-то напоминает сокращения в языке. Хофштадтер[19] (в блестящем переводе Марины Эскиной) рассмотрел следующее суждение: «БОГ, одолевающий гения», где слово «БОГ» – сокращение слов «БОГ», «Одолевающий», «Гения». При последовательной расшифровке сокращений получаем бесконечно разворачивающуюся последовательность суждений, в которых слово «БОГ» оказывается бесконечным сокращением самого себя. Интересно, что в этом случае обозначает слово БОГ?

Рассмотрим одномерное масштабное преобразование кортежей затравки в ЛКР. Набор значений унарных кортежей: И, Л. Поэтому для осуществления преобразования необходимы две решетки. В качестве примера можно взять следующий вариант преобразования:

И#ИЛ, Л#ЛЛ (2.4.1)

Это одномерное масштабное преобразование – преобразование унарных кортежей в бинарные кортежи.

Возможны и другие преобразования. Например:

И#ИЛЛЛЛИИ, Л#ЛИ (2.4.2)

Рассмотрим двухмерное масштабное преобразование. Весь набор бинарных кортежей следующий: <ИИ>, <ИЛ>, <ЛИ>, <ЛЛ>. Для осуществления преобразования необходимы четыре решетки. В качестве примера можно взять следующий вариант преобразования:

ИИ#Л, ИЛ#ЛЛЛИИИ, ЛИ#ИИ, ЛЛ#ИИИИИИИИИИЛ (2.4.3)

Вот еще один вариант:

ИИ#Л, ИЛ#Л ЛИ#И, ЛЛ#И (2.4.4)

Это – двухмерное масштабное преобразование – преобразование бинарных кортежей унарными кортежами.

Рассмотрим отдельную решетку в n-мерном масштабном преобразовании. Пусть минимальное количество значений в преобразовании справа от всех решеток – f, максимальное – s.

Если во всех решетках преобразования n<f, то такое преобразование мы будем называть расширение n-ок кортежей. Если во всех решетках преобразования n>s, то такое преобразование будем называть сжатие n-ок кортежей.

Масштабные преобразования (2.4.1) и (2.4.2) являются расширениями унарных кортежей. Масштабное преобразование (2.4.4) – сжатием бинарных кортежей. Масштабное преобразование (2.4.3) – не является расширением или сжатием.

Пример 2.4.1.

Возьмем ИРЛ в качестве затравки, и зададим для нее расширение унарных кортежей: И#ИЛИ, Л#ИИЛ.

Выпишем получившиеся ряды, последовательно их нумеруя:

Затравка: И Л И Л …

1: ИЛИ ИИЛ ИЛИ ИИЛ …

2: ИЛИ ИИЛ ИЛИ ИЛИ ИЛИ ИИЛ ИЛИ ИИЛ ИЛИ ИЛИ ИЛИ ИИЛ …

3: ИЛИ ИИЛ ИЛИ ИЛИ ИЛИ ИИЛ ИЛИ ИИЛ ИЛИ ИЛИ ИИЛ ИЛИ ИЛИ ИИЛ ИЛИ ИЛИ ИЛИ ИИЛ…

Пример 2.4.2

Зададим для ряда 3 из предыдущего примера сжатие бинарных кортежей:

ИИ#Л, ИЛ#И, ЛИ#И, ЛЛ#И.

Выпишем получившиеся логические ряды:

Затравка: ИЛ ИИ ИЛ ИЛ ИИ ЛИ ИЛ ИИ ИЛ ИЛ ИИ ИЛ ИЛ ИИ ЛИ ИИ ЛИ ЛИ ИЛ ИИ ИЛ ИЛ ИИ ЛИ ИЛ …

1: ИЛ ИИ ЛИ ИЛ ИИ ЛИ ИЛ ИЛ ИИ ИЛ ИИ ЛИ…

2: ИЛ ИИ ЛИ ЛЛ ЛИ ЛИ…

3. ИЛ ИИ ИИ…

Введем обозначение n-мерных масштабных преобразований по следующему принципу: 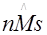, где s – порядковый номер масштабного преобразования. Ясно, что для любой n количество масштабных преобразований бесконечно.

Преобразованным логическим фракталом мы будем называть ряд, полученный в результате масштабного преобразования кортежей затравки неединичными кортежами, содержащими разные логические значения. Масштабное преобразование может осуществляться конечное или бесконечное число раз.

Соответственно если такой ряд является результатом бесконечного числа преобразований, то это бесконечно преобразованный логический фрактал. Если ряд является результатом s преобразований кортежей затравки, то это s-преобразованный логический фрактал.

Ясно, что если преобразование будут содержаться одинаковые логические значения, то в результате мы получим ЛВР или ИВР.

Теорема масштабного преобразования.

Если в n-мерном преобразовании справа от решеток стоят кортежи с одинаковой длиной не равной n и нетождественными логическими значениями внутри кортежа, то получившийся в результате хотя бы одного такого преобразования ряд является регулярным логическим фракталом.

Доказательство.

Пусть справа от решеток в преобразовании стоит q кортежей. Рассмотрим затравку – ряд А и результат преобразования – ряд В.

У ряда В есть два тождественных масштаба – с разрешением n и с разрешением s.

Так как логические значения внутри кортежей разные, то ряд В не является тривиальным. Поэтому, по определению, ряд В является логическим фракталам.

Теорема доказана.

Пример.

Рассмотрим затравку – ИВ.

Зададим преобразование:

И#ИЛ, Л#ИЛ

В результате получим последовательность рядов:

ИИИИИИИИ…

ИЛИЛИЛИЛ…

ИЛИЛИЛИЛ…

…

В результате бесконечного числа преобразований мы получаем ИРЛ, который является регулярным фракталом, бесконечно преобразованным фракталом из затравки ИВ и s-преобразованным логическим фракталом из затравки ИВ где s – целое положительное число.