Линейные непрерывные детерминированные системы

Уравнение состояния линейной непрерывной детерминированной системы при 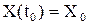имеет вид:

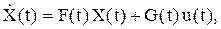(4.6)

где F(t) – матрица коэффициентов размерности 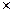n n;

G(t) – вектор коэффициентов (n-мерный);

u(t) – входное воздействие.

Вектор состояния X(t) определяется путем решения уравнения состояния (4.6):

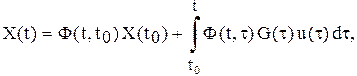(4.7)

где Ф(t,t₀) – переходная матрица состояний размерности 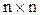, которая определяется путем решения дифференциального уравнения

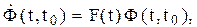(4.8)

при начальных условиях:

Ф(t₀, t₀) = I, (4.9)

где I – единичная матрица, и замене t₀ на τ.

Стационарная физическая система. Уравнение состояния стационарной системы имеет вид:

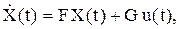(4.10)

где F и G не зависят от времени.

Решение уравнения (4.10) значительно упрощается.

Переходная матрица состояний определяется так:

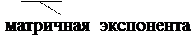
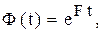(4.11)

где

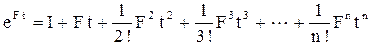− (4.12)

экспоненциальный ряд.

Тогда

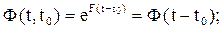(4.13)

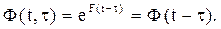(4.14)

Решение динамической модели (4.10) запишется в виде:

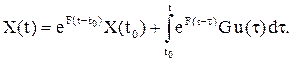(4.15)

При определении матричной экспоненты можно ограничиться первыми четырьмя членами ряда (4.12), что обеспечит достаточную точность результата при малых значениях .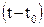

Date: 2015-05-23; view: 786; Нарушение авторских прав