
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сглаживание временных рядов
|
|
Наиболее распространенные методы изучения тренда:
· укрупнение интервалов;
· сглаживание скользящей средней;
· нахождение регрессионных зависимостей:
· использование математических фильтров и т.д.
Метод укрупненных интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывaющих основную тенденцию развития. Идея этого метода заключается в преобразовании первоначального ряда динамики в ряды средних значений за более продолжительные периоды (месячные - в квартальные, квартальные - в годовые и т.д.). В результате укрупнения интервалов общая тенденция роста продажи становится очевидной.
Разновидностью метода укрупнения интервалов является метод сглаживания (скользящей средней). Сущность сглаживания методом скользящей средней состоит в том, что по исходным уровням ряда (эмпирическим данным) определяют расчетные (теоретические) уровни, чаще всего в виде среднего значения. Определив среднее значение исследуемой величины на некотором первоначальном интервале (это не обязательно должен быть квартал, полугодие, год), рассматриваемый интервал сдвигается (скользит) на одно наблюдение. То есть если первоначальный интервал составлял январь-апрель некоторого года, то следующий рассматриваемый интервал будет февраль-май того же года. В результате на рассматриваемых временных интервалах случайные тенденции погашаются, а основная тенденция развития выражается в виде плавной линии.
Для определения тренда на основе анализа скользящей средней можно сделать вывод о том, что удобнее тренд представить либо в виде прямой, линейной зависимости результирующего показателя от времени, либо в виде полинома второй или третьей степени.
Особенность исследования товарооборота заключается в том, что на динамику товарооборота большое влияние оказывает сезонная составляющая.
Полученная зависимость будет представлять собой вклад сезонной составляющей в общее изменение товарооборота.
Для измерения тренда используется метод аналитического выравнивания. Основным содержанием этого метода является то, что основная тенденция развития yt рассчитывается как функция времени yti= f(ti).
Определение теоретических уровней уti производится на основе так называемой адекватной математической функции. Подбор адекватной функции производится методом наименьших квадратов – минимальностью отклонений суммы квадратов между теоретическими и эмпирическими уровнями товарооборота, т.е.
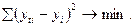
Важнейшей проблемой является подбор математической функции, по которойрассчитываются теоретические уровни тренда. В практике изучения тренда различают следующие эталонные типы развития товарооборота во времени, в основе которых лежат абсолютные приросты, относительные приросты и темпы роста:
1. Равномерное развитие – линейная форма тренда применяется для рядов динамики со стабильными абсолютными приростами 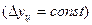 . Основная тенденция развития отображается уравнением прямолинейной функции:
. Основная тенденция развития отображается уравнением прямолинейной функции: 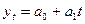 . Параметр а1 является коэффициентом регрессии, определяющим направление развития. Если а1>0, то уровни ряда динамики возрастают, если а1<0 – равномерно снижаются;
. Параметр а1 является коэффициентом регрессии, определяющим направление развития. Если а1>0, то уровни ряда динамики возрастают, если а1<0 – равномерно снижаются;
2. Равноускоренное (равнозамедленное) развитие – параболическая форма тренда – применяется для рядов динамики со стабильными темпами прироста (Тпр = const). Основная тенденция развития отображается функцией параболы второго порядка
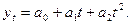
Параметр а2 характеризует постоянное изменение интенсивности развития (в единицу времени). При а2 >0 происходит ускорение развития, а при а2<0 – идет процесс замедления роста;
3. Развитие с переменным ускорением (замедлением) отображает функции параболы 3-его порядка
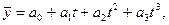
где а3 – отображает изменение ускорения, (при а3>0 – ускорение возрастает, а3<0 – ускорение замедляется);
4. Развитие по экспоненте. Экспоненциальное сглаживание временных рядов – модификация метода наименьших квадратов для анализа временных рядов, при котором более поздним наблюдениям придается большой вес, иными словами веса точек ряда убывают (экспоненциальный закон) по мере удаления в прошлое.
Этот тип динамики характеризуют стабильные темпы роста
Трц 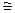 const.
const.
Основная тенденция в рядах динамики с постоянными темпами роста отображается показательной функцией
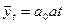
где а – темп роста (снижения) изучаемого явления в единицу времени, т.е. интенсивность развития;
5. Развитие с замедлением роста в конце периода. У этого типа динамики показание цепного абсолютного прироста сокращается в конечных уровнях ряда динамики Dуцп 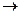 0 (достижение насыщения).
0 (достижение насыщения).
Основная тенденция развития в таких рядах динамики выражается полулогарифмической функцией:
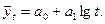
Практика статического изучения тренда социально-экономических явлений показывает, что чаще невозможно однозначно решить вопрос, какому виду развития больше всего отвечают показатели динамики. Реальные условия формирования показателей товарооборота предполагают изменение товарооборота под влиянием множества факторов разнонаправленного действия, поэтому трудно найти адекватную форму связи.
Для подтверждения гипотезы о возможном типе развития можно использовать графический метод. Наглядное изображение тренда можно получить по расположению на поле графика эмпирических уровней. Но график не может дать обобщенную оценку выявленного тренда.
Для определения параметров математических функций при анализе тренда используется способ отсчета времени от условного начала. Он основан на обозначении в ряду динамики показателей времени таким образом, чтобы St=0.
При этом в ряду динамики с нечетным числом уровней порядковый номер уровня, находящегося в середине ряда, обозначают через нулевое значение и принимают его за условное начало отсчета времени, + 1 для всех последующих уровней и – 1 – для предыдущих.
При четном числе уровней порядковые номера верхней половины обозначаются -1, -3, -5…, а для нижней половины +1, +3, +5…
Тогда параметры уравнений определяются по формулам:
а) для прямолинейной функции
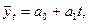
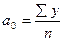 ,
, 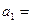

б) для показательной функции
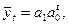
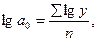
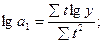
в) для параболы 2-го порядка
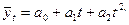
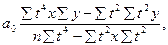
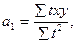
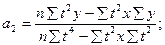
г) для параболы 3-его порядка
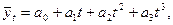
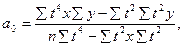
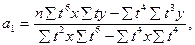
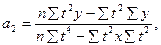

Рассмотрим пример – изменение товарооборота конкретного торгового предприятия
Методика анализа динамики товарооборота и сезонных колебаний рассматривается на примере торгового предприятия по мелкооптовой продаже продовольственных товаров.
Для выявления общей тенденции развития товарооборота проводится анализ динамических рядов за 2005-2007 гг. Фактические уровни товарооборота приведены к сопоставимому виду с учетом индекса потребительских цен на товары.
В ходе анализа рассчитываются абсолютные приросты, темпы роста в % и темпы прироста цепные и базисные.
Результаты расчетов представлены в табл. 1. Из расчетов следует, что по сравнению с 1 кварталом в каждом последующем периоде происходило увеличение товарооборота, за исключением III квартала 2006 г., в котором товарооборот снизился на 2,3 млн. руб. по сравнению с I кварталом 2006 г.
Таблица 1. Расчет абсолютных и относительных показателей ряда динамики
| Период | Товарооборот млн. руб. | Абсолютный прирост, млн.руб. | Темп роста, % | Темп прироста, % | |||
| базисный | цепной | базисный | цепной | базисный | цепной | ||
| I - 2005 | 200.7 | - | - | - | - | - | - |
| II - 2005 | 230.2 | 29.5 | 29.5 | 114.7 | 114.7 | 14.7 | 14.7 |
| III- 2005 | 198.4 | -2.3 | -31.8 | 98.9 | 86.2 | -1.1 | -13.8 |
| IV- 2005 | 327.2 | 126.5 | 128.8 | 163.1 | 164.5 | 63.1 | 64.5 |
| I -2006 | 247.8 | 47.1 | -79.4 | 123.5 | 75.5 | 23.5 | -24.5 |
| II-2006 | 227.1 | 26.4 | -20.7 | 113.2 | 91.6 | 13.2 | -8.4 |
| III- 2006 | 264.4 | 63.7 | 37.3 | 131.7 | 116.4 | 31.7 | 16.4 |
| IV-2006 | 287.1 | 86.4 | 22.7 | 108.8 | 8.6 | ||
| I – 2007 | 230.9 | 30.2 | -56.2 | 123.4 | 23.4 | ||
| II- 2007 | 234.8 | 34.1 | 3.9 | 101.7 | 1.7 | ||
| III- 2007 | 289.5 | 88.8 | 54.7 | 144.2 | 123.3 | 44.2 | 23.3 |
| IV- 2007 | 383.7 | 94.2 | 191.2 | 132.6 | 91.2 | 32.6 |
Анализ результатов расчетов по табл. 1 показывает, что тенденция роста не является устойчивой, т.к. из 12 анализируемых кварталов товарооборот снижается, в остальные периоды возрастает. Средний абсолютный прирост составил:
D 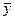 = 16,64 млн.руб.
= 16,64 млн.руб.
Визуальный анализ рассчитанных показателей динамики не дает достаточных оснований для выбора той или иной динамической модели.
Для выявления общей тенденции развития товарооборота воспользуемся методом укрупнения интервалов и сглаживания ряда с помощью скользящей средней.
Метод укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Этот метод основан на укрупнении периодов, к которым относятся уровни ряда динамики. Для этой цели исходные (квартальные) данные об объеме товарооборота преобразуем в полугодовые.
Результаты укрупнения приведены в табл.2
Таблица 2. Определение общей тенденции товарооборота
методом укрупнения интервалов, млн. руб.
| I полугодие 2005г. | I I полугодие 2005г. | I полугодие 2006г. | I I полугодие 2006г. | I полугодие 2007г. | I I полугодие 2007г. |
| 430,9 | 525,6 | 474,9 | 551,5 | 465,7 | 673,2 |
В результате укрупнения интервалов общая тенденция развития товарооборота становится более очевидной. Из таблицы видно, что в первом полугодии товарооборот ниже, чем во втором (за все 3 года).
Расчет методом сглаживания скользящей средней представлен в табл. 3.
Таблица 3. Расчет скользящих средних
| Год, квартал | Исходные уровни | Скользящие средние | Сглаженные уровни с центрированием |
| 2005г. I кв. | 200, 7 | ||
| II кв. | 230,2 | 956,5: 4 = 239,1 | |
| III кв. | 198,4 | 1003,6: 4 = 250,9 | 490: 2 = 245 |
| IV кв. | 327,2 | 1000,5: 4 =250,1 | 501:2 = 250,5 |
| 2006 г. I кв. | 247,8 | 1066,5: 4 = 266,6 | 516,7: 2 = 258,4 |
| II кв. | 227,1 | 1026,4: 4 = 256,6 | 523,2: 2 = 261,6 |
| III кв. | 264,4 | 1009,5: 4 = 252,4 | 509: 2 = 254,5 |
| IV кв. | 287,1 | 1017,2: 4 = 254,3 | 506,7: 2 = 253,4 |
| 2007 г. I кв. | 230,9 | 1042,3: 4 = 260,6 | 514,9: 2 = 257,5 |
| II кв. | 234,8 | 1138,9: 4 = 284,7 | 545,3:2 = 272,7 |
| III кв. | 289,5 | ||
| IV кв. | 383,7 |
Анализ сглаженных уровней выявляет общую тенденцию роста товарооборота, но в течение анализируемого периода наблюдаются колебания объема продаж в сторону увеличения или уменьшения. Так, с начала 2006г. до середины 2008 г. товарооборот растет, затем снижается и вновь возрастает.
Применение в анализе рядов динамики методов укрупнения интервалов и скользящей средней позволяет выявить тренд для его описания, но получить обобщенную оценку тренда с помощью этих методов невозможно. Измерение тренда достигается с помощью метода аналитического выравнивания. Исследуемые динамические ряды товарооборота не имеют явной тенденции к росту, спаду или постоянству, и форма связи неочевидна. В этом случае расчет модели производится с применением нескольких уравнений регрессии.
Для измерения тренда воспользуемся двумя функциями:
1) прямолинейной функцией
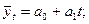
2) функцией параболы второго порядка
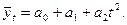
Данные для расчета параметров прямолинейной функции и теоретические значения товарооборота представлены в таблице 4.
Таблица 4. Построение динамических рядов товарооборота
в виде прямолинейной функции, млн. руб.
| Период | y | t | 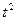
| t x y | 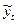 
|
| I - 2005 | 200.7 | -6 | -1204.2 | 215.1 | |
| II - 2005 | 230.2 | -5 | -1151 | 222.6 | |
| III- 2005 | 198.4 | -4 | -793.6 | 230.1 | |
| IV- 2005 | 327.2 | -3 | -981.6 | 237.6 | |
| I -2006 | 247.8 | -2 | -495.6 | 245.1 | |
| II-2006 | 227.1 | -1 | -227.1 | 252.7 | |
| III- 2006 | 264.4 | 264.4 | 267.7 | ||
| IV-2006 | 287.1 | 574.2 | 275.2 | ||
| I – 2007 | 230.9 | 692.7 | 282.7 | ||
| II- 2007 | 234.8 | 939.2 | 290.2 | ||
| III- 2007 | 289.5 | 1447.5 | 297.7 | ||
| IV- 2007 | 383.7 | 2302.2 | 305.2 | ||
| Итого | 3121,8 | 1367,1 | 3121,9 |
Параметры уравнения а 0 и а1 находятся по следующим формулам:
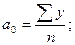
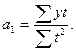
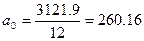 ;
; 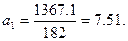
Получаем прямолинейную функцию:
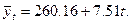
Подставляя последовательно значения времени t, получим теоретические уровни товарооборота. Ошибка аппроксимации для прямолинейной формы тренда составит:
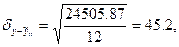

Далее предположим, что тренд товарооборота приближается к функции параболы второго порядка:
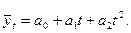
Параметры уравнения а0, а1 и а2 находим из системы нормальных уравнений, при Σt = 0 значения параметров рассчитываются по формулам:
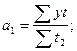
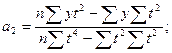

Расчет параметров уравнения производится по данным таблице 5.
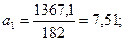
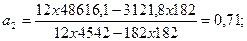
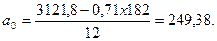
Таблица 5 Построение динамических рядов товарооборота
в виде параболы второго порядка, млн. руб.
| Период | Товарооборот (у) | t | 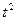
| 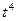
| t x y | t2 x y | 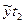
|
| I - 2005 | 200.7 | -6 | -1204.2 | 7225.2 | 229.9 | ||
| II - 2005 | 230.2 | -5 | -1151 | 229.6 | |||
| III- 2005 | 198.4 | -4 | -793.6 | 3174.4 | 230.7 | ||
| IV- 2005 | 327.2 | -3 | -981.6 | 2944.8 | 233.2 | ||
| I -2006 | 247.8 | -2 | -495.6 | 991.2 | 237.2 | ||
| II-2006 | 227.1 | -1 | -227.1 | 227.1 | 242.6 | ||
| III- 2006 | 264.4 | 264.4 | 264.4 | 257.6 | |||
| IV-2006 | 287.1 | 574.2 | 1148.4 | 267.2 | |||
| I – 2007 | 230.9 | 692.7 | 2078.1 | 278.3 | |||
| II- 2007 | 234.8 | 939.2 | 3756.8 | 290.8 | |||
| III- 2007 | 289.5 | 1447.5 | 7237.5 | 304.7 | |||
| IV- 2007 | 383.7 | 2302.2 | 13813.2 | ||||
| Итого | 3121.8 | 1367.1 | 48616.1 | 3121.8 |
Получаем уравнение параболы второго порядка:
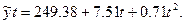
Последовательно подставляя значения времени t и 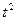 , получим теоретические значения
, получим теоретические значения 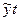 .
.
Далее рассчитаем ошибку аппроксимации, для функции тренда в виде параболы второго порядка по формуле:


Сравнивая коэффициенты аппроксимации, видим, что ошибка меньше при выражении динамики товарооборота в виде параболы второго порядка, значит, эта модель более адекватно описывает динамику развития товарооборота.
Date: 2015-05-23; view: 1321; Нарушение авторских прав