Групповое принятие решений

Решение в группах можно принимать на основе разных правил: от демократических до силовых. Если решение формируется на демократической основе, когда все индивиды равны, требуется построение специальных правил, позволяющих обнаружить общие предпочтения. Примеры такой группы - законодательное собрание, общество, группа экспертов. Наиболее распространенный метод большинства голосов может привести к тому, что будет отклонена более предпочтительная кандидатура, если выборы проводятся в два тура.

Для учета такой информации, можно было бы провести ранжировку кандидатов. Предположим, что такие ранжировки реализуемы. Пусть получены ранжировки от каждого избирателя. Как выявить победителя. Формализуем эту задачу: имеется множество лиц (I), занумерованных числом от 1 до t. Элементами множества А являются некоторые объекты, альтернативы и т. д. Обозначим Р_i ранжировку альтернатив из А, указанную i-м индивидом. Для альтернатив a, b из А запись aР_ib означает, что i-ый индивид ставит a на более высокое место. В таких ранжировках допускается связи. Если a, b считаются i-ым индивидом связанными, то будем записывать aT_ib. В частности, если ранжировка проводилась по отношению предпочтения, то T_i – отношение безразличия. Рассмотрим пример ранжировки A={x,y,u,v}. P_i – ранжировка имеет вид: x; y-v; u (y, v – неразличимы для I-го индивида). Ранжировка является строгим слабым порядком. Каждая ранжировка транзитивна и асимметрична. Набор ранжировок p₁, p₂, …, p_n, отражающих предпочтение членов группы, определяет групповой профиль. Обозначим 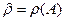– совокупность всех возможных ранжировок А. Пусть 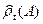– произведение сомножителей: 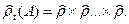Тогда 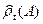обозначает совокупность всех профилей группы из t индивидуумов на множестве А.

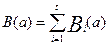Нас интересует проблема: как найти по данному профилю p₁, …, p_t выигравшую альтернативу или как найти ранжировку, которая выражает согласованное мнение группы. В частности, если каждое P_i получается в результате упорядочивания по предпочтению, то P представляет собой групповое предпочтение, тогда по такой ранжировке можно выявить победителя. Но возникает проблема построения такой ранжировки. Правило построения групповой ранжировки по групповому профилю называют групповой функцией согласования. Если ранжировки отражают предпочтения, а множество I – это все общество, то говорят о функции общественного выбора. Групповую функцию согласования можно представить как функцию F. Возникает задача, какие функции F можно считать разумными. Самое очевидное – это правило простого большинства. Если Р₁, Р₂, …, Р_t –профиль группы, то альтернатива а получает более высокое место, чем альтернатива b тогда и только тогда, когда большинство оценивает а выше b. Объединение ранжировок по правилу простого большинства не обязательно приводит к групповой ранжировке (парадокс Кондорсе). Более того, по определению групповой функции согласования, правило простого большинства не всегда создает такую функцию, т. к. не всякому профилю можно сопоставить ранжировку. Но можно построить функцию группового выбора, соотносящей каждому профилю допустимую ранжировку. Например, правило Борда: пусть величина В_i(а) равна числу альтернатив, расположенных ниже альтернативы а в ранжировке P_i, и

Величину В(а) называют числом Борда для альтернативы а. Тогда можно определить функцию выбора Борда в групповом предпочтении. Альтернатива а выше b тогда и только тогда, когда В(а) больше В(b).

Правило Борда всегда приводит к ранжировке, но она не всегда согласуется с нашим интуитивным представлением о справедливости.

Рассмотрим следующий профиль: Р₁, Р₂, …, Р₅.

Р₁: x, y, z, u, v, w

P₂: x, y, z, u, v, w

P₃: x, y, z, u, v, w

P₄: x, y, z, u, v, w

P₅: y, z, u, v, w, x

B₁(x)=5*4, B₁(y)=4*4=16,

B₅(x)=0, B₅(y)=5,

B(x)=20 B(y)=21, очевидно x выше, но правило Борда выбирает y.

Хотя существует много функций группового выбора, для любой можно построить примеры, неприемлемые с определенной точки зрения, поэтому определить какая из двух функций более обоснована очень сложно. В этих обстоятельствах подход к решению состоит в следующем: сначала выписываются условия, которым должна удовлетворять функция группового выбора, а затем выявляют, можно ли из них вывести такую функцию или класс таких функций. Таким свойством обладает аксиоматический подход.

Оказывается, выбрать обоснованно функцию выбора невозможно.

Рассмотрим теорему Эрроу о невозможности:

В аксиомах Эрроу формируются условия, которым должна удовлетворять разумная функция группового выбора.

Аксиома 1: (положительная связь групповых и индивидуальных предпочтений)

Если функция группового выбора определяет по данному профилю, что а предпочтительнее b, то это предпочтение сохраняется, если профиль изменить следующим образом:

а) индивидуальные предпочтения для пар альтернатив, отличных от а не меняются;

б) индивидуальные предпочтения для а и любой другой альтернативы могут измениться только в пользу а.

Аксиома 2: (независимость несвязанных альтернатив)

Пусть А₁ – произвольное подмножество альтернатив А. Если при изменении профиля индивидуальные предпочтения среди элементов А сохраняются, то групповые предпочтения, получающиеся для исходного и измененного профиля на альтернативах А₁ должны совпадать.

Аксиома 3: (суверенность граждан)

Для каждой пары альтернатив а и b существует профиль, для которого в групповой ранжировке а предпочтительнее b.

Если бы эта аксиома не выполнялась, то нашлась бы пара таких альтернатив a и b, что независимо от индивидуальных предпочтений, даже если для каждого индивидуума a предпочтительнее b, в групповой ранжировке альтернатива a никогда не была бы предпочтительнее b. В этом случае результат общественного сравнения a и b навязан группе и предпочтения индивидуумов не играют никакой роли. Эта аксиома удовлетворяется при выполнении следующего условия: если каждый индивидуум ставит a предпочтительнее b, то для группы a предпочтительнее b.

Аксиома 4: (отсутствие диктатора)

В группе нет такого индивидуума, что если для него a предпочтительнее b, при любых a и b из А, то и для группы a должен быть предпочтительнее b независимо от предпочтений других индивидуумов.

Если для j-го индивидуума аксиома 4 нарушена, то его можно назвать диктатором (лидером).

Выводы: для случая, когда имеется не менее трех альтернатив, а группа состоит хотя бы из двух индивидуумов, то справедлива:

Теорема Эрроу о невозможности:

Пусть множество альтернатив А содержит не менее трех элементов, число индивидуумов t не менее двух,

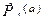- это множество всех профилей на А для группы из t индивидуумов. Тогда функции группового выбора, определенной на этом множестве и удовлетворяющей аксиомам 1-4 не существует.

Замечание: если функция группового выбора удовлетворяет аксиомам 1 и 2, то она либо навязана, либо диктаторская.

Причина ошибочности аксиомы 2 может быть связана с тем, что в рассмотрении используется свойство предпочтительности одной альтернативы над другой. Не существует универсального набора аксиом, не приводящего к трудностям при построении групповой функции выбора.

ЛИТЕРАТУРА

1. Системный анализ в экономике и организации производства. Под ред. Валуева С.А.-Л.: Политехника, 1991.

2. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ.-М.: Высшая школа, 1989.

3. Ларичев О.И. Теория и методы принятия решений. - М.: Логос, 2000.

4. Поспелов Г.С., Ириков В.А. Программно-целевое планирование и управление.- М:Сов.Радио, 1976.

5. Теория прогнозирования и принятия решений./ Под ред. С.А.Саркисяна – М.: Высшая школа, 1977.

6. Месарович М., Такахара И. Общая теория систем: математические основы.-М.: Мир, 1978.

7. Моисеев Н.Н. Математические задачи системного анализа. –М.: Наука, 1981.

8. Райфа Г. Анализ решений.- М.: Наука, 1977.

9. Саати Т., Кернс К. Аналитическое планирование. Организация систем. – М.: Радио и связь, 1991.

10. Черняк Ю.И. Системный анализ в управлении экономикой.- М.: Экономика, 1975.

11. Kendall K., Kendall J. System Analysis and Design. – New Jersey: Prentice – Hall, Inc., 1988.

12. Крушевский А.В. Справочник по экономико-математическим методам и моделям.- Киев: Техника, 1982.

СОДЕРЖАНИЕ

Системный анализ и задачи управления.............................................. 3

Применение системного анализа в экономике..................................... 6

Модели и моделирование..................................................................... 8

Принципы формирования информационных систем........................ 11

Влияние стиля организации на информационную систему............... 14

Подходы к построению ИС................................................................ 19

Определение системы.......................................................................... 28

Строение и функционирование системы............................................ 29

Структуры и формы их представления.............................................. 31

Закономерности сложных систем....................................................... 39

Закономерности формирования иерархической структуры целей... 41

Классификация методов и моделей системного анализа................... 42

МФПС.................................................................................................. 45

МАИС.................................................................................................. 47

Процедуры системного исследования................................................ 51

Основные этапы системного исследования........................................ 52

Понятие о методике системного анализа............................................ 53

МАИ..................................................................................................... 56

Проблема принятия решений............................................................. 62

Выбор решения в подходах КАР и ВАР........................................... 64

Групповое принятие решений............................................................ 65

ЛИТЕРАТУРА..................................................................................... 69

Учебное издание

Амбросов Николай Владимирович

Системный анализ в управлении

социально-экономической системой

Учебно-методическое пособие

ЛР №020262 от 10.11.96.

Подписано в печать. Формат 60х90 1/16. Бумага офсетная.

Печать трафаретная. Усл.печ.л. 4,5. Уч.-изд.л. 3,9. Тираж 100 экз.

Заказ.

Издательство Иркутской государственной экономической академии.

664015, Иркутск, ул. Ленина, 11.

Отпечатано в ИПО ИГЭА.

Date: 2015-05-23; view: 1071; Нарушение авторских прав