
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Введение 4 page
|
|
Количество информации, как и энтропия, измеряется в битах. Один бит информации – это количество информации, сообщающее о том, какое из двух равновероятных событий имело место. Например, количество информации, заключающееся в одной элементарной ячейке ЭВМ, содержащей либо 0, либо 1, составляет один бит.
Рассмотрим пример, в котором бы фигурировала апостериорная неопределенность. Пусть методом перебора вариантов ведется поиск корня некоторого уравнения с точностью до полуцелого числа. Предварительно известно, что значение корня находится в интервале от 1 до 100, так что следует перебрать 200 вариантов. Тогда неопределенность значения корня в равновероятном варианте (4.4) составит H = log2 200 = 13,3 бит.
Пусть проведена проверка 150 вариантов возможных значений корня, но корень не найден. Однако получена ли некоторая информация о значении корня? Несомненно, и чтобы ее определить, необходимо сначала найти остаточную (апостериорную) неопределенность: Н1 = log2 (200 – 150) = 5,6. Тогда искомое количество информации составит 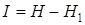 = 13,3 – 5,6 = 7,7 бит.
= 13,3 – 5,6 = 7,7 бит.
Условная энтропия. Рассмотрим понятие количества информации на примере передачи сигналов. Пусть передается группа сигналов азбукой Морзе:
· ¾ ¾ ¾ · ¾ ¾ · ¾
До получения очередного символа на приемном конце существует неопределенность «какой сигнал будет отправлен?» Эту неопределенность можно характеризовать энтропией «на один символ» (4.6) при числе исходов k = 3 (точка, тире, пробел) с вероятностями рi (i = 1, 2, 3). Вероятности появления на приемном конце точки, тире или пробела, т.е. вероятности (частоты) употребления символов конкретного языка специалистам известны из статистического анализа большого объема текстов на этом языке. Подсчитав энтропию на один символ, по формуле (4.6) легко определить общую энтропию сообщения (4.7). В данном примере 10 символов, включая пробел и, следовательно, N = 10.
Итак, на приемном конце до получения сообщения существовала априорная неопределенность (4.7) или на один знак (4.6). После получения сообщения неопределенность была устранена и получена информация I = H – 0.
Однако такая простая ситуация возникает, если сообщение передается без помех (канал без шума). Если имеется шум, то его действие приводит к тому, что переданный символ может либо остаться прежним (i-м), либо быть случайно подмененным любым другим (n-м) символом. Вероятность такой подмены по обозначению р(yn | xi), где х относится к переданному сигналу, а y к принимаемому сигналу в приемнике. В канале без помех yn = xi. Вероятность р(yn | xi) носит название условной вероятности xi) -–вероятность того, что отправленный i-й сигнал соответствует n-му сигналу на приемном конце. Конечно, эту ситуацию можно рассматривать и со стороны передатчика, используя условные вероятности вида р(xi|yn). В этом случае р(xi|yn) – вероятность того, что принятый на приемном конце n-й сигнал соответствует i-му сигналу на передающей стороне. Понятие условной вероятности вводит условную энтропию как функцию условной вероятности. В общем виде это записывается в следующих обозначениях:
I(X,Y) = H(X) – H(X½Y)
I(X,Y) = H(Y) – H(Y½X)
В этих идентичных выражениях условная энтропия играет роль апостериорной энтропии, а количество информации есть мера соответствия двух случайных объектов Х и Y.
Эта мера позволяет понять связь между понятием информации и её количеством. Информация есть отражение одного объекта другим. В данном примере такими объектами являются приемник и передатчик. Среднее же количество информации и есть числовая характеристика полноты этого отражения, степени соответствия, наконец, степени взаимодействия этих объектов. Но при взаимодействии объекты оказывают влияние друг на друга, и мы привыкли при этом различать причину и следствие. Количественное описание информации это другой тип описания взаимодействий, никак не связанный с классическими причинно-следственными описаниями. Такой тип связи характерен для НВТ.
Здесь полезно обратиться к п.3.6, где уже касались ограничений классического, причинно-следственного механизма при описании взаимодействий в открытой системе.
4.3.Энтропия непрерывного множества. Ранее была рассмотрена энтропия дискретного множества. Это означает, что подразумевались системы, где число возможных исходов (элементов множества) конечно. Однако приходится часто сталкиваться с ситуациями, когда число элементов может быть сколь угодно велико. Из теории вероятностей известно, что в этом случае следует иметь дело не с вероятностью отдельного исхода, которая равна нулю, а с плотностью распределения вероятности 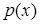 . Эта функция обладает таким свойством, что величина
. Эта функция обладает таким свойством, что величина 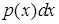 есть вероятность того, что интересующая нас переменная x (значение корня в примере п.4.2.) примет значения, заключенные в интервале от x до x+dx.
есть вероятность того, что интересующая нас переменная x (значение корня в примере п.4.2.) примет значения, заключенные в интервале от x до x+dx.
Теперь для оценки неопределенности необходимо прибегнуть к энтропии непрерывного множества, которая по аналогии с энтропией дискретного множества (4.5) имеет вид
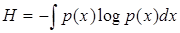 . (4.9)
. (4.9)
В качестве примера использования этой функции, попытаемся оценить неопределенность опыта, связанного со случайным поиском в заданном интервале значения корня (см. п.4.2) при отсутствии ограничения на точность поиска.
Повышая требования к точности ответа, можно ожидать сколь угодно большого числа возможных исходов опыта. При этом вероятность каждого исхода стремится к нулю, а искомый корень может принимать все возможные (бесчисленные) значения в заданном числовом интервале от 0 до 200. Попробуем использовать для этой же задачи энтропию непрерывного множества. Введем отрезок длиной l = x1 – x0 относительных единиц. Вероятность обнаружить значение корня на участке dx составляет dx/ 1. С другой стороны, эта же вероятность по определению 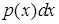 . Следовательно, для равновероятного случая
. Следовательно, для равновероятного случая 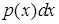 = dx / l и
= dx / l и 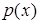 = 1/ l. Подставляя это значение в (4.), несложно получить H = log2l = 5,6 бит.
= 1/ l. Подставляя это значение в (4.), несложно получить H = log2l = 5,6 бит.
Сравним полученный результат с примером в п.4.2. В случае дискретного множества в энтропии используется число дискретных интервалов на выделенном отрезке, а в случае непрерывного множества – относительная длина самого отрезка. Заметим, что длина должна быть выражена в относительной форме, в противном случае под логарифмом появилась бы размерная величина. Масштаб приведения к относительной форме не имеет для информационной энтропии принципиального значения, поскольку с самого начала энтропия введена с точностью до множителя (до постоянной интегрирования, см процедуру интегрирования в п.4.1).
Энтропия непрерывного множества или дифференциальная энтропия (4.9) обладает большинством свойств энтропии дискретного множества.
В современной литературе можно встретить критику понятия дифференциальной энтропии и вытекающего из этого понятия дифференциального количества информации [21]. Эта критика по своему характеру совпадает с критикой концепции непрерывности, рассмотренной ранее в п.3.5.
4.4.Энтропия как мера разнообразия, неупорядоченности, хаоса. До сих пор понятие энтропии связывалось с неопределенностью. Энтропия допускает и другое толкование. Представим себе систему, состоящую из камеры, в которой находятся N шаров m типов, отличающихся, например, цветом. Предполагается, что N достаточно большое число. Обозначим долю шаров i -го типа (цвета) – 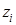
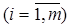 . Если произвести опыт над системой, заключающийся в извлечении наугад одного шара, то энтропия одного опыта согласно (4.6) составит:
. Если произвести опыт над системой, заключающийся в извлечении наугад одного шара, то энтропия одного опыта согласно (4.6) составит:
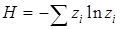 . (4.10)
. (4.10)
При этом принято, что размеры шаров одинаковы, в противном случае вероятность извлечения шаров i -того типа не будет точно соответствовать их доле в камере. Энтропия всех опытов над системой
 . (4.11)
. (4.11)
Поскольку правая часть последних выражений включает в себя параметры, характеризующие содержимое системы, то возникает вопрос, нельзя ли не обращаясь к опытам с шарами уяснить, с какой точки зрения эти функции характеризуют содержимое камеры.
Первая из двух функций характеризует степень неупорядоченности системы или степень разнообразия в ней с учётом выбранного признака для различения элементов системы (цвета шаров). Если бы в камере находились шары одного типа, тогда одно из значений вероятности p = z равнялось бы единице, а все остальные – нулю, и энтропия приняла бы нулевое значение. Это означало бы, что система полностью упорядочена, или, что то же самое – в системе отсутствует разнообразие по оцениваемому признаку (цвету).
Вторая функция (4.11) измеряет неупорядоченность (разнообразие) в системе несколько иначе. Отличие этих двух функций можно иллюстрировать следующим примером. Если камеру разделить на две части, то при достаточно большом количестве шаров в ней доля шаров i -го типа в каждой из двух частей останется прежней, но число шаров уменьшится вдвое, также вдвое уменьшится неупорядоченность, оцениваемая формулой (4.11). Однако степень неупорядоченности для каждой из двух частей, оцениваемая функцией (4.10) останется прежней.
По аналогии с только что рассмотренным примером формулой (4.11) можно оценивать неупорядоченность потока смеси каких-либо веществ. В этом случае 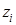 – концентрация i -го компонента в мольных долях; N – расход потока или число молекул, проходящее через некоторое сечение в единицу времени. Поскольку число N в практических задачах всегда очень велико, можно перейти к иному масштабу для энтропии. Например, поделив левую и правую части на число Авогадро, получим
– концентрация i -го компонента в мольных долях; N – расход потока или число молекул, проходящее через некоторое сечение в единицу времени. Поскольку число N в практических задачах всегда очень велико, можно перейти к иному масштабу для энтропии. Например, поделив левую и правую части на число Авогадро, получим
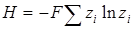 , (4.12)
, (4.12)
где F – расход потока, кмоль/ед. времени. Обозначение энтропии в новом масштабе оставлено прежним.
Таким образом, энтропия оценивает разнообразие элементов в системе по некоторому определенному признаку, который может нас интересовать в той или иной задаче; см п. 4.6 и 4.7.
Обратим внимание, что выражение (4.10) с точностью до множителя совпадает с термодинамическим выражением для мольной энтропии смешения идеального газа
DS = – R 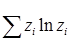 , (4.13)
, (4.13)
где R – газовая постоянная.
На этом примере можно заметить связь информационной энтропии, введенной в предыдущих разделах без использования каких-либо физических принципов, с термодинамикой. Здесь полезно также отметить не только внешнюю, структурную аналогию. Энтропия смешения (4.13) это только энтропия термодинамически и д е а л ь н о й смеси. При рассмотрении камеры с шарами также были приняты некоторые ограничения, например, требование равных размеров шаров.
Энтропию, записанную через вероятности, часто называют функциональной, в отличие от энтропии, выраженной через мольные доли, которую именуют атрибутивной.
4.5.Связь информационной энтропии с физикой. Понятие энтропии впервые было введено в термодинамику Клаузисом как соотношение, связывающее элементарное приращение энтропии dS с элементарным количеством теплоты dQ при температуре Т
dS = dQ/T (4.14)
Это выражение мало говорит о физической сущности энтропии. В физике неоднократно делались попытки раскрыть содержание этого понятия, руководствуясь модельными представлениями.
Энтропия Больцмана. Рассмотрим основанное на статистическом подходе известное уравнение Больцмана
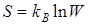 , (4.15)
, (4.15)
где kB – постоянная Больцмана, kB =1,38×10 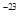 Дж/К;
Дж/К;
W – число микросостояний.
Для того чтобы понять сущность статистических методов в качестве начального примера рассмотрим газ, как ансамбль большого числа частиц. Первое, что кажется необходимо сделать при построении математической модели поведения частиц, это попытаться записать уравнение движения для каждой из них, ведь газ, во всяком случае в первом приближении, представляет собой систему частиц, движущихся по законам механики Ньютона.
Однако при таком подходе число уравнений становится невообразимо велико, не говоря уже о том, что для интегрирования этих уравнений необходимы начальные скорости и координаты каждой молекулы. Тем не менее, такой путь не только сложен, но и бесплоден, поскольку знание траекторий и закона движения отдельных молекул оказывается не даёт никакой информации относительно свойств газа в целом. Дело в том, что в системе, состоящей из многих частиц, возникают новые, чисто статистические системные, или интегративные закономерности, которых не было в системе с малым числом частиц.
Проследим на весьма упрощённой модели, как появляются эти новые свойства, связанные с понятием энтропии Больцмана.
Для наглядности возьмем систему всего из десяти частиц (N =10), распределённых на четырёх энергетических уровнях, имеющих относительные величины энергии 1, 2, 3 и 4. Общая энергия системы равна 20 относительным единицам. Задача заключается в том, чтобы высказать некоторые соображения относительно того состояния, которое примет система, предоставленная самой себе, т.е. относительно того, как распределятся частицы по уровням энергии.
Для этого выясним, какие энергетические распределения частиц возможны. При этом будем различать изменения микро- и макросостояния системы. Если произошло изменение ч и с л а частиц на каком-либо энергетическом уровне, то будем говорить об изменении макросостояния системы. Если же произошёл только о б м е н частиц между энергетическими уровнями, но число частиц на каждом уровне энергии осталось прежним, будем фиксировать изменение микросостояния системы. Для внешнего наблюдателя, следящего только за макросостояниями системы, изменения микроскопического характера окажутся незамеченными, а микросостояния неразличимы. Одно макросостояние может быть реализовано с помощью очень многих микросостояний.
Так, одно из возможных макросостояний в рассматриваемой системе из десяти частиц таково: на первом энергетическом уровне находится одна частица (N 1=1), на втором располагаются восемь частиц (N 2=8) и одна занимает третий уровень (N 3=1). Четвертый уровень не занят. Общая энергия равна 1×1+8×2+1×3+ 4×0=20. Предположим, что частицы пронумерованы. Тогда данное макросостояние можно было бы осуществлять различным способом (через различные микросостояния), помещая, например, на уровень c энергией 1 поочерёдно частицы с номером 1, 2, 3, 4, 5 и т.д., т.е. осуществляя разные перестановки частиц, не нарушая макросостояния системы.
Число возможных перестановок можно рассчитать по следующей формуле статистической физики:
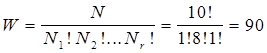 . (4.16)
. (4.16)
Здесь r – число энергетических уровней; в данном примере r = 4.
Если теперь перейти к другому макросостоянию, т.е. взять иное распределение частиц по энергетическим уровням, например, N 1=2, N 2=7, N 3=0 и N4=1 (общая энергия 2×1+7×2+1×4 = 20), то число способов осуществления данного макросостояния W оказывается равным 360.
Сводные результаты расчёта для всех возможных макросостояний приведены в табл.4.1, из которой следует, что для данной системы из 10 частиц возможны 14 макросостояний и 44803 различных микросостояния. Важно отметить, что из всех микросостояний около 28% принадлежит только одному макросостоянию (последняя строка в таблице).
Следовательно, если вероятность пребывания системы в любом микросостоянии одинакова и равна 1/44803, то вероятность пребывания системы в том или ином макросостоянии оказывается различной и тем значительней, чем больше способов осуществления данного макросостояния.
В данном примере в среднем в 28 из 100 случаев система, предоставленная самой себе, будет принимать макросостояние, соответствующее последней строке таблицы. В примере участвует только 10 частиц и всего лишь 4 энергетических уровня. Анализ показывает, что если число частиц и число энергетических уровней станет очень большим, как это имеет место в реальных системах, то всегда есть одно макросостояние, число способов осуществления которого (число микросостояний) будет значительно преобладать над остальными. Например, более 99,99% всех возможных микросостояний может принадлежать только одному макросостоянию. Это конкретное макросостояние, которое осуществляется максимальным числом способов, определяет свойства системы, и является наиболее вероятным, поэтому всеми другими распределениями можно пренебречь. Далее под числом W будем понимать число способов осуществления только одного, наиболее вероятного макросостояния. При этом оказывается, что энтропия Больцмана (4.15) с точностью до постоянного множителя совпадает с величиной ln W.
Согласно второму началу термодинамики энтропия неравновесной закрытой системы может только повышаться, что означает по Больцману увеличение числа возможных микросостояний.
Табл. 4.1
Распределение частиц по энергетическим уровням.
| Номер | Уровни энергии | Wj | Wj/SWj ×100 | |||
| J | ||||||
| 0,2 | ||||||
| 0,6 | ||||||
| 0,8 | ||||||
| 1,9 | ||||||
| 2,8 | ||||||
| 2.8 | ||||||
| 7,0 | ||||||
| 7.0 | ||||||
| 9,4 | ||||||
| Всего |
Если теперь воспользоваться информационной энтропией для оценки неопределённости, связанной с установлением (определением) того микросостояния, в котором находится система в данный момент, то, принимая во внимание, что все микросостояния равновероятны, получаем согласно формуле (4.4):
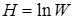 . (4.17)
. (4.17)
Сравнивая выражения (4.15) и (4.17), нельзя не обнаружить их сходство. Они отличаются лишь на величину постоянного множителя, что для информационной энтропии не имеет принципиального значения. Заметим, что размерность физической энтропии Дж/К в известной мере условна, так как связана исключительно с использованием температурной шкалы для оценки степени нагретости тела. Если для этой же цели использовать энергетическую шкалу, как это часто принимается в физике, т.е. под температурой подразумевать произведение kBТ, тогда и физическая энтропия станет безразмерной. По глубокому физическому смыслу энтропия безразмерна.
Покажем, что аналогия между энтропией Больцмана и информационной энтропией существует не только для равновероятных событий (формула (4.4), но и для общего случая (4.7). Раскроем значение W, воспользовавшись выражением (4.16), предварительно прологарифмировав его:
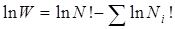 .
.
Используя формулу Стирлинга 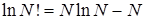 , находим
, находим 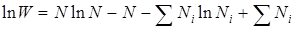 . Заметив, что
. Заметив, что 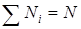 , а
, а 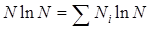 , получаем:
, получаем:
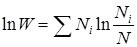 .
.
Умножив обе части этого выражения на 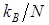 и полагая, что
и полагая, что 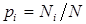 есть вероятность обнаружить частицу на i -м энергетическом уровне, имеем:
есть вероятность обнаружить частицу на i -м энергетическом уровне, имеем:
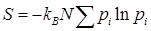 .
.
Таким образом, получили выражение, аналогичное информационной энтропии (4.7).
Когда речь идёт о физической энтропии, то всегда имеют в виду неупорядоченность только одного рода, а именно неупорядоченность, связанную с хаотическим тепловым движением молекул. При этом способ оценки неупорядоченности (через логарифм вероятности) в термодинамике и теории информации остаётся одним и тем же.
Поскольку понятие энтропии в теории информации не связывается с каким-либо определённым типом неупорядоченности, то в этом смысле оно является более широким, чем понятие энтропии в статистической физике.
Термодинамическая энтропия. Уравнение Больцмана формулирует энтропию модельными средствами на вероятностной основе независимо от феноменологии термодинамики. Исторически это было связано с попыткой увязать некоторые термодинамические параметры с механикой, отчасти также с тем, что классическая термодинамика, в которой энтропия введена соотношением Клаузиуса (4.14), не дает детального описания явления, связанного с этим фундаментальным термодинамическим параметром. Не в последнюю очередь это связано с тем, что природа термодинамической энтропии дискретна, а ее истолкование в физике происходит на классической, непрерывной (континуальной) основе.
Рассмотрим новые возможности, которые предоставляет обобщенная, нелокальная версия термодинамики с дискретной энтропией в раскрытии физического содержания термодинамической энтропии.
Убедимся, прежде всего, что при подстановке в соотношение Клаузиуса макроквантовых аналогов для минимальных приращений энтропии и теплоты dS® kB и dQ® kBT, выражение (4.14) переходит в обычное тождество kB=kB.
Это тождество, преобразованное вместе с другими термодинамическими параметрами в предельно разностную дискретную форму, позволяет получить в рамках НВТ иные тождества, проясняющие физический смысл энтропии.
Так для энтропии макроячейки было найдено [7,c.26]
Sm =kB T/ D T S =kB ( mch2/m v2), (4.17)
где ch= (SmT/m)1/2 – скорость тепловых фононов; v =(kT/m)1/2 – когерентная (коллективная) составляющая скорости частиц макроячейки; m – масса макроячейки; D TS – квантовый разброс температуры при постоянной энтропии.
Z=T/ D TS =mch2/mv2
Как следует из приведенных соотношений квантовый разброс температуры D TS, а также скорость тепловых фононов определяется через энтропию. Это означает, что выражение (4.4) не претендует на вычисление энтропии, а лишь подтверждает свое происхождение из исходного тождества Клаузиуса. Ценность записи (4.4) заключается в возможности очень простой трактовки физического смысла энтропии: термодинамическая энтропия макроячейки Sm пропорциональна отношению тепловой (неупорядоченной) энергии к механической (упорядоченной) энергии частиц в макроячейке. Коэффициентом пропорциональности выступает постоянная Больцмана kB.
Теперь вновь воспользуемся свойством исходного тождества Клаузиуса и попытаемся придать ему структуру уравнения Больцмана. Чтобы выражение (4.4) обращалось в тождество с сохранением структуры соотношения Больцмана, следует ввести число возможных «микросостояний» W =2 Z, возникающих в макроячейке из Z =Sm/kB квантовых уровней, как число возможных сочетаний из Z элементов c двумя их разновидностями.
Тогда формально энтропии макроячейки можно придать форму уравнения Больцмана
Sm = kBZ = kB log2 W (4.18)
В справедливости этого выражения сомневаться не приходится, поскольку это всего лишь другая форма исходного тождества Клаузиуса.
По форме это выражение отличается от уравнения Больцмана (4.15) только двоичным основанием логарифма, что сближает термодинамическую энтропию с информационной. Происхождение двоичных логарифмов связано с дискретностью термодинамической энтропии в НВТ.
Однако физическое содержание числа микросостояний W в сравниваемых формулах различно. В уравнении Больцмана по энергетическим уровням распределялись ч а с т и -ц ы, в термодинамическом варианте распределяются уровни только двух типов: «возмущен», «невозмущен».
Например, на рис.4.2 изображены 8 возможных микросостояний макроячейки с тремя энергетическими уровнями (относительная энтропия Sm/kB =3). Тонкими линиями обозначены невозбужденные, а жирными – возбужденные энергетические уровни.
Для энтропии Больцмана имеет принципиальное значение указание: к а к и е частицы размещены на том или ином энергетическом уровне. Для одинакового сорта частиц это требование противоречит принципу тождественности частиц, поскольку взаимный обмен равным числом тождественных частиц между двумя уровнями энергии с точки зрения термодинамики не должен приводить к новому микросостоянию.
                      
| |||||||
  
|
Date: 2015-05-22; view: 441; Нарушение авторских прав