
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства операции транспонирования матриц
|
|
1. 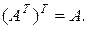
2. 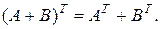
3. 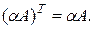
Доказательство свойств 1−3 осуществляется прямыми вычислениями (самостоятельно).
4. 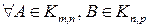 справедливо
справедливо 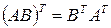
Доказательство: 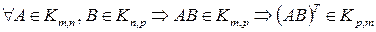
Легко видеть, что 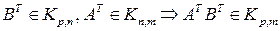 .
.
Пусть 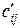 – элемент матрицы
– элемент матрицы 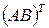 ,стоящий в
,стоящий в 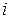 –й строке и
–й строке и 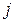 –том столбце
–том столбце 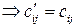 ,где
,где 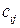 – элемент
– элемент 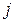 –ой строки и
–ой строки и 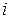 –того столбца матрицы
–того столбца матрицы 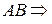
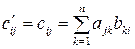 , где
, где 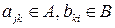
Но 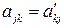 ,
, 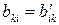 , где
, где 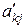 и
и 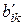 – элементы
– элементы 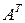 и
и 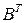 , соответственно =>
, соответственно => 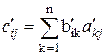 , где последняя сумма – произведение элементов
, где последняя сумма – произведение элементов 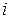 –ой строки
–ой строки 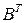 на
на 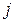 –ой столбец
–ой столбец 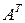 ,те
,те 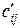 – элемент
– элемент 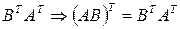 (что и требовалсоь доказать).
(что и требовалсоь доказать).
5. 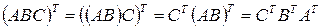

Определение 4. Если квадратная 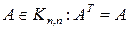 , то
, то  называется симметричной, тогда
называется симметричной, тогда 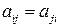 , если
, если 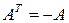 т.е.
т.е. 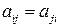 , то
, то  – называется кососимметричной (антисимметричной).
– называется кососимметричной (антисимметричной).
Свойство 1. Определитель транспонированной матрицы равен определителю исходной матрицы, т.е. 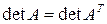
Доказательство: Пусть 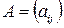 ,
, 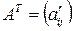 , т.к.
, т.к. 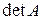 и
и  имеют одинаковое количество членов
имеют одинаковое количество членов 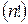 , то достаточно показать, что
, то достаточно показать, что  член
член 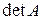 является членом
является членом  и наоборот.
и наоборот.
Все члены 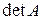 имеют вид:
имеют вид:  и составлены из членов, находящихся в разных строках и столбцах
и составлены из членов, находящихся в разных строках и столбцах 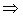 этот же член является членом
этот же член является членом  . Верно и обратное
. Верно и обратное 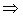 члены определителя одни и те же, осталось разобраться со знаками.
члены определителя одни и те же, осталось разобраться со знаками.
Знак  равен
равен 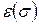 . Этот член входит в
. Этот член входит в  как
как 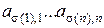 и имеет знак
и имеет знак 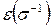 (см. свойство 2 перестановок)
(см. свойство 2 перестановок) 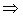 т.к.
т.к. 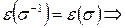 определители
определители  и
и 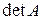 являются суммами одинаковых членов с одинаковыми знаками
являются суммами одинаковых членов с одинаковыми знаками 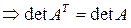 (что и требовалось доказать).
(что и требовалось доказать).
Следствие: Всякая теорема об определителе остается справедливой, если слово строка заменить на слово столбец и наоборот.
Свойство 2. Если одна из строк определителя состоит из 0,то определитель равен нулю.
Доказательство: На самом деле, пусть 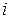 –я строка нулевая,тк в каждый член определителя входит один её элемент
–я строка нулевая,тк в каждый член определителя входит один её элемент 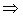 все члены нулевые
все члены нулевые 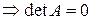 (что и требовалось доказать).
(что и требовалось доказать).
Свойство 3. Если матрица 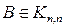 получена из
получена из 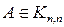 перестановкой каких–либо двух строк, то
перестановкой каких–либо двух строк, то 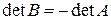
Доказательство: Пусть 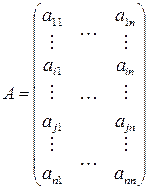 ,
, 
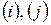 –строки
–строки
Если  входит в
входит в  , то все его члены и в
, то все его члены и в 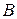 остаются в разных столбцах и строках
остаются в разных столбцах и строках 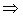 он входит и в
он входит и в 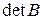 . Для
. Для  знак
знак 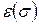 , а в
, а в 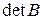 надо считать знак перестановки
надо считать знак перестановки 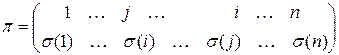 эта перестановка получается из
эта перестановка получается из 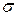 транспозицией в верхней строке
транспозицией в верхней строке 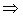 она имеет противоположную четность, т.е.
она имеет противоположную четность, т.е. 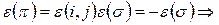 все члены
все члены 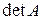 входят в
входят в 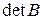 с противоположным знаком
с противоположным знаком 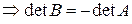 (что и требовалось доказать).
(что и требовалось доказать).
Свойство 4. Определитель,содержащий две одинаковые строки,равен нулю
Доказательство: Пусть в  и
и 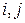 –строки равны
–строки равны 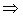 после их перестановки определитель равен
после их перестановки определитель равен 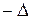 , но т.к. переставлены одинаковые строки
, но т.к. переставлены одинаковые строки 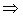 он тот же самый
он тот же самый 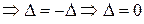 .
.
Свойство 5. Если 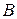 получена из
получена из  умножением некоторой строки на
умножением некоторой строки на 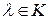 , то
, то 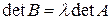 .
.
Доказательство: 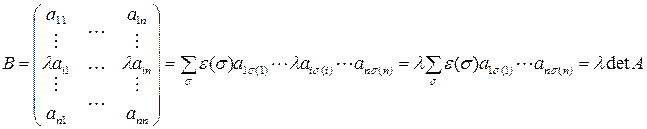
Свойство 6. Если  содержит две пропорциональные строки, то
содержит две пропорциональные строки, то 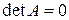 .
.
Доказательство: Пусть 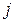 –я строка равна
–я строка равна 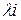 –строка
–строка 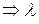 можно вынести из
можно вынести из 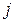 –й строки (свойство 5)
–й строки (свойство 5) 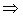 по свойству 4
по свойству 4 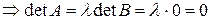 (что и требовалось доказать).
(что и требовалось доказать).
Свойство 7. Если все элементы 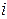 –ой строки матрицы
–ой строки матрицы 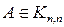 представлены в виде двух слагаемых:
представлены в виде двух слагаемых:  , то
, то 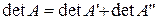 , где
, где 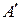 ,
, 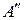 имеют все строки, кроме
имеют все строки, кроме 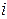 –ой, как в
–ой, как в  , а
, а 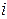 –ая строка
–ая строка 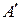 состоит из
состоит из 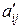 , а
, а 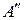 – из
– из 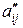 , т.е.
, т.е.
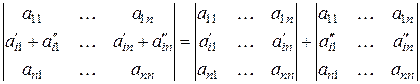
Доказательство:
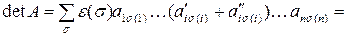
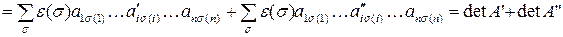 (что и требовалось доказать).
(что и требовалось доказать).
Следствие: Тоже самое, когда 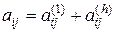 , т.е. сумма
, т.е. сумма 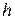 слагаемых.
слагаемых.
Свойство 8. Если одна из строк определители есть линейная комбинация его других строк, то определитель равен нулю.
Доказательство: Если 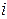 –ая строка, есть линейная комбинация остальных
–ая строка, есть линейная комбинация остальных 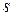 строк
строк 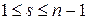 , то
, то  элемент
элемент 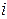 –ой строки – сумма
–ой строки – сумма 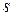 элементов
элементов 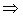 по следствию к свойству 7 определитель можно представить как сумму определителей, в каждом из которых
по следствию к свойству 7 определитель можно представить как сумму определителей, в каждом из которых 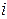 –ая строка пропорциональна одной из строк
–ая строка пропорциональна одной из строк 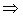 они равны
они равны 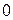 (что и требовалось доказать).
(что и требовалось доказать).
Свойство 9. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и тоже число.
Доказательство: Если к 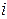 –ой строке прибавляется
–ой строке прибавляется 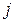 –ая строка, умноженная на
–ая строка, умноженная на 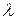 , то в новом определители
, то в новом определители 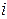 –ая строка равна
–ая строка равна 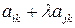 . Тогда на основании 7 этот определитель – это сумма двух определителей, один из которых равен
. Тогда на основании 7 этот определитель – это сумма двух определителей, один из которых равен 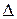 , а второй содержит две пропорциональные строки
, а второй содержит две пропорциональные строки 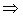 равен
равен 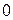 (что и требовалось доказать).
(что и требовалось доказать).
Следствие: Определитель не менятся,если к одной его строке добавляется линейная комбинация других строк.
30.Миноры и алгебраические дополнения.
Пусть 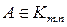 . Выберем
. Выберем  номеров строк
номеров строк  и
и  номеров столбцов
номеров столбцов 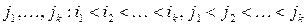 .
.
Определение 5. Минором порядка  матрицы
матрицы  называется определитель матрицы порядка
называется определитель матрицы порядка  , образованной элементами, находящимися на пересечении выбранных строк и столбцов.
, образованной элементами, находящимися на пересечении выбранных строк и столбцов.
Обозначение: 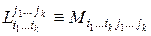
Примеры: 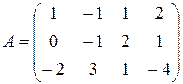 ,
, 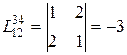 ,
, 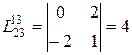
Определени 6. Если  – квадратная порядка
– квадратная порядка 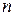 , то каждому минору
, то каждому минору 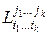 порядка
порядка  можно поставить в соответствие дополнительный минор
можно поставить в соответствие дополнительный минор 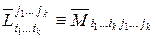 порядка
порядка 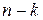 , элементы которого расположены на пересечении остальных строк и столбцов. Очевидно, что минор
, элементы которого расположены на пересечении остальных строк и столбцов. Очевидно, что минор 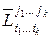 будет в свою очередь дополнительным к
будет в свою очередь дополнительным к 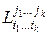 .
.
Алгебраическими дополнениями минора 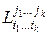 называется произведение дополнительного минора на
называется произведение дополнительного минора на 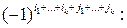
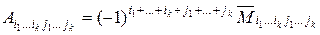
Если 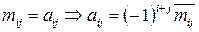 .
.
Пример: 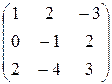
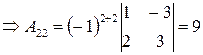
Теорема 1 (о разложении определителя).
Если 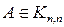 и
и  , то
, то 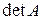 равен сумме произведений элементов любой строки матрицы
равен сумме произведений элементов любой строки матрицы  на их алгебраические дополнения, т.е.
на их алгебраические дополнения, т.е. 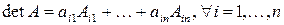 .
.
Доказательство: Пусть
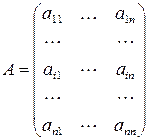 . Тогда, выбрав
. Тогда, выбрав 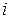 –ую строку, определитель
–ую строку, определитель  можно представить как сумму:
можно представить как сумму:
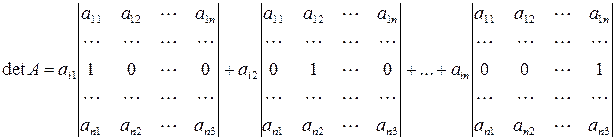 , где
, где 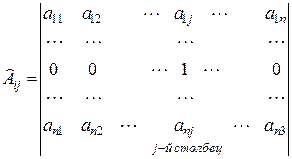 i-я строка
i-я строка
Покажем, что 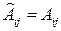 . Переставляя
. Переставляя 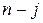 раз столбцы и
раз столбцы и 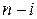 раз строки, получим:
раз строки, получим: 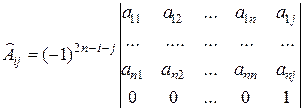
Лемма 1: 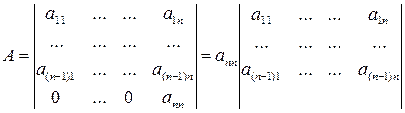
Доказательство: 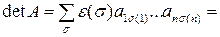
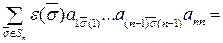

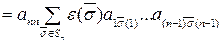 .
.
Рассмотрим 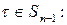
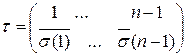 . Очевидно, что
. Очевидно, что 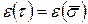 так что число инверсий в
так что число инверсий в 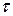 и
и 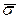 одно и тоже и значит
одно и тоже и значит 
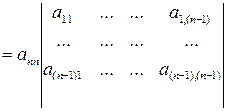 (что и требовалось доказать).
(что и требовалось доказать).

 Вернемся к доказательству теоремы:
Вернемся к доказательству теоремы: 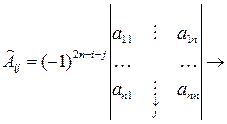
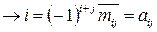 (что и требовалось доказать).
(что и требовалось доказать).
Следствие (разложение по чужой строке).
Сумма произведений всех элементов какой–нибудь строки определителя на алгебраические дополнения соответствующих элементов другой строки равна нулю.
Доказательство: Пусть 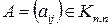 . Рассмотрим матрицу
. Рассмотрим матрицу 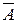 , получающуюся из
, получающуюся из  заменой
заменой 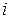 –ой строки на
–ой строки на 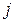 –ю, оставляя
–ю, оставляя 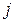 –ю прежней
–ю прежней 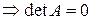 . Напишем разложение
. Напишем разложение 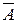 по
по 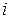 –ой строке:
–ой строке: 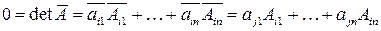 т.к. алгебраические дополнения к элементам
т.к. алгебраические дополнения к элементам 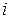 –ой строки у матрицы
–ой строки у матрицы  и
и 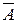 совпадают (что и требовалось доказать).
совпадают (что и требовалось доказать).
Пример:
1) 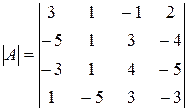
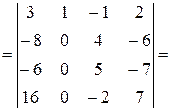
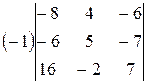 =
= 
Следующая теорема обобщает теорему 1.
Теорема 2 (теорема Лапласа).
Пусть матрице  порядка
порядка 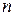 произвольно выбраны
произвольно выбраны  строк,
строк, 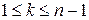 . Тогда сумма произведений всех миноров
. Тогда сумма произведений всех миноров  –го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна
–го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна 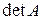 . Т.е. если
. Т.е. если  – выбранные строки, то
– выбранные строки, то 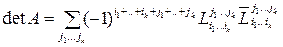 (1),
(1),
где суммирование ведется по всевозможным значениям индексов 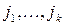 ,
, 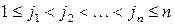 .
.
Формула (1) называется формулой разложения определителя по  –й строке
–й строке  .
.
Доказательство: см. Ильин, Поздяк стр. 27.
Примеры:
1)
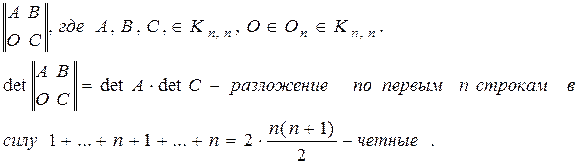
2)
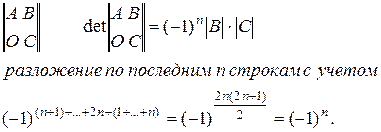
3) Определитель Вандермонда.

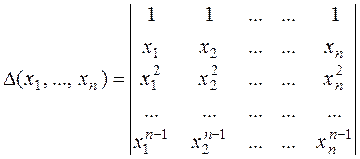
Вычитая первый столбец из всех остальных, получаем:
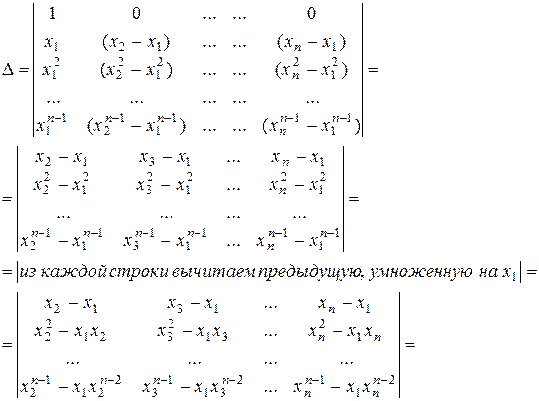

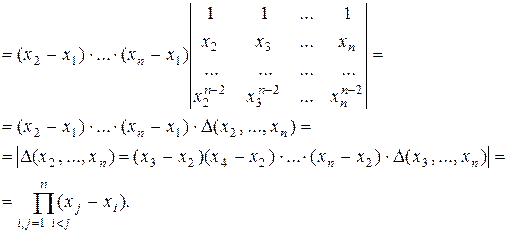
4°. Определитель суммы и произведения матриц.
Непосредственно из линейного свойства определителя вытекает:
Теорема 1: Если 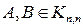 , то
, то 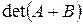 равен сумме определителей матриц порядка
равен сумме определителей матриц порядка 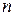 , каждая из которой получается следующим образом: часть строк (столбцов) берутся совпадающими с соответствующими строками (столбцами) матрицы
, каждая из которой получается следующим образом: часть строк (столбцов) берутся совпадающими с соответствующими строками (столбцами) матрицы  , а остальные – совпадающие с соответствующими строками (столбцами) матрицы B.
, а остальные – совпадающие с соответствующими строками (столбцами) матрицы B.
Иллюстрация 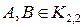 .
.
Теорема 2: Если 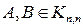 , то
, то 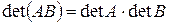 .
.
Доказательство: Рассмотрим матрицу 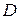 порядка
порядка 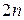 :
: 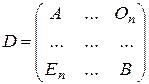 , где
, где  – нулевая квадратная матрица порядка
– нулевая квадратная матрица порядка 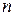 ,
,

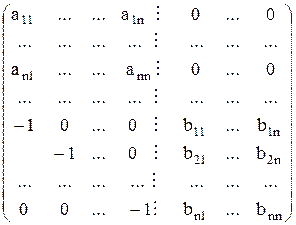
Из примера 1 пункта 3 имеем, что 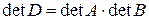 .
.
Преобразуем теперь матрицу 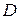 .
. 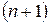 строку умножим на
строку умножим на 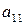 ,
, 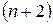 – на
– на 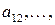
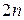 –ую – на
–ую – на 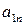 и сложим с первой строкой. Тогда первая строка имеет вид:
и сложим с первой строкой. Тогда первая строка имеет вид: 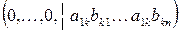 . Аналогично к
. Аналогично к 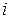 –ой строке прибавим
–ой строке прибавим 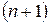 , умноженную на
, умноженную на 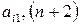 – на
– на 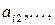
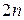 –ую на
–ую на  .
.
Имеем: 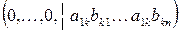 . Т.о., первые
. Т.о., первые 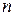 строк принимают вид:
строк принимают вид:
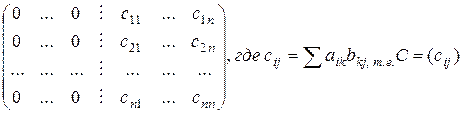
При таких преобразованиях определитель не меняется 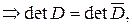
где 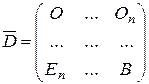 . Но
. Но 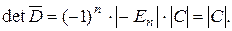 Т.о. доказано, что
Т.о. доказано, что
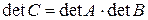 det.
det.
Следствие 1: Если 
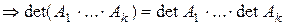
Следствие 2: Из 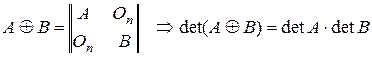
5°. Обратная матрица. Пусть  – квадратная матрица порядка
– квадратная матрица порядка 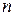 над полем
над полем 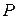 .
.
Определение 1. Матрица 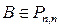 называется обратной для
называется обратной для  , если
, если 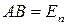 .
.
Определение 2. Квадратная матрица  называется невырожденной (или неособой), если
называется невырожденной (или неособой), если 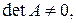 и вырожденной (особой), если
и вырожденной (особой), если 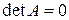 .
.
Из теоремы 2 пункта 4 Þ произведение матриц, одна из которых вырождена, будет вырожденной матрицей, а произведение двух невырожденных матриц дает невырожденную матрицу.
Определение 3. Матрицей присоединенной к матрице  , называется матрица
, называется матрица
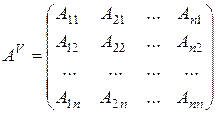 ,
,
где  – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 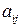 матрицы
матрицы  .
.
Лемма: Для матриц  и
и 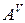 справедливо
справедливо 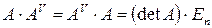 .
.
Доказательство: Пусть 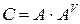 . Тогда
. Тогда

Итак, 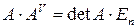 . Аналогично
. Аналогично 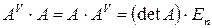 .
.
Теорема 1: Для того, чтобы для матрица  существовала обратная, необходимо и достаточно, чтобы матрица
существовала обратная, необходимо и достаточно, чтобы матрица  была невырожденной.
была невырожденной.
Доказательство: Þ Пусть для матрицы 

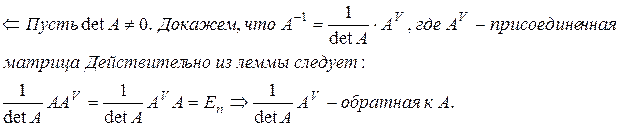
Замечание: итак 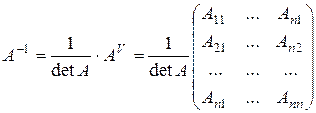
Пример:
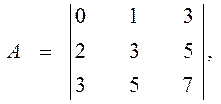

Свойства обратных матриц:
Пусть 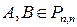
Тогда
1. 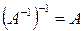
2. 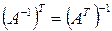
3. 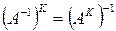
4. 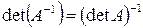
5. 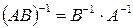
Date: 2015-04-23; view: 1197; Нарушение авторских прав