Плоско-параллельное движение

Плоско-параллельное движение (ППД) представляет собой вращение без указания осей. На рис. 107 показано применение ППД для определения натуральной величины треугольника АВС.

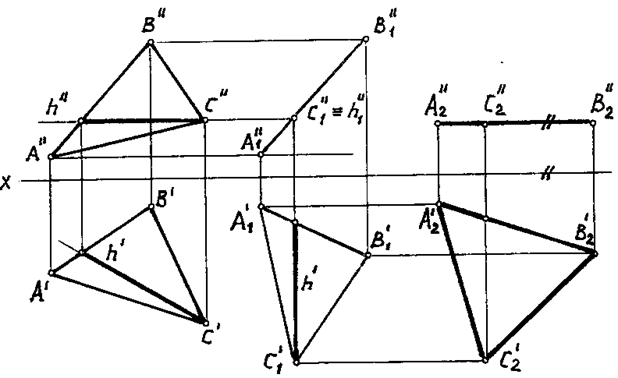
Рис. 107

ПЕРВЫМ ПОВОРОТОМ треугольник приведен в положение А ₁ В ₁ С ₁, перпендикулярное к плоскости H. Построение выполнено с помощью фронтали А ₁, которая вращением вокруг оси, перпендикулярной к плоскости V, расположена перпендикулярно к горизонтальной плоскости проекций H (рис. 107).

Так как фронтальные проекции проецируемого объекта, вращаемого вокруг оси, перпендикулярной к плоскости проекций V, не изменяют ни своей формы, ни величины, фронтальная проекция А"В"С" отнесена параллельно самой себе на свободное место чертежа (рис. 107).

Горизонтальная проекция А'B'C ' получена путем проведения линий связи от фронтальной проекции А"В"С" и переноса глубины (координата y) каждой вершины треугольника.

ВТОРЫМ ПОВОРОТОМ вокруг оси, перпендикулярной к плоскости H, А ₁ В ₁ С ₁ приведен в положение А ₂ В ₂ С ₂, параллельное фронтальной плоскости V, при котором горизонтальная проекция А'B'C ' будет параллельна оси x.

Эта проекция отнесена на чертеже (рис. 107) вправо путем параллельного перемещения на удобное место. Проведя через точки А" ₂ В" ₂ С" ₂ линии связи (перпендикулярно оси x) и перенося высоты (координаты z) точек А, В, С, находим точки А '₂ В '₂ С '₂ Соединяя эти точки последовательно прямыми, получим треугольник А””є, являющийся натуральной величиной треугольника АВС (рис. 107).

9. ЛИНИИ И ПОВЕРХНОСТИ

План:

9.1. ЛИНИЯ

Винтовая линия

9.2. ПОВЕРХНОСТЬ

Поверхности линейчатые

Поверхности линейчатые развертывающиеся

Поверхности линейчатые неразвертывающиеся

Поверхности нелинейчатые

Поверхности параллельного переноса, вращения

Поверхности вращения

Поверхности винтовые

ЛИНИЯ

ЛИНИЯ — это множество всех последовательных положений движущейся точки.

Евклид: “Линия же — длина без ширины”.

Прямая — разновидность линии, которая получается, если движущаяся точка не изменяет направления движения.

Кривая — разновидность линии, которая получается, если движущаяся точка изменяет направление движения.

Плоские линии — линии, все точки которых принадлежат одной плоскости.

Пространственные линии (линии двоякой кривизны) — линии, все точки которых не принадлежат одной плоскости (например, линии пересечения поверхностей).

Алгебраические линии определяются алгебраическими уравнениями в декартовой системе координат (окружность, эллипс, парабола, гипербола и др.).

Трансцендентные линии описываются трансцендентными уравнениями (синусоида, спираль Архимеда и др.).

Если алгебраическое уравнение линии n ‑й степени, то алгебраическая кривая считается n ‑го порядка, то есть ПОРЯДКОМ КРИВОЙ называют наибольшую степень ее уравнения.

Геометрически порядок плоской кривой определяется наибольшим числом точек ее пересечения с прямой, лежащей в плоскости кривой, а для пространственной кривой — пересечением ее с плоскостью.

Для алгебраических кривых это число точек всегда конечно. Для трансцендентных — бесконечно. Например, для эллипса (рис. 108)

x ²/ a ² + y ²/ b ² = 1

имеем n = 2, т.е. это — кривая второго порядка.

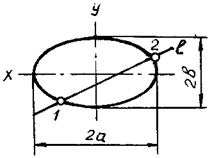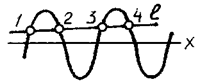Рис. 108 Рис. 109

Для синусоиды (рис. 109) y = sin x имеем n = ¥.

Кривые бывают закономерные и незакономерные, как, например, горизонтали на географической карте.

Винтовая линия

Пространственная кривая, широко применяемая в технике.

Цилиндрическая винтовая линия — пространственная кривая, получающаяся в результате двойного равномерного движения точки: вращения вокруг оси и поступательного движения вдоль прямой, параллельной этой оси (рис. 110).

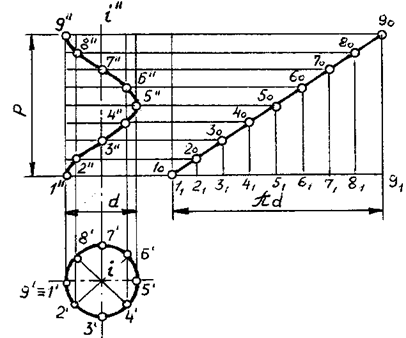
Рис. 110

p — шаг винтовой линии или расстояние между двумя ее соседними витками в направлении, параллельном оси i. Шаг определяет величину перемещения точки в направлении оси за один оборот этой точки вокруг оси.

Проекция цилиндрической винтовой линии на горизонтальную плоскость проекций (при i ^ H) — окружность, на фронтальную плоскость проекций — синусоида.

Отрезок [1_o1_o1] — развертка цилиндрической винтовой линии.

j^o — угол подъема винтовой линии.

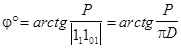
Цилиндрические винтовые линии бывают правые и левые. Основание для такого деления — направление движения точки, спускающейся по винтовой линии. Если проекция этого направления на плоскость, перпендикулярную к оси винтовой линии, совпадает с направлением движения часовой стрелки — винтовая линия ПРАВАЯ. В противном случае — ЛЕВАЯ.

Коническая винтовая линия — пространственная кривая, получающаяся в результате двойного равномерного движения точки: вращения вокруг оси и поступательного движения вдоль прямой, пересекающейся с этой осью (рис. 111).

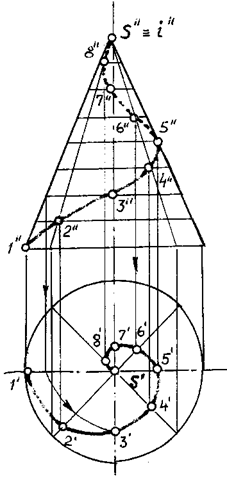
Рис. 111

При i ^ H горизонтальная проекция конической винтовой линии — архимедова спираль, фронтальная — затухающая синусоида.

Date: 2015-04-23; view: 683; Нарушение авторских прав