Д /уі g(x) [a,b] өспейтін болсын

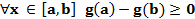
(G(x)-g(b) ф-сы [a,b] де теріс емес өспейтін және [a,b] да интегралданады.

Оған 2ши Лемманы қолдансақ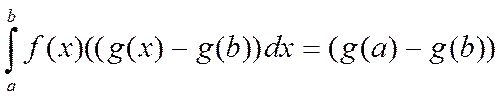

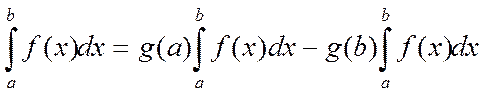
7. Бірінші және екінші текті меншіксіз интегралдар. Меншіксіз интегралдардың жинақтылығының жеткілікті шарттары.

1. Бірінші жəне екінші текті меншіксіз интегралдар

I. а) f функциясы [a,+∞) аралығында берілсін;

б) f - кез келген ақырлы [a b ′], кесіндісінде мұндағы, b ′ ∈ (a +∞) интегралданатын болсын. Eгер 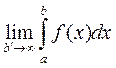болса, онда ол шек f(x) функциясының [a, ∞] аралығындағы (бірінші текті) меншіксіз интегралы деп аталады да келесі түрде белгіленеді

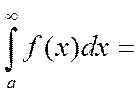
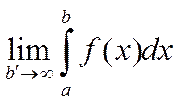(1)

II. а) f шекті [a,b) аралығында берілген жəне b- нүктесінің маңайында шектелмеген функция;

б) f кез келген [a, b ′] кесіндісінде (a < b ′ < b интегралданатын функция болсын. Егер 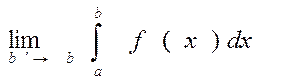(2) шегі болса, онда ол шек f функциясының [ a,b] кесіндісіндегі (екінші текті)

меншіксіз интегралы деп атайды да оны

деп жазылады. (1) жəне (2) интегралдарды жинақты деп атайды.

Егер f функциясы үшін І немесе ІІ шарттың тек бірі ғана орындалса, онда

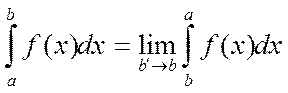деп жазылады да (1) және (2) интегралдары жинақты деп атайды.f(x) функциясы ақырсыз 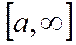аралығында анықталған және кез келген ақырлы 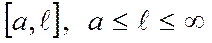кесіндісінде интегралданатын функция дейік. Егер 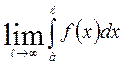шегі бар болса, онда ол шек 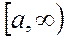аралығында f(x) функциясының меншіксіз интегралы деп аталады.да 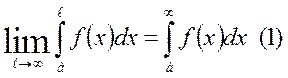арқылы белгіленеді. Егер шек ақырлы болса, онда меншіксіз интеграл жинақталады дейді. Егер де бұл шек ақырсыз болса, немесе тіпті болмаса, онда интеграл жинақталмайтын меншіксіз интеграл деп аталады. Дәл осы сияқты 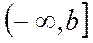жарты интервалда және 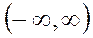интервалда меншіксіз интегралды анықтауға болады, яғни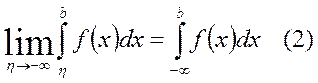 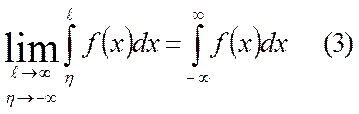. Айталық F(x) берілген f(x) функциясының алғашқы функциясы болсын. Онда Ньютон-Лейбниц формуласы бойынша интегралдардың есептеу формулаларын келтіруге болады: ,

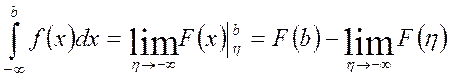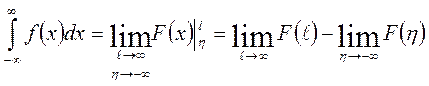
Мысалдар: 1) 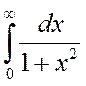меншіксіз интегралын жинақтылыққа зертелік.

Шешуі. Бірінші текті меншіксіз интегралды есептеудің (1) формуласы бойынша: 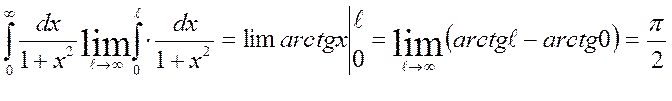Берілген меншіксіз интеграл –жинақты.

8.Көп айнымалыдан тәуелді функция. Көп айнымалыдан тәуелді функцияның шегі. Көп айнымалыдан тәуелді функция үшін Тейлор формуласы.

Бір айнымалысы бар функция табиғаттағы барлық құбылыстарды сипаттай алмайды, сондықтан көп айнымалысы бар функция ұғымы енгізіледі.

Анықтама: Егер екі тәуелсіз х,у айнымалыға бір ереже бойынша сәйкес z айнымалысы қойылса, онда айнымалы z тәуелсіз екі айнымалының функциясы деп аталады. Осы жағдайды былай жазады:

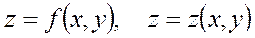т.б.т.

Мысалдар: 1 Тіктөртбұрыштың ауданы 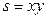формула арқылы анықталады, мұнда х-табаны, у-биіктігі.

2. Дененің көлемі үш айнымалыдан тәуелді болады: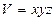

Тәуелсіз айнымалардың жиынын көп айнымалы функцияның анықтау облысы деп аталады.

Мысал: Айталық 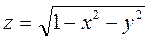екі айнымалыдан тәуелді функция берілсін. теңсіздікті қанағаттандыратын жиын осы функцияның анықтау облысы болады.

Енді екі айнымалысы бар функцияның геометриялиялық мағынасына тоқтайық. Бір айнымалысы бар функцияның геометриялық кескіні қисық сызық болатыны белгілі.

Жазықтықтың G облысында анықталған бір мәнді 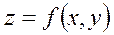функцияны қарайық. Бұл функцияға геометриялық мағына беру үшін кеңістіктегі тік бұрышты декарттық координаталардың OXYZ жүйесін қарауға тура келеді.

G облысы хоу жазықтығында жатсын. Осы G облысынан бір тиянақты (х,у) нүктені алсақ, онда бұл нүктеге кеңістіктегі, апликатасы 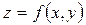болатын нүкте сәйкес келеді. Егер осы облыстың кез келген нүктесінің апликатасын анықтасақ, онда кеңістікте бір геометриялық бейне кескіндейді. Әрине бұл геометриялық бейне бет болып табылады. Сонымен, екі айнымалының функциясының геометриялық кескіні бет болып табылады. 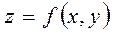теңдеуді кеңістіктегі беттің теңдеуі дейді.

Мәселен, функция 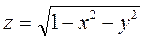ортасы координат бас нүктесінде жатқан, радиусы бірге тең сфераны кескіндейді.

ХОУ жазықтығында жатқан G облысында анықталған 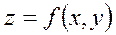функцияны қарайық. 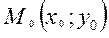осы облысының бір тиянақты нүктесі және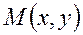

кез келген нүктесі болсын.

1-ші анықтама. Егер теңсіздігі орындалғанда, мына 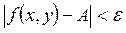теңсіздігі орындалса, онда А санын айнымалы х, х₀-ге, айнымалы у, у₀-ге ұмтылғанда 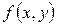функцияның шегі деп атайды.

Мұнда 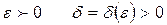құнарсыз сандар.

Функцияның шегін былай белгілейді.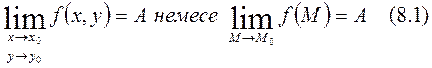

Көп айнымалыдан тәуелді функция үшін Тейлор формуласы.

Теорема 5 Егер 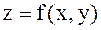және оның 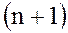-ге дейінгі барлық үзіліссіз туындылары 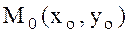нүктесінің маңайында бар және үзіліссіз болса, онда бұл функцияның осы нүктенің маңайындағы Тейлор қатары былай жазылады:

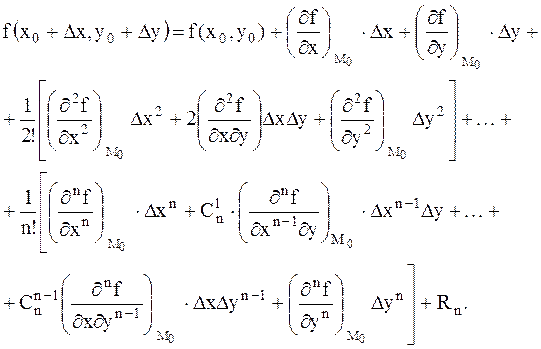(7.13)

Мұндағы Тейлор қатарының қалдық мүшесі

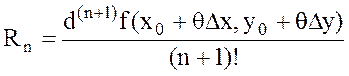
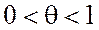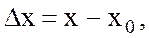
және , 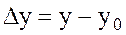деп алынған. Бұл формуланы 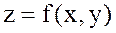функциясының Тейлор көпмүшелігі деп атайды.

9.Көп айнымалыдан тәуелді функцияның локалды экстремумы. Локалды экстремумның қажетті және жеткілікті шарттары. Шартты экстремум.

Жазықтықтың Q аймағында анықталған үзліссіз 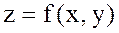функцияны қарастырайық, 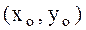осы аймақтың белгіленген ішкі нүктесі болсын.

Анықтама Егер 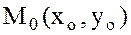нүктесінің 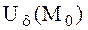маңайында жатқан барлық нүктелер үшін 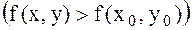немесе 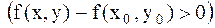теңсіздігі орындалса, онда 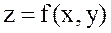функциясының 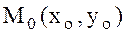нүктесінде максимумы (минимумы) бар деп айтады.

Көп айнымалды функцияның минимумы мен максимумын осы функцияның экстремумдары деп атайды.

Теорема (функцияның экстремумы болуының қажетті шарты) 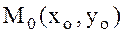нүктесінде 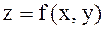функциясының экстремумы бар болу үшін, оның бірінші ретті дербес туындылары осы нүктеде нөлге тең, яғни 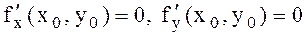болуы немесе бұл туындылардың болмауы қажетті.

Теорема (функцияның экстремумы болуының жеткілікті шарты).

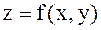функциясының бірінші ретті дербес туындылары 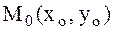нүктесінде 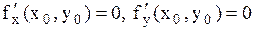шарттарын қанағаттандыратын болсын және осы нүктенің 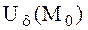маңайында осы функцияның екінші ретті үзіліссіз дербес туындылары бар болсын. 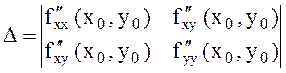деп белгілесек, онда:

1) егер 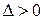және болса, онда 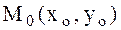максимум нүктесі.

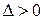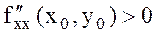2) егер және болса, онда 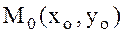минимум нүктесі.

3) егер 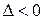болса, онда 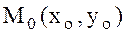нүктесінде функцияның экстремумы жоқ.

Ескерту: Егер 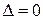болса, онда 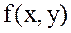функциясының 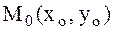нүктесінде экстремумы болуы да болмауы да мүмкін. Сондықтан мұндай жағдайда қосымша зерттеулер жүргізуге тура келеді.

Енді жоғарыда айтылған тұжырымдарға бірнеше мысалдар келтірейік.

Мысал 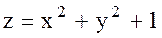функциясын экстремумға зерттейік. Шешуі Дербес туындыларын табайық: 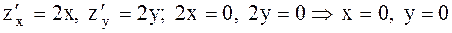. Демек 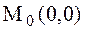нүктесі күдікті нүкте. Енді екінші ретті дербес туындыларын тауып 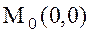нүктесіндегі мәнін есептейміз. 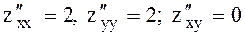. Сонда 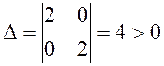. Ендеше 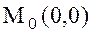нүктесі берілген функцияның минимум нүктесі болады және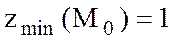

Шартты экстремум. Егер Q аймағында анықталған 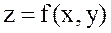функциясы үшін осы аймақтағы 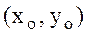нүктесінің маңайындағы 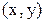-тің барлық мәндерінде 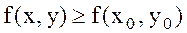немесе 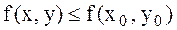теңсіздіктері тек 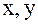байланыс теңдеуі деп аталатын 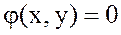теңдеуін қанағаттандыратын осы маңайдың барлық нүктелерінде орындалса, онда функциясының 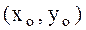нүктесінде шартты минимумы немесе шартты максимумы бар деп айтады. Шартты максимум мен минимум жалпы атпен шартты экстремум деп аталады. Айнымалылары 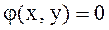шартын қанағаттандыратын 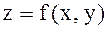функциясын шартты экстремумға зерттеу үшін Лагранж функциясы деп аталатын 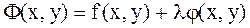функциясын құрамыз. Мұндағы 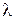саны Лагранж көбейткіші деп аталады. Осы функцияның экстремумы функциясы үшін шартты экстремум болады.

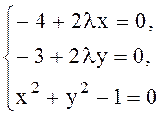Мысал 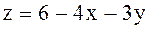функциясының байланыс теңдеуі 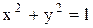болатын шартты экстремумын табу керек. Шешуі 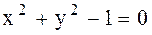теңдеуіне сәйкес шарты экстремумын табу үшін Лагранж функциясын құрамыз: 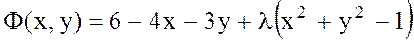.Сонда 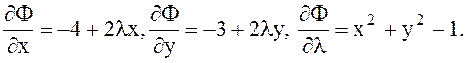. Демек, мына теңдіктер орындалуы керек:

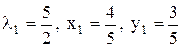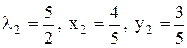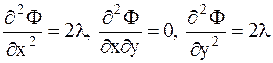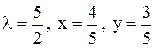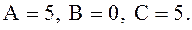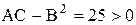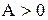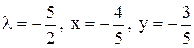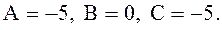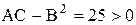Осыдан және .Ал ,сондықтан, егер деп алсақ, Яғни, және . Демек, бұл нүктеде функцияның шартты минимумы бар болады.Ал болса, онда Яғни, және 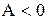. Ендеше бұл нүктеде функцияның шартты максимумы бар болады. Сонымен .

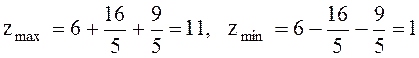10.Сандық қатарлар. Абсолют және шартты жинақты қатарлар.

Анықтама. 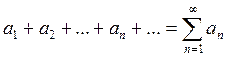, n 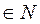өрнегі ақырсыз сандық қатар деп аталады. Ал 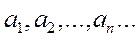сандары қатардың мүшелері, мұндағы 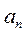- қатардың жалпы мүшесі деп аталады.

Анықтама. Мына қосындыларды жазып алайық: 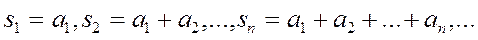Бұл қосындылар қатардың дербес қосындылары деп аталады.

Анықтама. Егер қатардың n 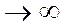да S 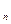деребес қосыныдысының ақырлы шегі S бар болса, онда қатар жинақталатын қатар деп аталып, былай жазылады 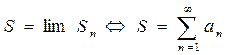. S саны қатардың қосындысы деп аталады. lim 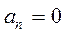болса,қатар жинақты; lim 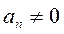, онда қатар жинақсыз.

Енді мүшелері комплекс сандар болатын

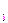u 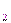+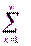u +…= u (1) қатарын және оның мүшелерінің абсолют шамаларынан құралған

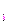| u 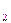|+|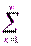u |+…= |u | (2) қатарын қарастырайық. Егер (2) қатар жинақты болса, онда (1)қатар абсолют жинақты қатар деп аталады. Егер (1) қатар жинақты, ал (2) қатар жинақсыз болса, онда (1) қатар шартты жинақты қатар деп аталады.

11.Функционалдық тізбектер және қатарлар. Функционалдық тізбектер мен қатарлар бірқалыпты жинақтылығының жеткілікті белгілері.

Мүшелері нақты х айнымалысының функциясы

Болатын 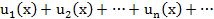қатарын функционалдық қатар дейді. 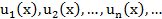функциялары анықталған және 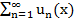қатары жинақты болатын х айнымалының мәндер жиыны функционалдыққатардың жинақталу облысы делінеді. Функционалдыққатардың жинақталу облысы Ох осінің қандай да бір аралығы болады. Алғашқы n мүшелерінің қосындысы 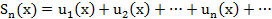болса,

онда 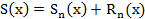. Мұндағы берілген қатардың мүшелерінің қалдығы деп аталады.

Функционалдық тізбектер мен қатарлар бірқалыпты жинақтылығының жеткілікті белгілері.

Егер D облысында (2.3) қатардың барлық мүшелері 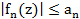шартты қанағаттандырса, мұндағы 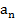-тұрақты оң сандар, сонымен бірге 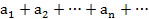(2.6) сандық қатар жинақты болса, берілген (2.3) қатар D облысында бір қалыпты (әрі абсолют) жинақты болады. Дәлелдеу.

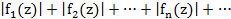қатары D облысының әрбір z нүктесінде жинақты, өйткені оның мүшелері жинақты (2.6) қатардың сәйкес 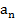мүшелерінен артық емес. Демек, берілген (2.3) қатар D облысының әрбір z нүктесінде абсолют жинақты болады. (2.3) қатардың қосындысы мен бірінші n мүшелерінің қосындысының сәйкес S(z) пен 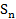(z) белгілеп, мынаны аламыз: 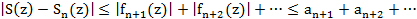(2.7)

Шарт бойынша (2.4) қатар жинақты болатындықтан, оның қалдық мүшесі

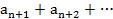қандай болмасын (ε>0) үшін жеткілікті үлкен n N = N=N(ε)-нан бастап ε-нан кем болады. Сөйтіп, (2.7) теңдіктен D облысындағы z нүктесіне тәуелсіз мынаны аламыз:

n <=N = N=N(ε) болғанда 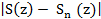< ε.

Бұл (2.3) қатардың D облысында бірқалыпты жинақталатындығын дәлелдейді.

12.Дәрежелік қатарлар және олардың жинақталу облысы.Дәрежелік қатарлар мүшелеп интегралдау және мушелеп диффференциалдау. Функцияларды дәрежелік қатарларға жіктеу.

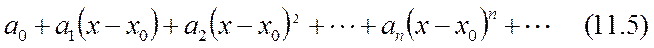
түрінде берілген функциялық қатар дәрежелік қатар деп аталады. Егер 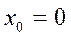болса, онда бұл қатар мына түрге көшеді. .

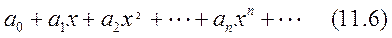Егер (11.6) дәрежелік қатар 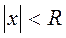болғанда жинақталатын қатар, ал 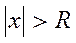болғанда жинақталмайтын қатар болса, онда 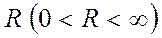саны дәрежелік қатардың жинақталу радиусы немесе жинақталу облысы деп аталады.

Жинақталу радиусын анықтау үшін келесі формулаларды қолданады 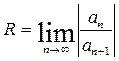және 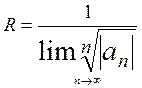. Мысал. 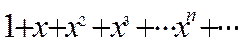дәрежелік қатардың жинақталу радиусы анықтау керек. Шешімі: Мұнда , сондықтан 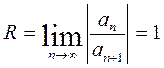. Жинақталу интервалы .

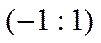Мысал. 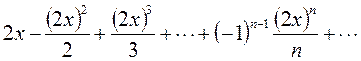функциялық қатардың жинақталу радиусы табу керек.

Шешімі. Мұнда 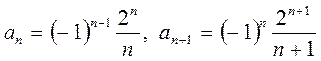, онда 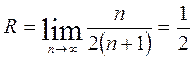. Жинақталу интервалы . Жинақты интервалында дәрежелік қатарды кез келген рет мүшелеп дифференциалдауға және интегралдауға болады.

Дәрежелік x 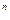функциясының,мұндағы n– еркін алынған 1–ден артық натурал сан,туындысын есептеуге арналған формула мынадай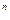: (x )'=nx 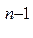(1.6) Бұл ережелер дәлелдеулермен беріледі.Осы ережелерді қолдану арқылы функциялардың туындылары табылады. Дәрежелік қатардың қосындысыныңтуындысын дәрежелік қатарды мүшелеп дифференциалдау арқылы алуға

болады, яғни

,

,

,

,

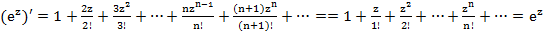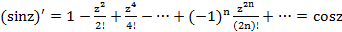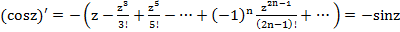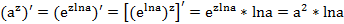
Мүшелеп интегралдау әдіс: Мүшелепинтегралдау формуласы деп келесі теңдікті айтамыз.

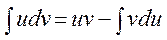(1)

Мүшелепинтегралдау формуласы бір интегралды екінші интеграл арқылы өрнектейді. Бұл формула екінші интегралды есептеу мүмкіндігі болған жағдайда қолданылады. Кей жағдайда соңғы нәтижені алу үшін бөліктеп интегралдау әдісін қайталап қолдануға тура келеді.

1) - түрдегі интеграл

Егер, 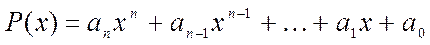-п-дәрежелі көпмүшелік болып, келесі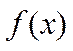 , k=Const, функциялардың бірі болса, онда 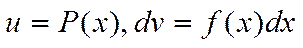деп алып, бөліктеп интегралданады. Бұл жағдайда мүшелепинтегралдау п рет қайталанады.

2) 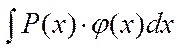-түріндегі интеграл

Егер 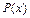-п дәрежелі көпмүшелік, ал 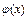-келесі функциялардың бірі болса 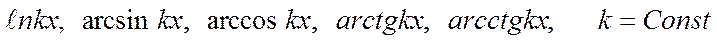, онда 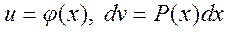. Деп алып, бөліктеп интегралданады.

3) 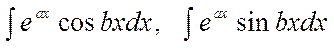түріндегі интегралдар, мұндағы, a,b- тұрақты сандар.

Бұл интегралдар айналымды интеграл деп аталады және екі рет бөліктеп интегралдау арқылы алғашқы интегралы бар теңдеуге келеміз. Интеграл осы теңдеуді шешу арқылы есептеледі.

Мысал1 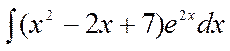интегралын есептеу керек. Шешуі 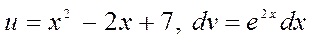деп аламыз. Сонда 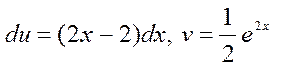.(1)-формуласы бойынша, 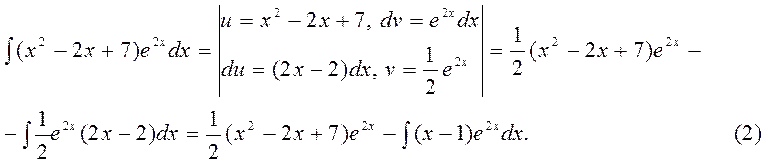(2)

Соңғы интегралға да мүшелепинтегарлдау әдісін пайдаланып

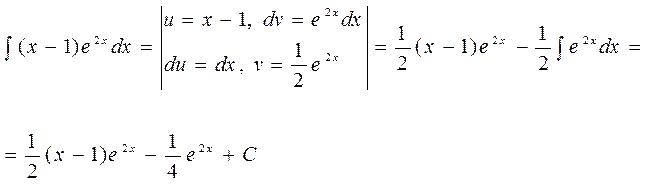
теңдігіне келеміз. Интегралдың осы мәнін (2) теңдігіне қойып, берілген интегалды табамыз:

Соңында,

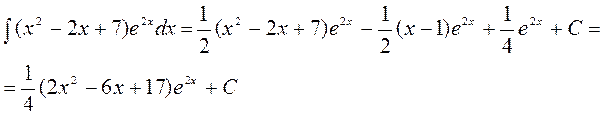
Функцияларды дәрежелік қатарларға жіктеу.

f (x) функциясы a -R <x <a +R аралығында анықталған және кез келген ретті туындылары бар болсын. Тейлор формуласы бойынша

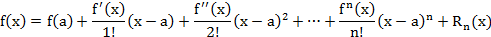
мұндағы 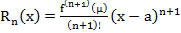, µ=a+ 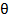(x-a), 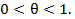Егер n 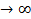, 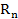(x) 0 болса, онда

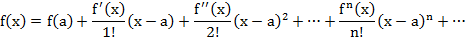
қатары Тейлор қатары деп аталады. 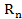(x) - Тейлор қатарының қалдық мүшесі дейді. Егер a =0 болса, онда Тейлор қатары Маклорен қатары деп аталады да

түрінде жазылады. Егер f (x) функциясы (a-R;a+R) аралығында анықталып, кез келген n үшін 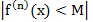теңсіздігі орындалса (мұндағы М-оң тұрақты сан), онда осы функция Тейлор қатарына жіктеледі. Кейбір функциялардың Маклорен қатарына жіктелуін көрсетейік:

1. ()

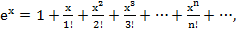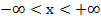2. ()

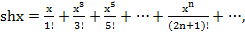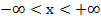3. ()

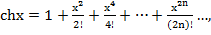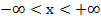4. ()

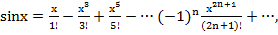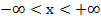5. ()

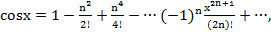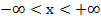6. 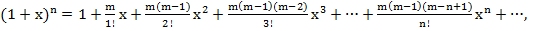Соңғы жіктеуде:

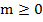болса, онда .

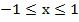-1< 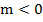болса, онда .

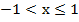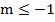болса, онда .

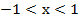13.Қос интегралдаудың негізгі қасиеттері. Қос интегралдауда және үш еселі интегралдауда айнымалыны ауыстыру.

Түйық сызықпен қоршалған, 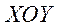жазықтығында жатқан D облысында анықталған үздіксіз 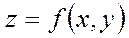функцияны қарастырайық. 0сы облысын n бөлшектерге бөлеміз, ол бөлшектерінің аудандарын 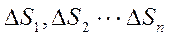деп белгілейік. Әрбір 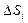бөлшек ішінде жатқан кез келген 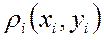нүктені алайық, осы нүктелерге сәйкес 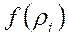функция мәндерін есептеп интегралдық қосындыны құрайық. 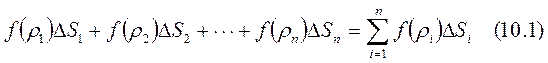осы өрнектің шегі, егер 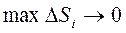, бір тиянақты шекке ұмтылса, онда ол шекті қос интеграл деп атайды, яғни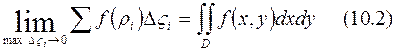

Қос интегралдың қасиеттері.

а) тұрақты көбейткішті интеграл белгісінің сыртына шығаруға болады .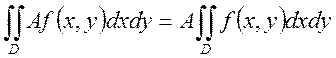

б) 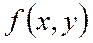және 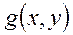функциялардың қосындысының интегралы интегралдар қосындысына тең, яғни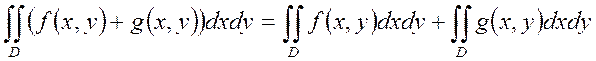

в) Егер интегралдау D облысы екі D₁, және D₂ облысынан құралатын болса, онда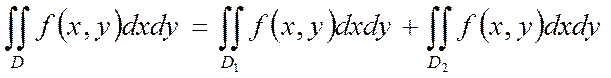

. Қос интегралды есептеу. Айталық D облысы 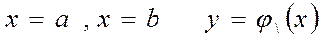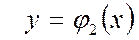сызықтармен шектелген болсын, және 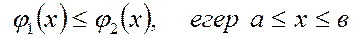.Енді қос интегралдың есептеуі қайталап интегралдауға келтіріледі, яғни 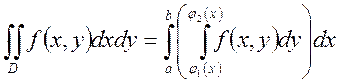мұнда 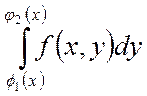-ішкі интеграл деп атайды. Қос интегралды есептегенде бірінші ішкі интегралды есептейді. Бұл жағдайда х-тұрақты деп санайды.

Мысал. 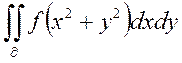қос интегралды есептейік. Мұнда D облысы х=0 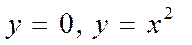сызықтармен шектелген.

Шешімі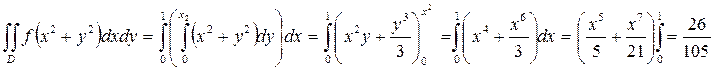

Қос интегралдауда және үш еселі интегралдауда айнымалыны ауыстыру.

Екі еселі интеграл 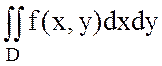қарастырайық.f(x,y) функциясы шенелген тұйық D аймағында үзіліссіз. 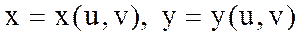(8.4) формулалары арқылы жаңа u және v аргументтеріне көшіп (8.4) теңдеулер жүйесінен 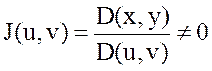деп есептеп, u=u(x,y),v=v(x,y)(8.5) функциялары анықталады. 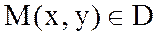нүктесіне u,v координаттар жазықтығында 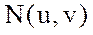нүктесі сәйкес келеді. Онда (8.4) формуласындағы функциялардың дербес туындылары бар болады да, мына анықтауыш 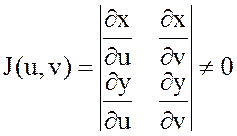,сонда 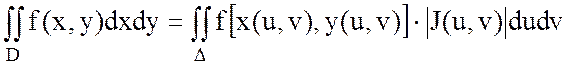(8.6) теңдігі орындалады.J(u,v)-ны x=x(u,v),y=y(u,v) функцияларының Якобинаны деп атайды. Егер (8.4) формуладан полярлық координаталарға көшетін болсақ, яғни 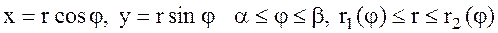(8.7) деп алсақ, онда, (8.7) алмастыруының Якобианы 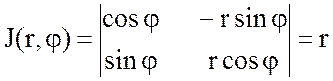екенін ескеріп, 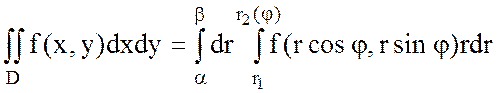(8.8) теңдігіне келеміз.

Мысал 3 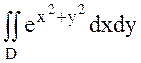, D - бірінші квадрантта жататын 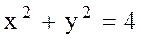дөңгелегінің бөлігі 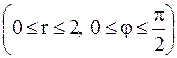. Осы интегралды есептеу керек. Шешуі 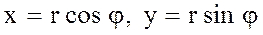формулаларынан ; .

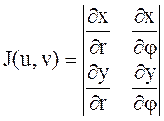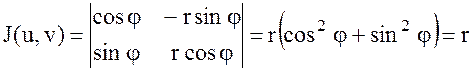Сондықтан, 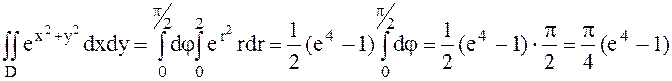Үш еселі интегралдауда айнымалыны ауыстыру.