Жиі қолданылатын шектер

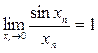– бірінші тамаша шек.

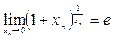- екінші тамаша шек.

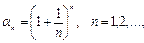тізбегі үшін 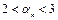теңсіздігі орындалады. Сондықтан 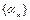жоғарыдан шенелген өспелі тізбек.

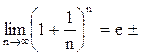
шегі бар болады. 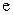санының жуық мәні 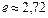болатыны дәлелденген. Бұл сан Непер саны деп аталады.

Жинақты тізбек - шегі бар болатын аn сандар тізбегі.Егер X жиынының әрбір белгіленген x0 нүктесінде fn(x0) сандар тізбегі жинақталса, онда fn(x) функциялар тізбегі X жиынында жинақталады деп айтылады.Теорема

Егер тізбек жинақты болса онда оның тек жалғыз ғана шегі бар. Д/уі Кері жорып жинақты тізбектің шегі бар дейік 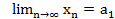және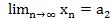

Егер 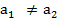болса онда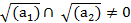

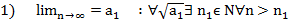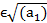
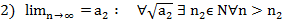x_n

x_n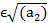

Бұл екі қатынастан n> max {n₁,n₂} болғанда x_n 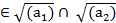шығады. Коши критерийі

Х_n тізбегі R жиынында жинақты болу үшін Хn тізбегінің фундаментальді болуы қажетті және жеткілікті. Қажеттілік айталық х_nтізбегі жинақты және оның шегі а болсын сонда мұның фундаментальді екенін көрсетейік

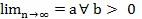∃ n_bϵ N 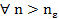=>| x_n-a| =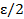

Демек n+p>n_a ушин де фундаментальді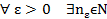

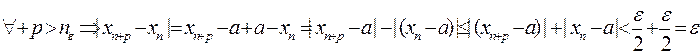Хn функционалды тізбек

2. Функция шегі.Функция шегінің бар болуының Коши критериі.

Егер х₀ нүктесінің кез келген аймағында Х жиынының х₀- ден өзгеше х нүктесі жатса, онда х₀ нүктесін Х жиынының шектік нүктесі деп атайды. Айталық y=f(x) X жиынында анықталсын және х₀ осы Х-тың шектік нүктесі болсын.

Анықтама (Гейне бойынша). Егер х₀ нүктесіне жинақты болатын Х жиынының кез келген 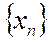тізбегі 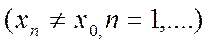бойынша құрылған 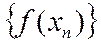тізбегі 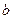санына жинақты болса, онда 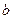санын y=f(x) функциясының х₀ нүктесіндегі (немесе 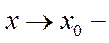дағы) шегі деп атайды. Оны былай жазады:

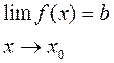немесе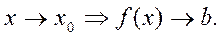

Анықтама. (Коши бойынша). Егер 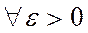сәйкес 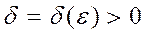саны табылып 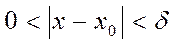шартты қанағаттандыратын х-тің барлық мәндері үшін 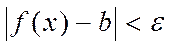теңсіздігі орындалса, онда 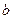санын y=f(x) функциясының х₀ нүктесіндегі шегі деп атайды.

Егер 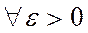санына сәйкес 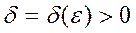саны табылып,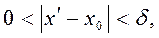 шарттарын қанағаттандыраты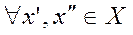н үшін теңсіздігі орындалса, онда 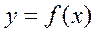функциясы х₀ нүктесінде Коши шартын қанағаттандырады дейді.

Теорема (Коши белгісі). y=f(x)функциясының х₀ нүктесінде тиянақты шегі бар болуы үшін y=f(x) функциясының х₀ нүктесінде Коши шартын қанағаттандыруы қажетті және жеткілікті.

Бірінші тамаша шек

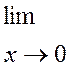
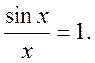
Салдарлар:

1.

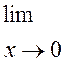
2.

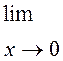
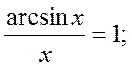
3.

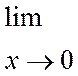
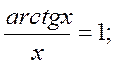
Екінші тамаша шек .

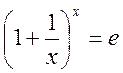Айталық y=f(x) және z=F(y)функциялары берілсін, онда z=F(f(x)) күрделі функция (супперпозиция) болады. Теорема. Егер 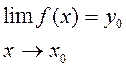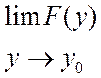шектер бар болса және үшін болса, онда х₀ нүктесінде 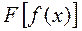күрделі функциясының шегі бар және

= .

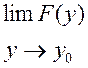3.Үзіліссіз функциялар. Кесіндідегі үзіліссіз функциялардың қасиеті

Аңықтама. y=f(x) функциясы:

a) x₀ нүктенің белгілі бір маңайында аңықталса.

b)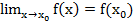

Онда y=f(x) функциясы x₀ нүктеде үзіліссіз деп аталады. Мысал.y = x² функциясы x=0 нүктеде үзіліссіз, өйткені бұл функция біріншіден осы нүктенің аймағында аңықталған, екіншіден 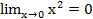, y(0) = 0, яғни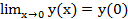

Аңықтама.

y=f(x) функциясы B сандар жиынының (натурал, бүтін, рационал және иррационал сандар жиыны)кез келген нүктесінде үзіліссіз болса, онда бұл y=f(x) функциясы B сандар жиынында үзіліссіз деп аталады.

Теорема. Егер f(x) функциясы [a,b] кесіндісінде үзіліссіз болса, f(x) ол кесіндіде шектелген болады.

Теорема. Егер f(x) функциясы [a,b] кесіндісінде үзіліссіз болса, ол функция сол кесіндіде кем дегенде бір рет өзінің ең үлкен мәнін, бір рет ең кіші мәнін қабылдайды.Мысал. Берілген x₁ және х₂ нүктелеріндегі y= _f(x) функциясының үзіліссіздігін анықтау керек. Егерде олардың ішінде үзілістінүктелер болса, онда оның тегін анықтап, функцияның графигін салу керек.

1)y=3x/x+2; x₁=3,x₂=-2; Шешуі: 1)y=3x/x+2; x₁=3,x₂=-2; Берілген функцияны аргументтің х₁, х₂ мәндерінде жеке-жеке қарастырамыз. х₁=3 нүктесінде функция анықталынған y(3)=3*3/3+2=9/5 және элементарлық функция болғандықтан үзіліссіз.x₂=-2 нүктесінде бөлшектің бөлімі нольге айналатын болғандықтан, функция анықталмаған, сондықтан бұл нүктеде функция үзілісті. Функцияның x₂=-2 нүктесінде оң жақты, сол жақты шектерін есептейміз.

,

.

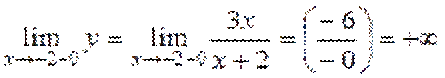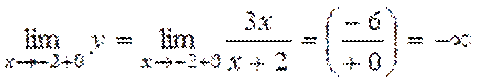Демек, х₂= -2 нүктесі 2-ші текті үзілісті нүкте.

Теорема(4-қ):(Больцано-Коши т/ы)
F(x) функциясы [a; b] кесіндісінде анықталып, үзіліссіз болсын және оның ұштарында әр түрлі таңба қабылдасын.Онда (a;b) аралығында f(x₀)=0 болатын x₀ нүктесі табылады.
Теорема(5-қ): F(x) функциясы [a; b] кесіндісінде анықталып үзіліссіз болсын. Онда f(a) және f(x) нүктелерінің арасында орналасқан кез келген С саны үшін f(x₀)=C болатын x₀∊[a;b] нүктесі табылады.
Теорема(6-қ):(Вейерштрасстың 1-ші т/ы) F(x) функциясы [a; b] кесіндісінде анықталып үзіліссіз болсын. Онда бұл функция сол кесіндіде шенелген.
Теорема(7-қ):(Вейерштрасстың 2-ші т/ы) F(x) функциясы [a; b] кесіндісінде анықталып үзіліссіз болсын. Онда функция [a; b] кесіндісінде өзінің ең үлкен және ең кіші мәндерін қабылдайды, яғни кез келген x₀∊[a;b] нүктесі үшін f(x₁)≤f(x) ≤f(x₂)
теңсіздіктері орындалады. Мысалы:
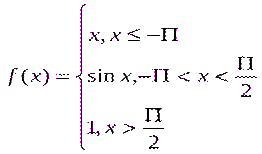Функциясын үзіліссіздікке зерттеп графигін салу керек.Функцияны 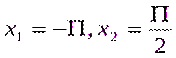нүктелерінде үзіліссіздікке зерттейік, ол үшін сәйкес біржақты шектермен функцияның мәндерін табамыз. 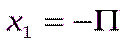нүктесінде:
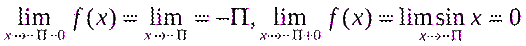
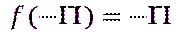Сонымен, бұл нүктеде
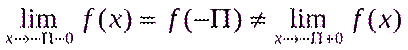яғни, функцияның бірінші текті үзілісі бар және сол жағынан үзіліссіз. F(x) функциясының нүктесіндегі секірмесі:

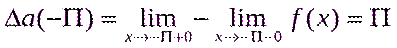
4. Функцияның үзіліс нүктелері және олардың классификациясы.

Функцияның үзіліс нүктелері. Анықтама: x₀ нүктесі F(x) функциясының анықталу аймағына тиісті немесе сол аймақтың шектік нүктесі болсын. Егер F(x) функциясы x₀ нүктесінде үзіліссіз болмаса, онда сол нүкте F(x) функциясының үзіліс нүктесі деп аталады; Үзіліс нүктелер бірінші текті және екінші текті деп бөлінеді; Анықтама: x₀ нүктесі арқылы біржақты 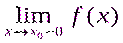және 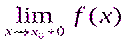шектері бар болса, бірақ олар өзара тең емес немесе біржақты шектер өзара тең, ал функцияның сол нүктедегі мәні біржақты шектермен беттеспесе, онда x0 нүктесі бірінші текті үзіліс нүкте деп аталады; Егер x0 нүктесінде арқылы 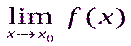шек бар болса, ал f(x₀) анықталмаған немесе 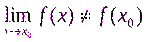болса, онда бұл нүкте жөнделетін үзіліс нүктесі деп аталады. F(x) функциясының, жөнделетін үзіліс нүктесі болмайтын, бірінші текті үзіліс нүктелері функцияның секірме нүктелері деп аталады; Егер x0 - функцияның секірме нүктесі болса, онда 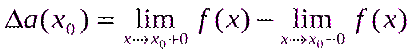айырмасы нөлге тең емес және F(x) функциясының x0 нүктесінде секірмесі деп аталады; Анықтама: егер x0 нүктесінд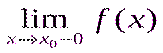е және 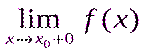біреуі бар болмаса, онда x₀-екінші текті үзіліс нүктесі деп аталады.

5. Дифференциалданатын функциялардың негізгі қасиеттері. Бір айнымалы функция үшін Тейлор формуласы.

Анықтама. Функцияның туындысы мен аргумент өсімшесінің көбейтіндісі дифференциал деп аталады және мына түрде жазады: .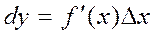

Анықтама. f(x) функциясы x нүктесінде дифференциалданады, егер оның осы нүктеде дифференциалы болса. Егер f(x) функциясы дифференциалданатын болса, онда ол міндетті түрде үзіліссіз болады.

Дифференциалдың қасиеттері:

Негізігі элементар функциялардың туындыларын біле тұрып, біз еш қиындықсыз осы функциялардың дифференциалдарының кестесін құрастыра аламыз.

Айталық, 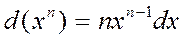, , 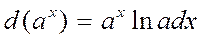т.с.с.

Арифметикалық амалдар нәтижелерінің дифференциалдары:

;

;

.

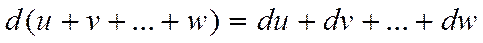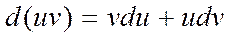Күрделі функцияның дифференциалы:

Айталық, 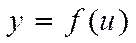және 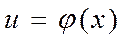- үзіліссіз функциялар және олардың туынддылары: , 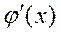. Егер 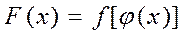белгілесек, онда 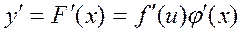. Екі жағын dx-ке көбейтеміз: 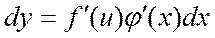, ал 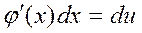, олай болса, .

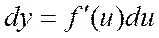Бір айнымалы функция үшін Тейлор формуласы. Айталық y=f(x) функциясы бір аралықта анықталған болып, осы аралықтан алынған х=а нүктесінде n+1-ші ретке дейін туындылары бар болсын. Мұндай шарттар орындалғанда функцияның ролін көпшілік жағдайда n-ші дәрежелі көпмүшелік атқарады Осы көпмүшелікті мына түрінде 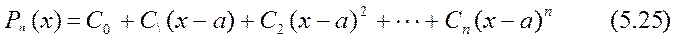алайық. Бұл көмүшелік пен функцияның арасында келесі шарттар орындалатын болсын 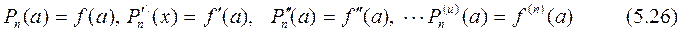Сонғы (5.26) теңдіктер орындалса, онда (5.25) көпмүшелік х=а нүктесінің аймағында y=f(x) функцияны көпмүшелікпен алмастыруға болады.

Көпмүшеліктің С₀ , C₁, C₂ …, C_n коэффициенттерін, (5.26) теңдіктерін пайдаланып, анықтайық. Ол үшін (5.25) көпмүшеліктің туындыларын табайық:

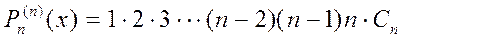
Егер (5.26) теңдіктерін пайдалансақ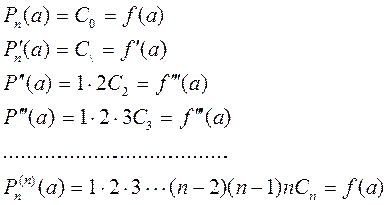

Осы теңдіктерден аталған коэффициенттерді табамыз: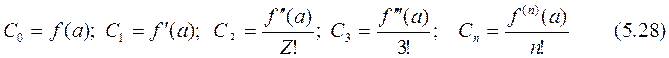

Осы коэффициенттерді (5.28) формулаға қойсақ 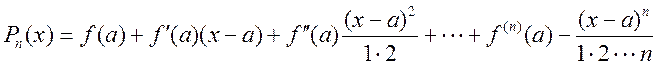формула анықталады.

R_n(x) арқылы f(x) функция мен P_n(x) көпмүшеліктін айырмасын белгілесек

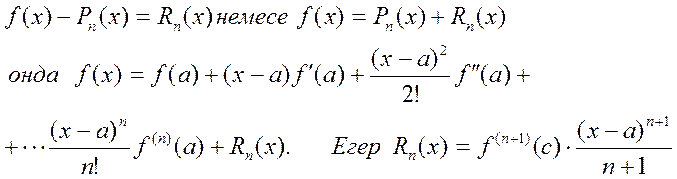белгілесек, мұнда

C=a+ 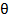(x+a), 0< 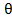<1 онда

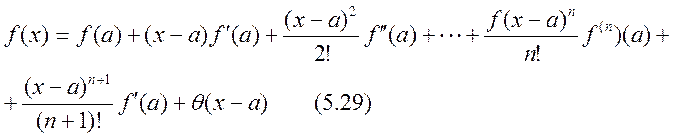Осы формуланы Тейлор формуласы дейді. Мұнда қалдық мүшені 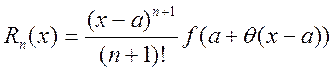түрінде жазылады. Егер Тейлор формуласында а=0 деп алсақ, онда 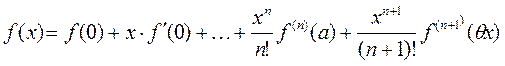(5.30)Бұл формуланы Маклорен формуласы деп айталады. Тейлор формуласын қолдану мысалдар

1) 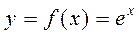функциясы берілсін.

Бұл функцияның 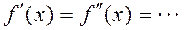== 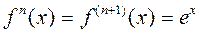онда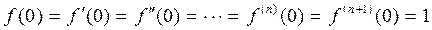

Енді Маклорен формуласын пайдалансақ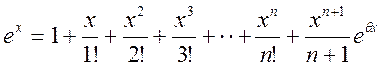

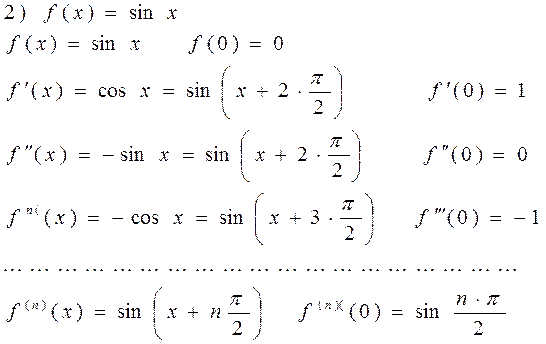
Маклорен формуласы арқылы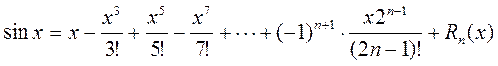

мұнда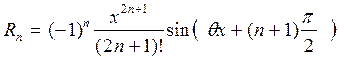

3) f(x)=cosx, онда Маклорен формуласын пайдланып анықтаймыз

Мұнда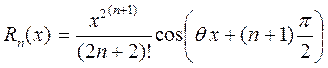

6. Функцияның интегралдануының қажетті және жеткілікті шарттары. Анықталған интегралдың орта мәні туралы теоремалар.

Айталық Х және У нақты сандардан тұратын жиындар болсын.

1-Анықтама. Егер белгілі бір ереже (заң) бойынша Х жиынын құрастыратын әрбір нақты х санына у жиынын құрастыратын сандардың біреуі бірғана у сәйкес келсе, онда Х жиынында бір мәнді y=f(x) функциясы берілген дейді.Мұнда Х жиынын функцияның анықталу немесе берілу облысы, ал У жиынын функцияның мәндерінің облысы, х-ті тәуелсіз айнымалы немесе аргументі дейді.

Үздіксіз f(x) функциясы берілсін. Белгісіз функцияның туындысы 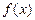-қа тең болсын,- яғни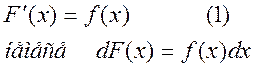

(1) теңдікті қанағаттандыратын F(x) функцияны функцияның алғашқы функциясы деп атайды.

Теорема. Егер F(x) функциясы, 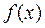функцияның алғашқы функциясы болса, онда F(х)+C да (С- тұрақты сан) алғашқы функция болып табылады, және керісінше, әрбір алғашқы функция F(х)+C түрде сипатталанады.

Туындының қасиеттері арқылы табамыз: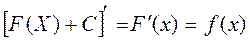

Айталық Ф(х) мына 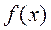функция үшін кезкелген алғашқы функция болсын, онда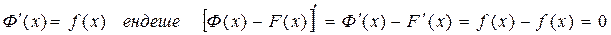

Сондықтан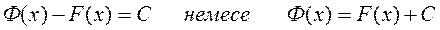

Осы F(х)+C (С-тұрақты сан) өрнекті 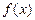функцияның анықталмаған интегралы деп атайды және оны былай белгілейді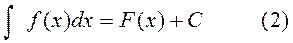

Мұндағы f(x)- интеграл астындағы функция, 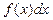- интеграл астындағы өрнек. Алғашқы функцияны табу амалы f(x) функциясын интегралдау деп аталады. Ендеше, интегралдау амалының дұрыс орындалғандығын тексеру үшін алғашқы функцияны дифференциалдап, интеграл астындағы функцияны алсақ болғаны.

Интегралдаудың негізгі ережелері:

1 Егер болса, онда 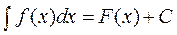, мұндағы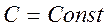

2 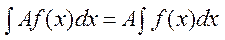, демек тұрақты шаманы интеграл сыртына шығаруға болады.

3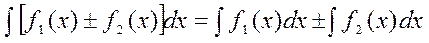

Егер және болса, онда болады. Демек анықталмаған интеграл пішіні интегралдау айнымалысынан тәуелсіз. Мысалы,, өйткені. Екінші мысал: бұл функцияның анықталмаған интегралы.Тексеру:.

Анықталған интегралдың орта мәні туралы теоремалар.

Анықталған интеграл түсінігі.

Анықтама. 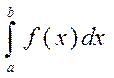анықталған интегралы деп [a, b] аралығында f(x) функциясының алғашқы образының өсімшесін айтамыз:

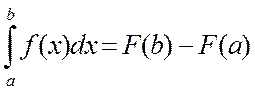
Сонымен қатар, кез келген f(x) функциясы үшін интегралы бар болады (а – кез келген).

Орта мән туралы теорема1. y= f(x) функциясы [a,b] кесіндісінде үзіліссіз болсын, онда бұл кесіндіден 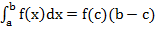теңдігі орындалатындай c нүктесі табылады.

Бұл f(c) мәні функцияның [a,b] аралығындағы орта мәні деп аталады.

Мысал: F(x)= [0,100]

│¹⁰⁰₀ =20/3

Date: 2015-05-22; view: 5807; Нарушение авторских прав