Закон сохранения импульса

Напомним, что систему тел, взаимодействующих только друг с другом и не взаимодействующих ни с какими другими телами, называют замкнутой. Покажем, что векторная сумма импульсов тел, составляющих замкнутую систему, сохраняется.

Рассмотрим сначала случай, когда друг с другом взаимодей­ствуют только два тела.

Обозначим 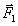, силу, действующую на первое тело со стороны второго, a 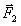— силу, действующую на второе тело со стороны первого. Используя второй закон Ньютона в виде 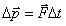, получаем для изменения импульсов тел 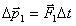, 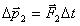. Со­гласно третьему закону Ньютона 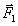= - 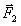, поэтому 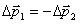. Следовательно, 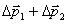= 0. Запишем это соотношение в виде 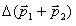= 0.

Мы видим, что при взаимодействии тел друг с другом изме­нение суммы их импульсов равно нулю. А если изменение неко­торой величины равно нулю, то это означает, что эта величина сохраняется.

Пример

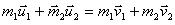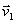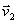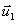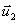Если взаимодействуют друг с другом два тела массами m₁ и m₂. то согласно закону сохранения импульса , где и — скорости тел в какой-либо один момент времени, а и — скоро­сти этих же тел в любой другой момент времени.

Подобным же образом можно доказать, что суммарный импульс сохраняется и для системы, состоящей из нескольких тел, — важно лишь, чтобы эта система тел была замкнутой. Итак, след­ствием второго и третьего законов Ньютона является

№13 Плоское криволинейное движение точки. Норм и танг. ускорение

Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.

Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).

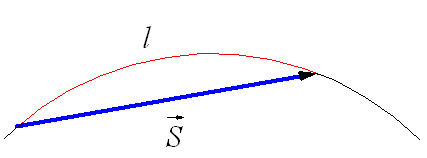
Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.

При движении по криволинейной траектории вектор перемещения 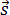направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).

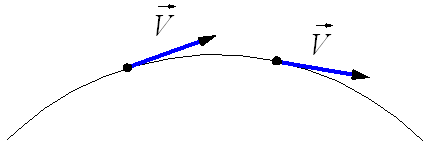
Рис. 1.20. Мгновенная скорость при криволинейном движении.

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:

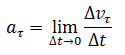
или

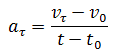
Где v_τ, v₀ – величины скоростей в момент времени t₀ + Δt и t₀ соответственно.

Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.

Нормальное ускорение - это изменение скорости по направлению за единицу времени:

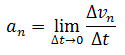
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.

Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.

Полное ускорение при равнопеременном криволинейном движении тела равно:

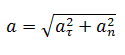
№14 Законы сохран. При упругом и не упругом ударах.

Date: 2015-05-22; view: 467; Нарушение авторских прав