
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тензор скорости деформации
|
|
Теория деформированного состояния.
В общем случае движение твердого недеформируемого тела можно представить суммой поступательного и вращательного движений. Если же тело ещё и деформируется, то движение будет более сложным. Из него можно выделить поступательное и вращательное движения, считая их переносными, а остальное – относительное движение – будет обусловлено только деформацией тела.
Тензор скорости деформации.
Пусть деформируемое тело в некоторый момент имело объем V и было ограничено поверхностью S. Внутри тела имеет место движение частиц. Это движение представлено векторным полем скорости 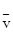 .
.
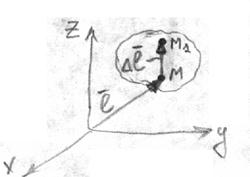
Рассмотрим точку М деформируемого тела вместе с её окрестностью. Положение точки М в трехмерном пространстве задается радиусом вектором 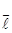 , компоненты (проекции) которого х, у, z.. Бесконечно малая окрестность окружает точку М. Положение произвольной точки М1 в этой окрестности задается дополнительным вектором
, компоненты (проекции) которого х, у, z.. Бесконечно малая окрестность окружает точку М. Положение произвольной точки М1 в этой окрестности задается дополнительным вектором 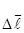 , с компонентами
, с компонентами 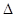 х,
х, 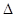 у,
у, 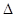 z.
z.
Пусть точка М как точка деформируемого тела имеет в данный момент скорость движения 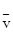 с компонентами вдоль осей координат vx, vy, vz. Скорость точки М1 из области, окружающей точку М, будет отличаться от скорости точки М на величину
с компонентами вдоль осей координат vx, vy, vz. Скорость точки М1 из области, окружающей точку М, будет отличаться от скорости точки М на величину 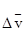 , компоненты которой определяются соотношениями
, компоненты которой определяются соотношениями
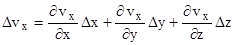
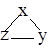 (2. 1)
(2. 1)
Коэффициенты при компонентах вектора 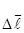 в уравнениях (2.1) образуют так называемый тензор абсолютной производной векторного поля
в уравнениях (2.1) образуют так называемый тензор абсолютной производной векторного поля 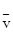
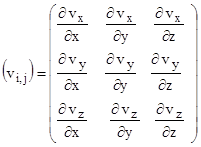 (2.2)
(2.2)
Этот тензор может быть представлены в виде суммы
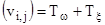 (2.3)
(2.3)
Здесь 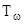 - тензор вращения с компонентами (элементами матрицы)
- тензор вращения с компонентами (элементами матрицы)
 , (2.4)
, (2.4)
а 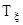 - тензор скорости деформации с компонентами (элементами матрицы)
- тензор скорости деформации с компонентами (элементами матрицы)
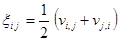 (2.5)
(2.5)
Таким образом движение окрестности точки М сплошной среды состоит из: чистой деформации, определяемой тензором скорости деформации 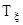 с компонентами (2.5); вращения области относительно точки М, определяемого тензором вращения
с компонентами (2.5); вращения области относительно точки М, определяемого тензором вращения 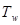 с компонентами (2.4) и поступательного движения, определяемого вектором скорости
с компонентами (2.4) и поступательного движения, определяемого вектором скорости 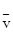 точки М.
точки М.
Компоненты тензора скорости деформации 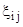 в развернутой форме имеет вид
в развернутой форме имеет вид
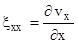
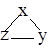 (2.6)
(2.6)
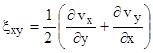
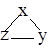 (2.7)
(2.7)
и называются: (2.6) – скоростями удлинения в направлении осей соответственно Х,У,Z, а удвоенные (2.7) – скоростями сдвига в плоскостях соответственно ХОУ, УОZ, ZОХ.
Уравнения (2.6) и (2.7) называются геометрическими или кинематическими соотношениями связи скоростей течения и компонентов тензора скорости деформации.
Тензор скорости деформации имеет вид
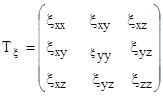 (2.8)
(2.8)
Date: 2015-05-22; view: 561; Нарушение авторских прав