
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дилемма заключенного
|
|
Напомним читателю основные сведения из теории игр.
Представим себе, что в игре участвуют два игрока, каждый из которых владеет некоторым набором «потенциальных» действий. Эти действия называют стратегиями. Пусть α1 ,.., αn — стратегии первого игрока, β1 ,..., βm — стратегии второго игрока. Каждый игрок получает некоторый выигрыш, который зависит от того, какую стратегию он выбрал сам и какую стратегию выбрал его противник.
Игру задают в виде так называемой платежной матрицы, каждой строчке которой соответствует стратегия первого игрока, а каждому столбцу — стратегия второго игрока. В «летке матрицы, находящейся на пересечении i-й строки и j-го столбца, записываются два числа x ij и уij, соответствую-
________________________________________
1 Некоторым сильным умам удавалось почувствовать это. Вот что писал выдающийся шахматист, математик и психолог Эммануил Ласкер свыше 50 лет назад: «...Всякого рода бои отличаются лишь с внешней стороны. Правящие ими законы всегда одинаковы. В этом смысле войной считается конкуренция, погоня за правдой, красотой или счастьем; все эти виды боев похожи друг на друга, а одновременно и на шахматную игру...» (Э. Ласкер. Философия королевской игры. См. Ежи Гижицкий. С шахматами через века и страны. Варшава, 1958, стр, 138).
Конец страницы 8
¯ Начало страницы 9 ¯
щие «выигрышу» первого игрока и «выигрышу» второго игрока:
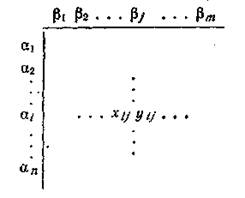
Слово «выигрыш» мы заключили в кавычки, так как возможен случай, когда игрок не получает, а платит, — тогда его «выигрыш» отрицателен. Наиболее изученными являются игры, когда выигрыш одного игрока в точности равен проигрышу другого. Такие игры называют играми с нулевой суммой. В играх с нулевой суммой в платежной матрице обычно пишут одно значение. По договоренности выигрыши игрока 1 читаются с тем знаком, с которым они входят в матрицу, а выигрыши игрока 2 — с противоположным знаком, Например, в матрице
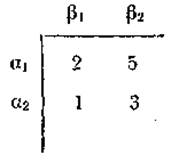
максимальный выигрыш игрока 1 будет при условии, если он выберет первую стратегию, а его противник будет придерживаться второй. В этом случае игрок 2 платит игроку 1 пять единиц.
Если в игровой матрице существует значение выигрыша xij, являющееся максимальным среди минимальных по всем строкам і и одновременно минимальным среди максимальных по всем столбцам j, то стратегии і и j являются наилучшими для каждого игрока с точки зрения достижения ими гарантированного результата и подобная матрица, как говорят, имеет седловую точку. Это означает, что в распоряжении игрока 1 нет ничего лучшего, чем αi, а игрок 2 поступит самым благоразумным образом, если выберет βj. Выбранные таким образом стратегии игроков называются минимаксными стратегиями.
Конец страницы 9
¯ Начало страницы 10 ¯
В матрице
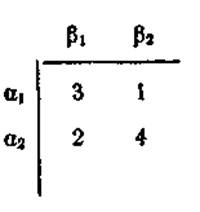
седловой точки нет; для игрока 1 наилучшей стратегией, точнее наилучшей из наихудших, является α2, для игрока 2 — β1. Этот случай не так прост, он требует некоторых рассуждений игроков. В самом деле, игрок 1 убежден в том, что игрок 2 выберет в соответствии с принципом минимакса стратегию β1 так как β1 — лучший ответ на α2. Но в этом случае игроку 1 лучше выбирать α1, чем α2. Если же игрок 2 сумеет повторить это рассуждение, то он. очевидно, выберет β2 а не β1. Тогда игроку 1 следует выбрать α2 и оба игрока будут двигаться по кругу. Выход из этой ситуации заключается в том, что игрокам целесообразно выбирать стратегии случайным образом. Теория игр дает рекомендации, каким образом должен «бросаться жребий»1. Полученные в итоге стратегии называются смешанными, они определяют наилучший исход игры для каждого игрока.
Если же теперь -мы обратимся к играм с ненулевой суммой, то характер рассуждений, которыми по необходимости пользуются игроки, существенно усложнится. В играх с ненулевой суммой в каждую клетку матрицы мы должны поместить не одно, а два значения платежей: xij и уij. если игрок 1 выбрал стратегию αi, а игрок 2 — βj, то первый получает выигрыш xij, а второй — у ij. Естественно интерпретировать отрицательные значения выигрышей как проигрыши.
Рассмотрим платежную матрицу следующей игры:

Известна следующая интерпретация матриц такого типа, приписываемая американскому исследователю Таккеру, утверждавшему, что эпизод этот взят из жизни.
______________________________________________
1 Только маленьким детям свойственно прятать камешек то в одной, то в другой руке попеременно.
Конец страницы 10
¯ Начало страницы 11 ¯
Двух подозреваемых берут под стражу и изолируют друг от друга. Прокурор убежден в том, что они совершили серьезное преступление, но не имеет достаточных доказательств для предъявления им обвинения. Каждому из них говорится, что у него имеются две альтернативы: признаться в преступлении или не признаться. Если оба не признаются, то прокурор предъявит им обвинение в каком-либо незначительном преступлении, например, в незаконном хранении оружия, и оба они получат небольшое наказание; если они оба признаются, то суд накажет обоих, но прокурор не потребует самого строгого приговора; если же один признается, а другой будет упорствовать, то признавшемуся приговор будет смягчен за выдачу сообщника, в то время как непризнавшийся получит полную меру.
Если эту ситуацию сформулировать в сроках заключения, то игра, которую предлагает прокурор, сводится к следующей матрице:
Заключенный 2
| Заключенный 1 | Непризнание β1 | Признание β2 | |
| Непризнание α1 | по 1 году каждому | 10 лет первому и 3 месяца второму | |
| Признание α2 | 3 месяца первому и 10 лет второму | по 7 лет каждому |
Перед каждым заключенным стоит вопрос: признаться или не признаться?
Рассмотрим эту ситуацию с позиции игрока 1. Если он не признается (α1) и не признается его партнер (β1), то оба они получат по году. Но если партнер не признается, то первому игроку выгоднее признаться (α2), так как в этом случае ok будет осужден только на три месяца. Но, с другой стороны, если окажется, что партнер признался, то оба они получат по семь лет каждый. Парадокс, который возникает в этой ситуации, обычно понимается как противоречие между собственными интересами игрока и коллективным интересом «шайки»: каждому в отдельности выгоднее признаться, но обоим вместе выгоднее «держаться». Однако можно предположить, что причины парадокса кроются в логической структуре оснований для принятия решений, с которыми оперирует игрок, находящийся в такой ситуации. Это будет показано ниже в главе 2.
Отметим, что полное исключение из рассуждений игроков моральных и этических моментов не облегчает их положения. Дилемма не снимается также предварительной договоренно-
Конец страницы 11
¯ Начало страницы 12 ¯
стью игроков или их контактами в ходе следствия. Ведь каждый в итоге принимает решение независимо и может нарушить любую конвенцию: каждому выгодно разорвать договор, обманув сообщника, хотя риск достаточно велик и рациональная позиция диктует, что договор должен соблюдаться.
Широкий интерес психологов и теоретиков игр к дилемме заключенного объясняется загадочной природой этого парадокса. По мнению американского специалиста А. Раппопорта, дилемма заключенного принадлежит к тем парадоксам, которые «иногда появляются на интеллектуальном горизонте как предвестник важных научных и философских открытий».
По-видимому, дилемма заключенного действительно является плодотворной моделью, с помощью которой можно получить интересные психологические результаты. В книге, которая так и называется «Дилемма заключенного», А. Раппопорт описывает результаты экспериментов, проведенных со студентами Мичиганского университета, которые «разыгрывают дилемму заключенного» много раз. Статистическая обработка этих данных показывает широкую вариацию выборов в различных парах игроков: в протоколах партий встречаются выборы стратегий как «признания», так и «непризнания».
Однако развитие игровой модели такого типа и богатый экспериментальный материал представляют скорее ценность для психологов, как не совсем обычный инструмент установления индивидуальных психологических различий игроков, нежели для логиков, изучающих мыслительную деятельность в конфликте. Статистические модели поведения, вытекающие из экспериментов с дилеммой, не могут объяснить внутренний механизм этой деятельности, поскольку внешняя неопределенность выбора решения в ситуации дилеммы, возведенная в ранг внутренней закономерности, препятствует проникновению в логический механизм, порождающий эту неопределенность. Пока же отметим, что традиционная теория игр не умеет отвечать на многие вопросы, поставленные практикой конфликтного взаимодействия: в лучшем случае она обосновывает методику экспериментов, по результатам которых мы можем прояснить психологические аспекты поведения.
Date: 2015-04-23; view: 641; Нарушение авторских прав