Мышление игроков и принципы теории игр

Рефлексивная схематизация конфликта, как показывает последний пример, позволяет обнаруживать некоторые чистые и, в известном смысле, универсальные механизмы мыш-

______________________________________

¹ Заметим кстати, зеркало — мощнейшая моделирующая машина, более быстродействующая и емкая, чем цифровые вычислительные машины.

­ Конец страницы 32 ­

¯ Начало страницы 33 ¯

ления игроков. Это дает сразу два преимущества: во-первых, становится ясной логическая подоплека принимаемых решений, во-вторых, создаются благоприятные условия для самостоятельного исследования социально-этической и психологической оболочки конфликта. В итоге и исследователь операций, и психолог получают в свое распоряжение инструмент объективного анализа некоторых сторон субъективного мира игрока.

Рефлексивный анализ позволяет получить также логическое обоснование некоторых теоретико-игровых принципов. Как известно, большая часть результатов теории игр получена на основе принципа максимина. Этот принцип диктует выбор такого решения, при котором обеспечивается гарантированный результат: выбирается стратегия, приводящая К наилучшему из наихудших результатов. Исследователи операций пользуются этим принципом при построении игровых моделей конфликта, не располагая обычно сведениями о том, действительно ли ситуация требует применения этого принципа, порожденного представлением о превосходстве противника. Какова же та «внутренняя модель», при которой игрок вынужден «использовать» принцип максимина?

Рассмотрим игрока X, который представлен суммой вида:

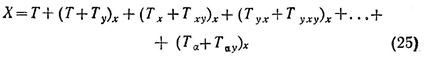
где α — некоторая последовательность индексов х и у. В каждом «кадре», на которые разбита сумма (25), элемент, принадлежащий X, отражается в элементе, принадлежащем игроку Y. Игрок имеет такую модель противника, что любая мысль X (с его точки зрения) имитируется противником X, который, исходя из результата имитации, и принимает решение. Такая модель, естественно, отдает предпочтение «наименее пагубной мысли». Игрок X будет руководствоваться той стратегией, заведомо зная которую и приняв наилучшее решение, игрок У нанесет X наименьший ущерб. А это и есть принцип максимина. Таким образом, выражение (25) представляет собой исходную логическую форму, порождающую один из основных принципов теории игр.

Другая схема рассуждения, основанная на представлении о доминировании над противником, приводит к другим сетованиям для принятия решения. Пусть игрок X изображается суммой

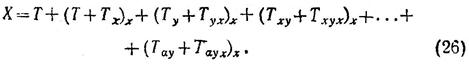
­ Конец страницы 33 ­

¯ Начало страницы 34 ¯

В этом выражении в каждом кадре-слагаемом элемент, принадлежащий Y, отражается в элементе, принадлежащем игроку X, а не наоборот, как в выражении (25). Любая мысль, пришедшая в голову Y, имитируется игроком X ( с точки зрения X). В этом случае игрок X может принять оптимальное решение, рассматривая своего противника как своеобразную «интеллектуальную» природу, на которую X может воздействовать. Как будет показано в следующей главе, игрок, изображенный подобным образом, может стремиться управлять процессом принятия решения своего противника. Эта схема рассуждения порождает принцип, который можно назвать принципом превосходства. Рассуждения людей в конфликтах протекают преимущественно по этому принципу.

В принципе любой конфликт можно истолковать как «игру с участием дьявола». Тогда три указанных типа рассуждений приобретают любопытную окраску: (24) — «мы оба— дьяволы»; (25) — «он — дьявол», (26) — «я — дьявол».

Для конечного числа элементов суммы вида (24), (25) и (26) непереводимы друг с друга. Это значит, что рефлексивное изображение игроков может быть использовано для определения того, какой принцип используется игроком. Можно определить также, каким принципом следует пользоваться, если мы располагаем информацией о рассуждениях игрока, которые можно схематизировать в виде конечной суммы. Разумно предположить, что эти соображения могут принести пользу исследователям операций.

­ Конец страницы 34 ­

¯ Начало страницы 35 ¯