
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сферическое движение твердого тела
|
|
Сферическим называется движение твердого тела имеющего одну неподвижную точку. Тело D совершает сферическое движение, относительно
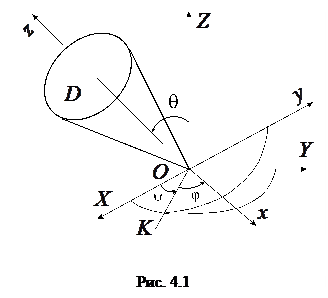 неподвижной точки О (рис. 4.1). Точки тела D движутся по сферам с центром в точке О.
неподвижной точки О (рис. 4.1). Точки тела D движутся по сферам с центром в точке О.
Для характеристики сферичес-кого движения тела введем две ортогональные системы отсчета c началом координат в неподвижной точке О: неподвижную ОХУZ и под-вижную Охуz, связанную с телом D и движущуюся вместе с ним относительно точки О. Прямая OK являющаяся линией пересечения плоскости ХOУ с плоскостью хOу, называется линией узлов.
Положение подвижной системы Охуz относительно неподвижной ОХУZ можно задать с помощью углов Эйлера: угла прецессии 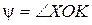 , угла собственного вращения
, угла собственного вращения 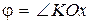 и угла нутации
и угла нутации 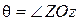 . Следовательно, для задания сферического движения твердого тела необходимо задать углы Эйлера как функции времени:
. Следовательно, для задания сферического движения твердого тела необходимо задать углы Эйлера как функции времени:
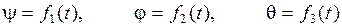 . (4.1)
. (4.1)
Уравнения (4.1) называются уравнениями сферического движения твердого тела.
 При изменении только угла
При изменении только угла 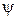 тело D будет вращаться вокруг оси ОZ с угловой скоростью
тело D будет вращаться вокруг оси ОZ с угловой скоростью 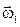 ; при изменении только угла
; при изменении только угла 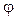 тело D будет вращаться вокруг оси Оz с угловой скоростью
тело D будет вращаться вокруг оси Оz с угловой скоростью 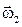 ; при изменении только угла
; при изменении только угла 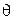 тело D будет вращаться вокруг линии узлов ОК с угловой скоростью
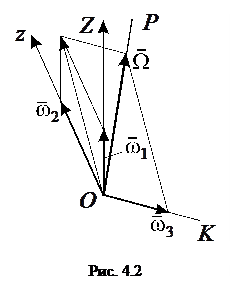
тело D будет вращаться вокруг линии узлов ОК с угловой скоростью  (рис. 4.2). При движении тела D все три угла Эйлера меняются одновременно, и результирующее движение будет вращательным движением с мгновенной угловой скоростью
(рис. 4.2). При движении тела D все три угла Эйлера меняются одновременно, и результирующее движение будет вращательным движением с мгновенной угловой скоростью
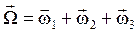 . (4.2)
. (4.2)
Прямая ОР вдоль которой направлен вектор мгновенной угловой скорости 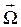 результирующего вращения называется мгновенной осью вращения тела.
результирующего вращения называется мгновенной осью вращения тела.
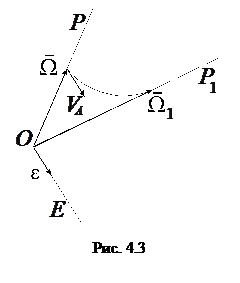 При сферическом движении тела D мгновенная ось ОР меняет свое положение в пространстве, при этом вектор мгновенной угловой скорости
При сферическом движении тела D мгновенная ось ОР меняет свое положение в пространстве, при этом вектор мгновенной угловой скорости 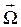 изменяется не только по величине, но и по направлению (рис. 4.3).
изменяется не только по величине, но и по направлению (рис. 4.3).
Угловым ускорением тела в момент времени t называется вектор
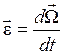 . (4.3)
. (4.3)
Но согласно (1.2) скорость точки А – конца вектора мгновенной угловой скорости 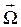
 .
.
Следовательно, при сферическом движении тела вектор углового ускорения 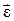 в каждый момент времени направляется как скорость
в каждый момент времени направляется как скорость 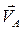 конца вектора мгновенной угловой скорости
конца вектора мгновенной угловой скорости 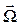 тела и прикладывается в непо-движной точке О (рис. 4.3 ):
тела и прикладывается в непо-движной точке О (рис. 4.3 ):
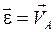 . (4.4)
. (4.4)
Прямая ОЕ вдоль которой направлен вектор углового ускорения 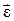 называется осью углового ускорения.
называется осью углового ускорения.
При сферическом движении тела направления векторов 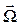 и
и 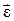 не совпадают.
не совпадают.
 Для определения скорости произвольной точки М тела D проведем из неподвижной точки О в точку М радиус вектор
Для определения скорости произвольной точки М тела D проведем из неподвижной точки О в точку М радиус вектор 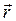 . Тогда согласно (1.2) и (2.18)
. Тогда согласно (1.2) и (2.18)
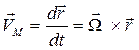 , (4.5)
, (4.5)
поскольку вектор 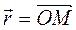 постоянный по модулю, так как расстояние между точками О и М абсолютно твердого тела при движении не изменяется.
постоянный по модулю, так как расстояние между точками О и М абсолютно твердого тела при движении не изменяется.
Следовательно, при сферическом дви-жении тела скорость любой его точки опре-деляется как её вращательная скорость вокруг мгновенной оси.
Для определения величины скорости точки М опустим из этой точки на мгновенную ось ОР перпендикуляр hp. Тогда
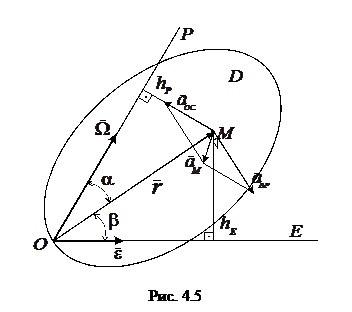
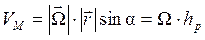 . (4.6)
. (4.6)
Вектор 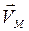 направлен согласно (4.5) перпендикулярно плос-кости, проходящей через точку М и мгновенную ось вращения ОР в направлении
направлен согласно (4.5) перпендикулярно плос-кости, проходящей через точку М и мгновенную ось вращения ОР в направлении 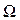 (
(
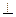 hp рис. 4.4).
hp рис. 4.4).
Для определения ускоре-ния точки М тела при сфери-ческом движении вычислим производную по времени от равенства (4.5):
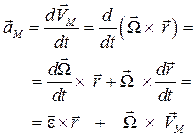
или
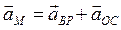 . (4.7)
. (4.7)
Здесь
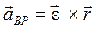 (4.8)
(4.8)
называется вращательным ускорением точки М; а
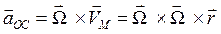 (4.9)
(4.9)
- осестремительным ускорением точки М.
Следовательно, ускорение любой точки при сферическом движении определяется как геометрическая сумма её вращательного и осестреми-тельного ускорений.
Модули осестремительного и вращательного ускорений определяются по формулам:
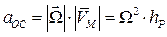 ; (4.10)
; (4.10)
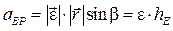 , (4.11)
, (4.11)
где 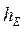 - величина перпендикуляра опущенного из точки М на ось углового ускорения ОЕ. На рис. 4.5 вектор осестремительного ускорения
- величина перпендикуляра опущенного из точки М на ось углового ускорения ОЕ. На рис. 4.5 вектор осестремительного ускорения 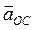 направлен согласно (4.9) из точки М к мгновенной оси ОР (вдоль hp). Вектор вращательного ускорения
направлен согласно (4.9) из точки М к мгновенной оси ОР (вдоль hp). Вектор вращательного ускорения  согласно (4.8) направлен в точке М перпендикулярно плоскости, походящей через эту точку и ось углового ускорения ОЕ в направлении
согласно (4.8) направлен в точке М перпендикулярно плоскости, походящей через эту точку и ось углового ускорения ОЕ в направлении 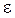 .
.
Вектор полного ускорения 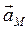 точки при сферическом движении определяется диагональю параллелограмма, построенного на векторах
точки при сферическом движении определяется диагональю параллелограмма, построенного на векторах 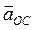 и
и  как на сторонах. Поэтому модуль
как на сторонах. Поэтому модуль 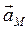 определяется по формуле
определяется по формуле
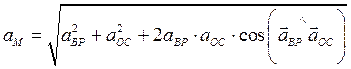 . (4.12)
. (4.12)
Date: 2015-05-19; view: 1175; Нарушение авторских прав