Эффект Допплера

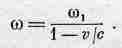
Рассмотрим теперь ряд других эффектов, связанных с движением источника. Пусть источник представляет собой покоящийся атом, колеблющийся со своей обычной частотой ш₀. Частота наблюдаемого света тогда будет равна w₀. Но возьмем другой пример: пусть такой же атом колеблется с частотой w₁ и в то же время весь атом, весь осциллятор как целое движется со скоростью v по направлению к наблюдателю. Тогда истинное движение в пространстве будет таким, как изоб­ражено на фиг. 34.10,а. Используем наш обычный прием и до­бавим ст, т. е. сместим всю кривую назад и получим колебания, представленные на фиг. 34.10,6. За промежуток времени т осциллятор проходит расстояние vт, а на графике с осями х' и у' соответствующее расстояние равно (с-v)t. Таким образом, число колебаний с частотой ш1, которое укладывалось в интер­вал Ат, на новом чертеже укладывается теперь уже в интервал Dt = (1-v/c) Dt; осцилляции сжимаются, и, когда новая кривая будет двигаться мимо нас со скоростью с, мы увидим свет более высокой частоты, увеличенной за счет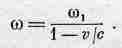
фактора сокращения (1-v/c). Итак, наблюдаемая частота равна

(34.10)

Можно, конечно, объяснить этот эффект и другими спосо­бами. Пусть, например, тот же атом испускает не синусоидаль­ную волну, а короткие импульсы (пип, пип, пип, пип) с неко­торой частотой ш1. С какой частотой мы будем их воспринимать? Первый импульс к нам придет спустя определенное время, а второй импульс придет уже через более короткое время, потому что атом за это время успел к нам приблизиться. Следова­тельно, промежуток времени между сигналами «пип» сокра­тился за счет движения атома. Анализируя эту картину с геометрической точки зрения, мы придем к выводу, что час­тота импульсов увеличивается в 1/(1-v/c) раз.

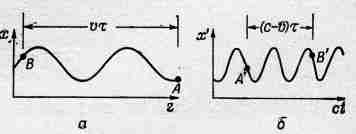
Фиг, 34.10. Движение осциллято­ра в плоскости х—z и в плоскости x'—t.

Будет ли наблюдаться частота w= w₀/(1-v/c), если атом с собственной частотой ш₀ движется со скоростью v к наблюда­телю? Нет. Нам хорошо известно, что собственная частота дви­жущегося атома w₁ и частота покоящегося атома w₀ — не одно и то же из-за релятивистского замедления хода времени. Так что если w₀ — собственная частота покоящегося атома, то час­тота движущегося атома будет равна

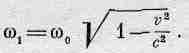
(34.11)

Поэтому наблюдаемая частота w окончательно равна

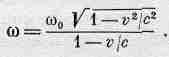
(34.12)

Изменение частоты, возникающее в таком случае, назы­вается эффектом Допплера: если излучающий объект движет­ся на нас, излучаемый им свет кажется более синим, а если он движется от нас, свет становится более красным.

Приведем еще два других вывода этого интересного и важ­ного результата. Пусть теперь покоящийся источник излучает с частотой w₀, а наблюдатель движется со скоростью v к источ­нику. За время t наблюдатель сдвинется на новое расстояние vt от того места, где он был при t = 0. Сколько радиан фазы пройдет перед наблюдателем? Прежде всего, как и мимо любой фиксированной точки, пройдет ю₀t, а также некоторая добавка за счет движения источника, а именно vtk₀ (это есть число ради­ан на метр, умноженное на расстояние).

Отсюда число радиан за единицу времени, или наблюдаемая частота, равно w₁=w₀+k₀v. Весь этот вывод был произведен с точки зрения покоящегося наблюдателя; посмотрим, что уви­дит движущийся наблюдатель. Здесь мы снова должны учесть разницу в течении времени для наблюдателя в покое и движе­нии, а это значит, что мы должны разделить результат на Ö(1-v2/с²). Итак, пусть k₀ есть волновое число (количество ради­ан на метр в направлении движения), а со₀ — частота; тогда частота, регистрируемая движущимся наблюдателем, равна

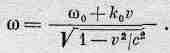
(34.13)

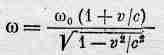
Для света мы знаем, что k₀ = w₀/c. Следовательно, в рас­сматриваемом примере искомое соотношение имеет вид

(34.14)

и, казалось бы, не похоже на (34.12)!

Отличается ли частота, наблюдаемая при нашем движении к источнику, от частоты, наблюдаемой при движении источника к нам? Конечно, нет! Теория относительности утверждает, что обе частоты должны быть в точности равны. Если бы мы были достаточно математически подготовлены, то могли бы убедиться, что оба математических выражения в точности равны! В действительности требование равенства обоих выражений часто используется для вывода релятивистского замедления времени, потому что без квадратных корней равенство сразу нарушается.

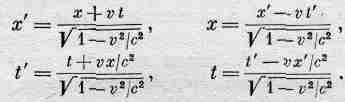
Раз уж мы начали говорить о теории относительности, при­ведем еще и третий способ доказательства, который покажется, пожалуй, более общим. (Суть дела остается прежней, ибо не играет роли, каким способом получен результат!) В теории от­носительности имеется связь между положением в пространстве и временем, определяемым одним наблюдателем, и положением и временем, определяемым другим наблюдателем, движущимся относительно первого. Мы уже выписывали эти соотношения (гл. 16). Они представляют собой преобразования Лоренца, прямые и обратные:

(34.15)

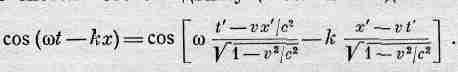
Для неподвижного наблюдателя волна имеет вид cos(cot- kx); все гребни, впадины и нули описываются этой формой. А как будет выглядеть та же самая физическая волна для движущегося наблюдателя? Там, где поле равно нулю, любой наблюдатель при измерении получит нуль; это есть релятивистский инвариант. Следовательно, форма волны не меняется, нужно только напи­сать ее в системе отсчета движущегося наблюдателя:

Произведя перегруппировку членов, получим

(34.16)

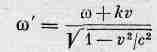
Мы снова получим волну в виде косинуса с частотой w' в ка­честве коэффициента при t' и некоторой другой константой k' — коэффициентом при х'. Назовем k' (или число колебаний на 1 м) волновым числом для второго наблюдателя. Таким об­разом, движущийся наблюдатель отметит другую частоту и другое волновое число, определяемые формулами

(34.17)

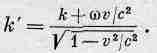
(34.18)

Легко видеть, что (34.17) совпадает с формулой (34.13), полу­ченной нами на основании чисто физических рассуждений.

§ 7. Четырехвектор (w, k)

Соотношения (34.17) и (34.18) обладают весьма интересным свойством: новая частота w' линейно связана со старой частотой w и старым волновым числом k, а новое волновое число представ­ляется в виде комбинации старого волнового числа и частоты. Далее, волновое число есть скорость изменения фазы с расстоя­нием, а частота — скорость изменения фазы со временем, и сами соотношения обнаруживают глубокую аналогию с пре­образованиями Лоренца для координаты и времени: если со сопоставить с t, a k с х/с², то новое w' сопоставляется с t', a k' — с координатой х'/с². Иначе говоря, при преобразовании Лоренца w и k изменяются так же, как t и х. Эти величины w и k составляют так называемый четырехвектор. Четырехкомпонентная величина, преобразующаяся как время и координа­ты, и есть четырехвектор. Здесь все правильно, за исключением одного — четырехвектор имеет четыре компоненты, а у нас фигурируют только две! Как уже говорилось, со и k подобны времени и одной координате пространства; для введения двух остальных координат надо изучить распространение света в трехмерном пространстве.

Пусть задана система координат х, у, z и волна движется в пространстве с волновым фронтом (фиг. 34.11). Длина волны есть К, а направление распространения волны не совпадает ни с одной осью координат.

Фиг. 34.11. Плоская волна, движущаяся под углом.

Какой вид имеет формула движения для такой волны? Ответ очевиден: это cos (a>t-ks), где k = 2п/X a s (расстояние вдоль направления движения вол­ны) — проекция вектора положения на направление движе­ния. Запишем это следующим образом: пусть r есть вектор точки в пространстве, тогда s есть г-е_k, где e_k — единичный вектор в направлении движения волны. Иначе говоря, s равно rcos(r-e_k), проекции расстояния на направление движе­ния. Следовательно, наша волна описывается формулой cos(wt-ke_k•r).

Оказывается очень удобным ввести вектор k, называемый волновым вектором', величина его равна волновому числу 2p/l, а направление совпадает с направлением распространения волны

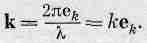
(34.19)

Благодаря введению этого вектора волна приобретает вид cos(wt-k•r), или cos(wt-k_xx-k_yy-k_zz). Выясним смысл про­екций k, например k_x. Очевидно, k_x есть скорость изменения фазы в зависимости от координаты х. Фиг 34.11 подсказывает нам, что фаза меняется с ростом х так, как если бы вдоль х бежала волна, но соответствующая ей длина волны оказывается больше по величине. «Длина волны в направлении х» больше истинной на множитель, равный секансу угла a между осью х и направле­нием движения истинной волны:

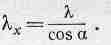
(34.20)

Следовательно, скорость изменения фазы, обратно пропорцио­нальная X_х, в направлении х оказывается меньше на множитель cos а; но этот же множитель содержит и k_x, равный модулю k, умноженному на косинус угла между k и осью х!

Итак, мы выяснили смысл волнового вектора, описывающего распространение волны в трехмерном пространстве. Четыре величины со, k_x, k_y, k_z преобразуются в теории относительности как четырехвектор, причем со соответствует времени, a k_x, ky, k_z соответствуют х, у и z и компонентам четырехвектора.

Еще раньше, когда мы занимались теорией относительности (гл. 17), мы выяснили, что из четырехвекторов можно соста­вить релятивистское штрихованное произведение. Взяв вектор положения x_m (где m, нумерует четыре компоненты — время и три пространственные) и волновой вектор k_m (где и. снова про­бегает четыре значения), образуем штрихованное произведе­ние х_m и k_m, записываемое в виде S'k_m х_m. Это произведение есть инвариант, не зависящий от выбора системы коор­динат. Согласно определению штрихованного произведения,

можно записать S'k_m х_m. следующем виде:

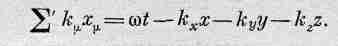
(34.21)

Поскольку k_m есть четырехвектор, то, как мы уже знаем, Sk_mx_m есть инвариант по отношению к преобразованиям Лорен­ца. Под знак косинуса в нашей формуле для плоской волны вхо­дит именно это произведение, и оно обязано быть инвариантом от­носительно преобразований Лоренца. У нас не может появиться формула, у которой под знаком косинуса стоит неинвариантная величина, потому что мы знаем, что значение фазы не зависит от выбора системы координат.

Date: 2015-05-19; view: 494; Нарушение авторских прав