Определение «кажущегося» движения

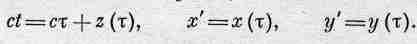
Написанное выше уравнение можно упростить довольно инте­ресным способом. Опустим неинтересный для нас постоянный член R₀/c (это означает только, что мы изменяем начало отсчета времени t на постоянный отрезок) и запишем

(34.5)

Нам нужно найти х' и у' как функции t, а не т, и это достигается следующим образом: как подсказывает уравнение (34.5), нужно взять истинное движение заряда и добавить время т, умножен­ное на константу (скорость света). На фиг. 34.2 показано, что это означает. Возьмем истинную траекторию заряда (показанную слева) и представим себе, что по мере движения заряд удаляется от точки Р со скоростью с (здесь нет каких-либо релятивистских сокращений и подобных вещей; это просто математическое до­бавление ст). Таким путем получится новая траектория, где по оси абсцисс отложено ct, как показано на рисунке справа. (На рисунке изображена траектория довольно сложного движения в плоскости, но движение может происходить не только в плокости.)

Фиг. 34.2. Геометрический способ определения x'(t) из уравнения (34.5.).

Смысл приведенной процедуры состоит в том, что гори­зонтальное расстояние в правой части фиг. 34.2 в отличие от левой оказывается равным не z, a z+cт, т. е. ct. Мы нашли, таким образом, график изменения х' (и у') в зависимости от t\ Осталось только определить ускорение на кривой, т. е. продиф­ференцировать ее дважды. Отсюда окончательно заключаем: чтобы найти электрическое поле движущегося заряда, нужно взять траекторию движения и заставить двигаться каждую ее точку от точки наблюдения со скоростью с; полученная кривая дает положения х' и у' как функцию t. Ускорение на этой кривой определит электрическое поле в зависимости от t. Можно, если угодно, представить себе, что вся эта «твердая» кривая дви­жется вперед со скоростью с сквозь плоскость зрения, так что точка пересечения с плоскостью зрения имеет координаты х' и у'. Ускорение этой точки и определит электрическое поле! Полученное решение будет не менее точно, чем формула, из ко­торой мы исходили,— это просто ее геометрическое представ­ление.

Если источник совершает относительно медленное движение, как, например, медленно колеблющийся вверх и вниз осцилля­тор, то при растягивании этого движения со скоростью света получится простая синусоидальная кривая. Отсюда можно получить формулу для поля, создаваемого осциллирующим заря­дом, которую мы видели неоднократно.

Более интересный пример — это электрон, движущийся по окружности со скоростью, близкой к скорости света. Если на­блюдатель находится в плоскости движения электрона, запазды­вающее движение x'(t) имеет для него вид, изображенный на фиг. 34.3. Что это за кривая? Если мы представим себе радиус-вектор, проведенный из центра окружности к заряду, и если мы продолжим эти радиальные линии чуть-чуть за заряд (совсем капельку, если заряд движется быстро), то мы придем к точке, которая движется со скоростью света с. Поэтому результирую­щее движение есть движение заряда, прикрепленного к ко­лесу, которое катится назад (без скольжения) со скоростью с;

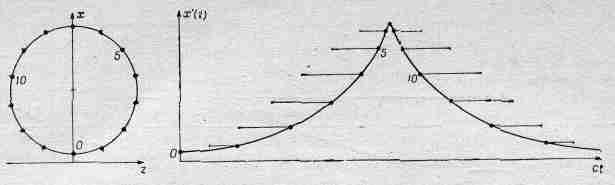
Фиг. 34.3. Кривая зависимости х' (t) для частицы, вращающейся по окружности с постоянной скоростью v = 0,94c.

это дает нам кривую, очень похожую на циклоиду, называется она гипоциклоидой.

Когда заряд движется по окружности со скоростью, близкой к скорости света, пики на кривой становятся очень острыми, а при скорости, равной скорости света, они были бы бесконечно острыми. «Бесконечно острые» пики! Очень интересно; это зна­чит, что вблизи такого пика вторая производная очень велика. Один раз в течение каждого периода возникает мощный и резкий импульс электрического поля. Ничего похожего в случае нере­лятивистского движения не бывает, там электрическое поле в те­чение всего периода принимает значения примерно одного и того же порядка. Вместо этого в случае больших скоростей там воз­никают резкие импульсы электрического поля с интервалом вре­мени 1/Т₀, где Т ₀ — период обращения. Это сильное электриче­ское поле излучается в узком конусе около направления движе­ния заряда. Когда же заряд удаляется от точки наблюдения Р, производная кривой мала и излучение в направлении Р очень слабое.

Date: 2015-05-19; view: 425; Нарушение авторских прав