Дифракционная решетка

На практике равенство фаз осцилляторов или антенн дости­гается с помощью проводов и всяких специальных устройств. Возникает вопрос, можно ли и как создать подобную систему для света. Сейчас мы еще не умеем делать маленькие радиостан­ции оптической частоты в буквальном смысле слова, соединять их крохотными проволочками и устанавливать для всех них одинаковые фазы. Однако есть другой очень простой способ, позволяющий добиться этой цели.

Предположим, у нас имеется большое количество парал­лельных проводов, отстоящих друг от друга на расстоянии d, и источник радиоволн, расположенный очень далеко, практи­чески на бесконечности. Этот источник создает электрическое поле у каждой из проволочек с одной и той же фазой, (Можно взять и объемную систему проводов, но мы ограничимся плоской системой.) Тогда внешнее электрическое поле будет двигать электроны взад и вперед в каждой проволочке, в результате они становятся новыми излучателями. Такое явление называется рассеянием: свет от некоторого источника вызывает движение электронов в среде, а оно в свою очередь генерирует собствен­ные волны. Поэтому достаточно взять ряд проволок на равном расстоянии друг от друга, подействовать на них радиоволнами от удаленного источника, и получается нужная нам система без всяких специальных контуров и т. п. Если лучи падают по нор­мали к плоскости проводов, фазы колебаний будут одинаковыми и возникнет та картина, о которой говорилось выше. Так, при расстоянии между проволочками, превышающем длину вол­ны, максимальная интенсивность рассеяния получается в на­правлении нормали и в других направлениях, определяемых формулой (30.6.).

Точно такое же устройство годится и для света! Только вместо проволок берут стеклянную пластинку и наносят на нее ряд штрихов так, чтобы каждый из них рассеивал свет иначе, чем остальная поверхность пластинки. Если затем направить на пластинку пучок света, то каждый штрих станет источником, а если расстояние между штрихами будет достаточно мало, но не меньше одной длины волны (практически таких малых рас­стояний все равно невозможно добиться), возникает удивитель­ное явление: лучи идут через пластинку не только по прямой, но и под конечным углом к нормали, зависящим от расстояния между штрихами! Устройства такого типа действительно суще­ствуют и широко используются, их называют дифракционными решетками.

Одна из разновидностей дифракционных решеток представ­ляет собой обычную стеклянную пластинку, прозрачную и бес­цветную, с нацарапанными на ней штрихами. Число штрихов на 1 мм зачастую достигает нескольких сотен, а расстояние между ними выдерживается с большой точностью. Действие такой решетки можно наблюдать, посылая сквозь нее с помощью про­ектора узкую вертикальную полоску света (изображение щели) на экран. Помещая решетку на пути света так, чтобы штрихи были расположены вертикально, мы увидим на экране ту же самую полоску света, но по сторонам от нее, кроме того, будут и другие полосы, окрашенные в разные цвета. Разумеется, мы получили не что иное, как уширенное изображение щели; угол 6 в (30.6) зависит от l, и разная окраска света, как мы знаем, соответствует разным частотам и разным длинам волн. Самой большой видимой длиной волны обладает красный свет; в силу условия d sinq=l ему соответствует наибольшее q. И мы дей­ствительно обнаруживаем, что на экране красная полоса лежит дальше всех от центра изображения! С другой стороны должна быть такая же полоса; и в самом деле, мы видим на экране вторую полосу. Выражение (30.6) имеет еще одно решение с т =2. На соответствующем ему месте на экране видно какое-то рас­плывчатое слабое пятно, а дальше в сторону чуть заметен еще целый ряд слабых полосок.

Только что мы сказали, что максимумы всех порядков долж­ны иметь одинаковую интенсивность, а у нас интенсивность получается разная, и, более того, правый и левый максимумы первого порядка отличаются по своей яркости! Причина здесь кроется в том, что решетки изготовляются особым способом, чтобы как раз и получался подобный эффект. Как это делается? Если бы дифракционные решетки имели бесконечно тонкие штри­хи, расположенные на строго равном расстоянии друг от друга, то интенсивности максимумов всех порядков были бы одинако­вы. Но фактически, хотя мы пока разобрали только простейший случай, мы могли бы также взять систему, состоящую из пар антенн, причем в каждой паре установили бы определенную раз­ность фаз и интенсивности. Тогда можно было бы получить раз­ную интенсивность у максимумов разных порядков. На дифрак­ционную решетку часто наносят не ровные, а пилообразные штрихи. Специально подбирая форму «зубцов», можно увели­чить интенсивность спектра данного порядка по отношению к остальным. В практической работе с решетками желательно иметь максимальную яркость в одном из порядков. Мы отло­жим пока весьма сложное объяснение этих фактов, скажем только, что такие решетки оказываются гораздо более полез­ными в применениях.

До сих пор мы рассматривали случай, когда фазы всех источ­ников равны. Однако полученная нами формула (30.3) годится также и тогда, когда сдвиг фаз j каждого источника по срав­нению с предыдущим постоянен и равен а. Это означает, что антенны должны быть соединены по схеме, обеспечивающей небольшой сдвиг фазы между ними. Можно ли создать подобное устройство для света? Да, и очень просто. Пусть источник света находится на бесконечности и свет падает на решетку под не­которым углом, равным q_вх (фиг. 30.4); рассмотрим рассеянный пучок света, выходящий под углом q_ВЫХ (q_вых — это наш старый угол q, а q_вх нужен для создания разности фаз у источников).

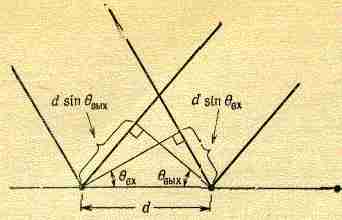
Фиг. 30.4.Разность хода двух лучей, отраженных соседними ли­ниями решетки, равна

d sinq_вых — dsinq_вх.

Пучок света от бесконечно удаленного источника падает сначала на первый штрих, затем на второй и т. д., сдвиг фазы света, по­падающего на два соседних штриха, есть a = - d sinq_ВХ/l. Отсюда получаем формулу для дифракции света, падающего на решетку под некоторым углом:

(30.7)

Попытаемся найти направление максимальной интенсивности в этом случае. Условие возникновения максимума по-прежнему состоит в том, что j должно быть числом, кратным 2p. Здесь следует отметить несколько интересных моментов.

Прежде всего, рассмотрим весьма интересный случай, соот­ветствующий m=0; когда d меньше l, тогда m=0 и других ре­шений не возникает. Тогда получаем sinq_вх = sinq_вых,

т. е. рассеянный луч выходит в том же направлении, что и перво­начальный луч, падающий на дифракционную решетку. Но не следует думать, что свет просто «проходит насквозь». Мы ведь говорим о других лучах. Свет, проходящий насквозь, идет от первоначального источника, а мы имеем в виду свет, возникающий при рассеянии. Получается так, что рассеянный пу­чок света идет в том же направлении, что и первоначальный; более того, оба пучка могут интерферировать друг с другом, о чем мы расскажем в последующих главах.

В нашем случае имеется еще одно возможное решение. При заданном q_вх угол q_вых может быть равен дополнительному к q_вх углу (p-q_вх). Таким образом, кроме луча в направлении падающего пучка света, возникает еще один луч. Легко заме­тить, что его направление подчиняется правилу: угол падения равен углу рассеяния. Этот луч мы назовем отраженным.

Так мы подходим к пониманию основного механизма процес­са отражения: падающий свет возбуждает движение атомов отражающего тела, а оно в свою очередь генерирует новую волну, и одно из направлений рассеянной волны (единственное для расстояния между рассеивателями, малого по сравнению с длиной волны) таково, что угол падения луча света равен углу, под которым выходит отраженный луч!

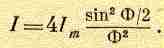
Перейдем теперь к особому случаю, когда d®0. Имеется, скажем, плотное тело конечных размеров. Потребуем еще, чтобы разность фаз между соседними рассеивателями стремилась к нулю. Иначе говоря, будем ставить все новые и новые антенны в промежутках между прежними, так что разности фаз будут становиться все меньше по мере уменьшения расстояния до соседних антенн, но общее число антенн пусть растет так, что полная разность фаз между первой и последней антенной остает­ся постоянной. Посмотрим, как видоизменится формула (30.3), если полная разность фаз n j остается постоянной (пусть nj =Ф), а число n и фаза j стремятся соответственно к бесконечности и нулю. Теперь значение j так мало, что sin j = j, и если учесть также, что n²I₀ есть интенсивность в центре максимума I _m, то мы получим

(30.8)

На фиг. 30.2 показан ход этой предельной зависимости.

В данном случае дифракционная картина в общих чертах получается такой же, как и для конечного промежутка d>l, те же боковые максимумы, нет только максимумов высших по­рядков. Когда все рассеиватели находятся в фазе, возникает максимум в направлении q_вых =0 и минимум при D =l, в точ­ности как для конечных d и n. Таким образом, оказывается воз­можным рассмотреть непрерывное распределение рассеивателей или осцилляторов, используя интегралы вместо сумм.

Для примера возьмем длинную линию, составленную из ос­цилляторов, которые колеблются вдоль нее (фиг. 30.5). Такое устройство дает максимальную интенсивность в направлении, перпендикулярном нити. Кверху и книзу от экваториальной плоскости имеется небольшая интенсивность, но она очень мала. Пользуясь этим результатом, перейдем к более сложному устрой­ству. Предположим, у нас имеется целый набор нитей, каждая из которых излучает в экваториальной плоскости. Если мы на­ходимся в центральной плоскости, перпендикулярной всем проволокам, интенсивность излучения набора длинных линий в разных направлениях определяется так же, как и в случае бесконечно коротких линий,— нужно сложить вклады от всех длинных проволок.

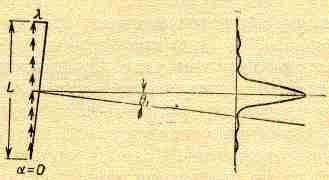
Фиг. 30.5. Распределение интен­сивности излучения непрерывной линии осцилляторов имеет высокий центральный максимум и много­численные слабые боковые максиму­мы.

Вот почему вместо крошечных решеток — антенн, которые мы рассматривали, можно было бы использо­вать решетки с длинными и узкими щелями. Каждая из длинных щелей излучает в своем собственном направлении не вверх и не вниз, а только перпендикулярно щели, и, поставив их рядом друг с другом в горизонтальной плоскости, мы получим интер­ференцию.

Таким образом, можно создать еще более сложные устрой­ства, размещая рассеиватели по линии, в плоскости или в про­странстве. Сначала мы располагали рассеиватели на линии, а затем проанализировали случай, когда они заполняют полосу; для получения ответа каждый раз нужно было просуммировать вклады отдельных рассеивателей. Последний принцип справед­лив во всех случаях.

Date: 2015-05-19; view: 453; Нарушение авторских прав