
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Гипотеза де Бройля и ее экспериментальные подтверждения
|
|
Французский ученый Луи де Бройль (1892—1987), гипотеза об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.
Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия Е и импульс p, а с другой — волновые характеристики — частота n и длина волны l. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов:
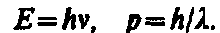 (1)
(1)
Соотношение (1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемой по формуле де Бройля:
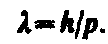 (2)
(2)
Это соотношение справедливо для любой частицы с импульсом р.
Вскоре гипотеза де Бройля была подтверждена экспериментально. В 1927 г. американские физики К. Дэвиссон (1881—1958) и Л. Джермер (1896—1971) обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки — кристалла никеля, — дает отчетливую дифракционную картину. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов, а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (2). В дальнейшем формула де Бройля была подтверждена опытами П. С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (энергия»50 кэВ) через металлическую фольгу (толщиной»1 мкм).
Удалось экспериментально подтвердить в 1948 г., что волновые свойства присущи не только потоку большой совокупности электронов, но и каждому электрону в отдельности, российскому физику В. А. Фабриканту (р. 1907). Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других (промежуток времени между двумя электронами в 104 раз больше времени прохождения электроном прибора), возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов, в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой частице в отдельности.
Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описывать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рассчитываемой по формуле де Бройля (2). Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких,как электронография и нейтронография, а также к возникновению новой отрасли науки — электронной оптики.
Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что перед нами универсальное явление, общее свойство материи. Но считается, что макроскопические тела проявляют только одну сторону своих свойств — корпускулярную — и не проявляют волновую.
Представление о двойственной корпускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы e и частотой n волн де Бройля:
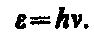 (3)
(3)
Это свидетельствует о том, что соотношение между энергией и частотой в формуле (3) имеет характер универсального соотношения, справедливогокак для фотонов, так и для любых других микрочастиц.
Соотношение неопределенностей
Согласно соотношению неопределенностей Гейзенберга, микрочастица (микрообъект) не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (рх, pу, pz), причем неопределенности этих величин удовлетворяют условиям
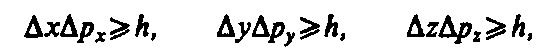 (1)
(1)
т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.
Из соотношения неопределенностей (1) следует, что, например, если микрочастица находится в состоянии с точным значением координаты (D x = 0), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной (D px ® ¥), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта.
| Рис. 1 |
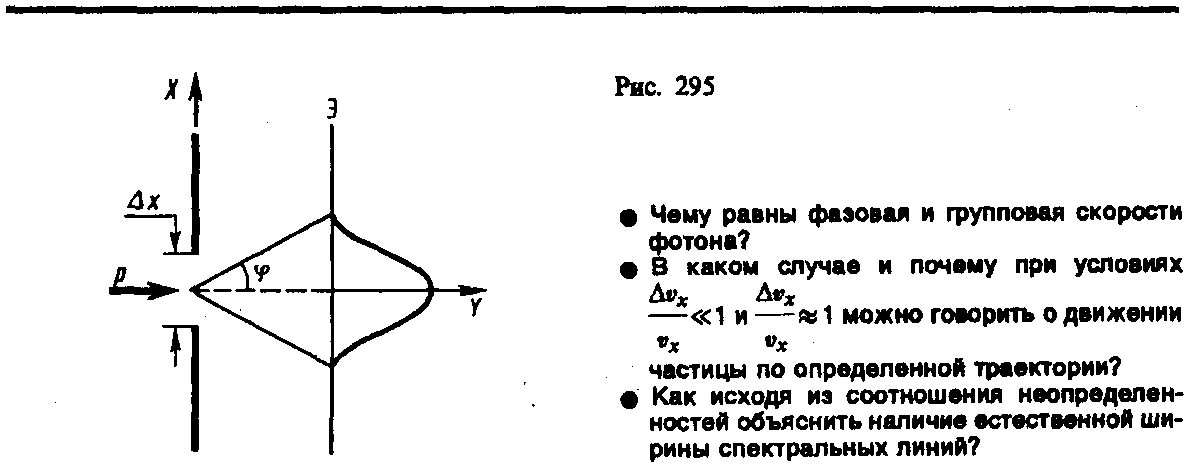 Соотношение неопределенностей действительно вытекает из волновых свойств микрочастиц. Пусть поток электронов проходит через узкую щель шириной D х, расположенную перпендикулярно направлению их движения (рис. 1). Так как электроны обладают волновыми свойствами, то при их прохождении через щель, размер которой сравним с длиной волны де Бройля l электрона, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране (Э), характеризуется главным максимумом, расположенным симметрично оси Y, и побочными максимумами по обе стороны от главного (их не рассматриваем, таккак основная доля интенсивности приходится на главный максимум).
Соотношение неопределенностей действительно вытекает из волновых свойств микрочастиц. Пусть поток электронов проходит через узкую щель шириной D х, расположенную перпендикулярно направлению их движения (рис. 1). Так как электроны обладают волновыми свойствами, то при их прохождении через щель, размер которой сравним с длиной волны де Бройля l электрона, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране (Э), характеризуется главным максимумом, расположенным симметрично оси Y, и побочными максимумами по обе стороны от главного (их не рассматриваем, таккак основная доля интенсивности приходится на главный максимум).
До прохождения через щель электроны двигались вдоль оси Y, поэтому составляющая импульса рх= 0, так что D px =0, а координата х частицы является совершенно неопределенной. В момент прохождения электронов через щель их положение в направлении оси Х определяется с точностью до ширины щели, т. е. с точностью D х. В этот же момент вследствие дифракции электроны отклоняются от первоначального направления и будут двигаться в пределах угла 2 j (j — угол, соответствующий первому дифракционному минимуму). Следовательно, появляется неопределенность в значении составляющей импульса вдоль оси X равна:
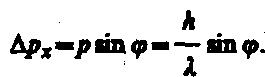 (2)
(2)
Из теории дифракции известно, что первый минимум соответствует углу j, удовлетворяющему условию
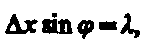 (3)
(3)
где D х — ширина щели, а l — длина волны де Бройля. Из формул (2) и (3) получим
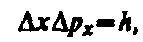
где учтено, что для некоторой, хотя и незначительной, части электронов, попадающих за пределы главного максимума, величина D рx ³ р sin j. Следовательно, получаем выражение
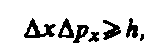
т. е. соотношение неопределенностей (1).
Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.
Соотношение неопределенностей, отражая специфику физики микрочастиц, позволяет оценить, например, в какой мере можно применять понятия классической механики к микрочастицам, в частности, с какой степенью точности можно говорить о траекториях микрочастиц. Известно, что движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Выразим соотношение неопределенностей (1) в виде
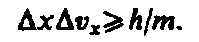 (4)
(4)
В квантовой теории рассматривается также соотношение неопределенностей для энергии Е и времени t, т. е. неопределенности этих величии удовлетворяют условию
 (5)
(5)
Подчеркнем, что D Е — неопределенность энергии некоторого состояния системы, D t — промежуток времени, в течение которого оно существует. Следовательно, система, имеющая среднее время жизни D t, не может быть охарактеризована определенным значением энергии; разброс энергии D E = h /D t возрастает с уменьшением среднего времени жизни. Из выражения (5) следует, что частота излученного фотона также должна иметь неопределенность D n = D E / h, т. е. линии спектра должны характеризоваться частотой, равной n ± D E / h.
Волновая функция и ее статистический смысл
Немецкий физик М. Борн (1882—1970) в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая Y(х, у, z, t). Эту величину называют также волновой функцией (или Y-функцией). Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:
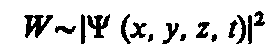 (1)
(1)
(|Y|2=YY*, Y * — функция, комплексно сопряженная с Y). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени t в области с координатами х и x+dx, у и y+dy, z и z+dz.
Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому — с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах. Вероятность нахождения частицы в элементе объемом d V равна
 (2)
(2)
Величина
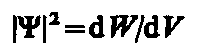
(квадрат модуля Y-функции) имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z. Таким образом, физический смысл имеет не сама Y-функция, а квадрат ее модуля |Y|2, которым задается интенсивность волн де Бройля.
Вероятность найти частицу в момент времени t в конечном объеме V, согласно теореме сложения вероятностей, равна
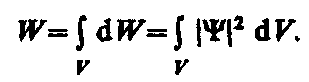
Так как |Y|2d V определяется как вероятность, то необходимо волновую функцию Y нормировать так, чтобы вероятность достоверного события обращалась в единицу, если за объем V принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей
 (3)
(3)
где данный интеграл (3) вычисляется по всему бесконечному пространству, т. е. по координатам х, у, z от –¥ до ¥. Таким образом, условие (3) говорит об объективном существовании частицы в пространстве.
Чтобы волновая функция являлась объективной характеристикой состояния микрочастиц, она должна удовлетворять ряду ограничительных условий. Функция Y, характеризующая вероятность обнаружения действия микрочастицы в элементе объема, должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).
Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями Y1, Y2,..., Y n,... то она также может находиться в состоянии Y, описываемом линейной комбинацией этих функций:
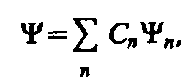
где С n (n =1, 2,...)—произвольные, вообще говоря, комплексные числа. Сложение волновых функций (амплитуд вероятностей), а не вероятностей (определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.
Волновая функция Y, являясь основной характеристикой состояния микрообъектов, позволяет в квантовой механике вычислять средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние á r ñ электрона от ядра вычисляют по формуле
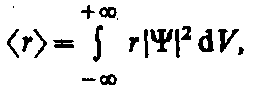
Date: 2015-05-19; view: 2582; Нарушение авторских прав