
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Бозон Хиггса
|
|
Четвертого июля 2012 года произошло событие, имеющее выдающееся значение для современной физики: в ЦЕРНе — Европейском центре ядерных исследований — было объявлено об открытии новой частицы, свойства которой, как осторожно заявляют авторы открытия, соответствуют ожидаемым свойствам теоретически предсказанного элементарного бозона Стандартной модели физики частиц. Следуя распространенной терминологии, этот бозон часто называют бозоном Хиггса, хотя это название не вполне адекватно. Как бы то ни было, речь идет об открытии одного из центральных объектов фундаментальной физики, не имеющего аналогов среди известных элементарных частиц и занимающего уникальное место в физической картине мира.
минимальная версия теории микромира носит название Стандартной модели. Эта теория описывает все известные элементарные частицы и все известные взаимодействия между ними. Бозон Хиггса был единственным не открытым до последнего времени элементом Стандартной модели. Мы назвали эту модель минимальной именно потому, что других элементарных частиц в ней нет. В частности, в ней имеется один и только один бозон Хиггса, и он является элементарной, а не составной частицей. Большинство аспектов Стандартной модели, за исключением той ее части, которой принадлежит бозон Хиггса, проверены в многочисленных экспериментах, и главная задача Большого адронного коллайдера — выяснить, действительно ли в природе реализуется минимальный вариант теории и насколько полно эта теория описывает микромир программа поиска бозона Хиггса была с самого начала одной из главных, если не самой главной, на Большом адронном коллайдере. В ходе выполнения этой программы и была открыта новая частица. Она довольно тяжелая по меркам физики микромира. В этой области науки массу измеряют в единицах энергии, имея в виду связь E = mc 2 между массой и энергией покоя. В качестве единицы энергии используют электронвольт (эВ) — энергию, которую приобретает электрон, проходя разность потенциалов 1 вольт, и производные единицы — МэВ (миллион электронвольт, 106 эВ), ГэВ (миллиард электронвольт, 109 эВ), ТэВ (триллион электронвольт, 1012 эВ). Масса электрона в этих единицах равна 0,5 МэВ, протона — примерно 1 ГэВ, масса самой тяжелой известной элементарной частицы, t -кварка, — 173 ГэВ. Так вот, масса новой частицы составляет 125–126 ГэВ (неопределенность связана с погрешностью измерений). Вообще, всё, что сейчас известно о новой частице, согласуется с ее интерпретацией как бозона Хиггса, предсказанного Стандартной моделью макромира. В рамках этой модели можно вычислить как вероятность рождения бозона Хиггса в протон-протонных столкновениях, так и вероятности его распадов — и тем самым предсказать число ожидаемых событий. Эти предсказания и подтверждаются экспериментом, конечно в пределах экспериментальных погрешностей. Эти погрешности пока велики, да и измеренных величин пока совсем немного. Тем не менее трудно сомневаться в том, что открыт именно бозон Хиггса или что-то очень похожее на него. Особенно если учесть, что распады H → γγ и H → 4 l должны быть очень редкими: на два фотона распадается 2 из 1000 бозонов Хиггса, а на две e + e – и/или μ+μ– пары — 1 из 10 000.
Общим свойством физических теорий, будь то ньютонова механика, механика специальной теории относительности, квантовая механика или теория микромира, является то, что каждой симметрии соответствует свой закон сохранения. Например, симметрии относительно сдвигов во времени (то есть тому обстоятельству, что законы физики одинаковы в каждый момент времени) соответствует закон сохранения энергии, симметрии относительно сдвигов в пространстве — закон сохранения импульса, а симметрии относительно поворотов в пространстве (все направления в пространстве равноправны) — закон сохранения углового момента. Законы сохранения можно интерпретировать и как запреты: перечисленные симметрии запрещают изменение энергии, изменение импульса и изменение углового момента замкнутой системы при ее эволюции. Каждому закону сохранения соответствует своя симметрия; это утверждение является точным в квантовой теории. Спрашивается, какая же симметрия соответствует закону сохранения электрического заряда? Ясно, что симметрии пространства и времени здесь ни при чем. Тем не менее, необходимая симметрия имеется. Дело в том, что помимо очевидных пространственно-временных симметрий существуют неочевидные, «внутренние» симметрии. Одна из них и приводит к сохранению электрического заряда. Чтобы пояснить эту связь между наличием только двух типов поляризации света и отсутствием массы у фотона, напомним, что элементарные частицы характеризуются спином, который может быть полуцелым или целым (в единицах постоянной Планка). Элементарные фермионы (частицы с полуцелым спином) имеют спин 1/2. Это электрон e, электронное нейтрино ν e, тяжелые аналоги электрона — мюон μ и τ-лептон, их нейтрино νμ и ντ, кварки шести типов u, d, c, s, t, b и соответствующие всем им античастицы (позитрон e +, антинейтрино 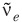 , антикварк ũ и т. д.). Кварки u и d — легкие, и из них состоят протон (кварковый состав uud) и нейтрон (udd). Остальные кварки — более тяжелые, они входят в состав короткоживущих частиц, например К -мезонов.
, антикварк ũ и т. д.). Кварки u и d — легкие, и из них состоят протон (кварковый состав uud) и нейтрон (udd). Остальные кварки — более тяжелые, они входят в состав короткоживущих частиц, например К -мезонов.
Частицы с целым спином называют бозонами. К ним относится фотон, он имеет спин 1. Единичным спином обладают и глюоны — отдаленные аналоги фотона, отвечающие за взаимодействия между кварками и связывающие их в протон, нейтрон и другие составные частицы. Кроме того, есть еще три частицы с единичным спином — электрически заряженные W + W –-бозоны и нейтральный Z -бозон. О них еще пойдет речь впереди. Ну а частица Хиггса должна иметь нулевой спин.
Заметим, кстати, что мы только что перечислили все элементарные частицы, имеющиеся в Стандартной модели.
|
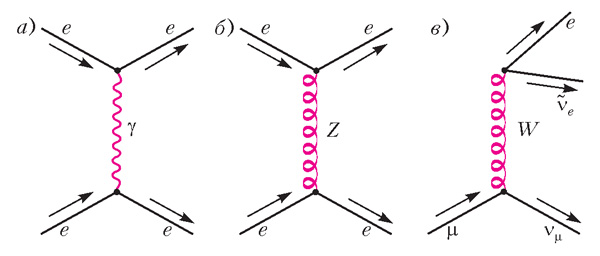
Массивная частица со спином s (в единицах ħ) имеет (2 s + 1) состояний с разными проекциями спина на заданную ось (спин — это вектор, так что понятие его проекции на заданную ось имеет обычный смысл). Например, спин электрона в его системе покоя может быть направлен вверх: sz = +1/2 или вниз: sz = –1/2. Бозон Z обладает ненулевой массой и спином s = 1, поэтому состояний с разными проекциями спина у него три: sz = +1, 0 или –1. Совершенно иначе обстоит дело с безмассовыми частицами. Поскольку они летают со скоростью света, перейти в систему отсчета, где такая частица покоится, нельзя. Тем не менее, можно говорить о проекции спина на направление движения. Так вот, несмотря на то что спин фотона равен единице, таких проекций может быть всего две — вдоль и против направления движения. Это и есть правая и левая поляризации фотона (света). Третье состояние с нулевой проекцией спина, которое обязано было бы существовать, будь у фотона масса, запрещено глубокой внутренней симметрией электродинамики, той самой симметрией, что приводит к сохранению электрического заряда. Ключевыми для нас являются, однако, не фотоны, a W ±- и Z -бозоны. Эти частицы, открытые в 1983 году и задолго до этого предсказанные теоретиками, обладают спином 1 и довольно большой массой: W ±-бозоны имеют массу 80 ГэВ (то есть они примерно в 80 раз тяжелее протона), а Z -бозон имеет массу 91 ГэВ. Свойства W ±- и Z -бозонов сейчас хорошо известны, в основном благодаря экспериментам на электрон-позитронном и протон-антипротонном коллайдерах: точность измерений целого ряда величин, относящихся к W ±- и Z -бозонам, лучше 0,1%. Эти свойства, как и свойства других частиц, прекрасно описываются Стандартной моделью. Последнее замечание относится и к взаимодействиям W ±- и Z -бозонов с электроном, нейтрино, кварками и другими частицами. Эти взаимодействия, кстати, называют слабыми. Они изучены во всех деталях; один из давно известных примеров их проявления — это β-распады мюона, нейтрона и ядер.
|
Каждый из W ±- и Z -бозонов может находиться в трех спиновых состояниях, а не в двух, как фотон. Тем не менее, их взаимодействия с фермионами (нейтрино, кварками, электроном и т. д.) устроены в принципе так же, как взаимодействие фотона. Например, фотон взаимодействует с электрическим зарядом электрона и электрическим током, который создает движущийся электрон. Точно так же Z -бозон взаимодействует с некоторым зарядом электрона и током, возникающим при движении электрона, только эти заряд и ток не совпадают с электрическими. С точностью до важной особенности, о которой пойдет вскоре речь, аналогия будет полной, если помимо электрического заряда электрону приписать еще и z -заряд. Своими z -зарядами обладают и кварки, и нейтрино. Так же, как и теория фотона, теория W ±- и Z -бозонов обладает глубокой внутренней симметрией, близкой к той, что приводит к закону сохранения электрического заряда. В полной аналогии с фотоном, эта внутренняя симметрия запрещает W ± и Z -бозонам иметь третью поляризацию, а стало быть и массу.Симметрийный запрет на массу частицы со спином 1 действительно работает в случае фотона, а в случае W ±- и Z -бозонов этот запрет не работает. Слабые взаимодействия — взаимодействия электронов, нейтрино, кварков и других частиц с W ±- и Z -бозонами — устроены так, как если бы эти фермионы не имели никакой массы. Дело здесь не в числе поляризаций: и у массивных, и у безмассовых фермионов поляризаций (направлений спина) может быть ровно две.
Говоря о связи симметрии с законами сохранения и запретами, мы упустили из виду одно обстоятельство. Оно заключается в том, что законы сохранения и симметрийные запреты выполняются только тогда, когда симметрия присутствует явно. Однако симметрии могут быть и нарушенными. Например, в однородном образце железа при комнатной температуре всегда имеется магнитное поле, направленное в какую-то сторону; образец представляет собой магнит. Если бы существовали микроскопические существа, живущие внутри этого магнита, то они бы обнаружили, что не все направления пространства вокруг них равноправны: на электрон, летящий поперек магнитного поля, действует сила со стороны магнитного поля — сила Лоренца, а на электрон, летящий вдоль поля, сила не действует. Соответственно, движение электрона вдоль магнитного поля происходит по прямой, поперек поля — по окружности, а в общем случае — по спирали. Стало быть, магнитное поле внутри образца нарушает симметрию относительно вращений в пространстве. В связи с этим внутри магнита не выполняется и закон сохранения углового момента: при движении электрона по спирали проекция углового момента на ось, перпендикулярную магнитному полю, меняется со временем.
|
Здесь мы имеем дело со спонтанным нарушением симметрии. В отсутствие внешних воздействий (например, магнитного поля Земли) в разных образцах железа магнитное поле может быть направлено в разные стороны, и ни одно из этих направлений не будет предпочтительнее другого. Исходная симметрия относительно вращений по-прежнему имеется, и проявляется она в том, что магнитное поле в образце может быть направлено куда угодно. Но раз уж магнитное поле возникло, появилось и выделенное направление, и симметрия внутри магнита оказалась нарушенной. На более формальном уровне: уравнения, управляющие взаимодействием атомов железа между собой и с магнитным полем, симметричны относительно вращений в пространстве, но состояние системы этих атомов — образца железа — несимметрично. В этом и состоит явление спонтанного нарушения симметрии. Отметим, что мы здесь говорим о наиболее выгодном состоянии, имеющем наименьшую энергию; такое состояние называют основным. Именно в нем окажется в конце концов образец железа, даже если изначально он был ненамагниченным.
Итак, спонтанное нарушение некоторой симметрии имеет место тогда, когда уравнения теории симметричны, а основное состояние — нет. Слово «спонтанное» употребляют в этом случае в связи с тем, что система сама, без нашего участия, выбирает несимметричное состояние, поскольку именно оно является энергетически наиболее выгодным. Из приведенного примера ясно, что если симметрия спонтанно нарушена, то вытекающие из нее законы сохранения и запреты не работают; в нашем примере это относится к сохранению углового момента. Подчеркнем, что полная симметрия теории может быть нарушена лишь частично: в нашем примере из полной симметрии относительно всех вращений в пространстве остается ненарушенной симметрия относительно вращений вокруг направления магнитного поля.
|
Заключение
С «технической» точки зрения, Стандартая модель внутренне непротиворечива. Это означает, что в ее рамках можно — хотя бы в принципе, а как правило и на практике — вычислить любую физическую величину (разумеется, относящуюся к тем явлениям, которые призвана описывать Стандартная модель) и результат не будет содержать неопределенностей. Тем не менее, многие, хотя и не все, теоретики считают положение дел в Стандартной модели не вполне удовлетворительным, мягко говоря. И связано это в первую очередь с ее энергетическим масштабом.
Как ясно из предыдущего, энергетический масштаб Стандартной модели имеет порядок М с.м. = 100 ГэВ (мы здесь не говорим о сильных взаимодействиях с масштабом 1 ГэВ, с этим масштабом всё проще). Это масштаб масс W ±- и Z -бозонов и бозона Хиггса. Много это или мало? С экспериментальной точки зрения — немало, а вот с теоретической...
В физике имеется еще один масштаб энергий. Он связан с гравитацией и равен планковской массе MP = 1019 ГэВ. При низких энергиях гравитационные взаимодействия между частицами пренебрежимо слабы, но они усиливаются с ростом энергии, и при энергиях порядка MP гравитация становится сильной. Область энергий выше MP — это область квантовой гравитации, что бы она из себя ни представляла. Для нас важно, что гравитация — самое, пожалуй, фундаментальное взаимодействие, и гравитационный масштаб MP — самый фундаментальный масштаб энергий. Почему же тогда масштаб Стандартной модели так далек от гравитационного масштаба?
У обозначенной проблемы есть еще один, более тонкий аспект. Он связан со свойствами физического вакуума. В квантовой теории вакуум — основное состояние природы — устроен совсем нетривиально. В нем всё время рождаются и уничтожаются виртуальные частицы, иными словами, образуются и исчезают флуктуации полей. Непосредственно наблюдать эти процессы мы не можем, но они оказывают влияние на наблюдаемые свойства элементарных частиц, атомов и т. д. Например, взаимодействие электрона в атоме с виртуальными электронами и фотонами приводит к наблюдаемому в атомных спектрах явлению — лэмбовскому сдвигу. Другой пример — поправка к магнитному моменту электрона или мюона (аномальный магнитный момент) тоже обусловлена взаимодействием с виртуальными частицами. Эти и подобные эффекты вычислены и измерены (в указанных случаях с фантастической точностью!), так что мы можем быть уверены, что имеем правильную картину физического вакуума.
В этой картине все параметры, изначально закладываемые в теорию, получают поправки, связанные с взаимодействием с виртуальными частицами. Их называют радиационными поправками. В квантовой электродинамике эти поправки малы, а вот в теории Энглера–Браута–Хиггса они огромны. Такова особенность элементарных скалярных полей; у других полей этого свойства нет. Главный эффект здесь состоит в том, что радиационные поправки стремятся «подтянуть» энергетический масштаб Стандартной модели к гравитационному масштабу. Если оставаться в рамках Стандартной модели, то единственный выход — подобрать изначальные параметры теории так, чтобы вместе с радиационными поправками они приводили к правильному значению М с.м.. При этом выясняется, что точность подгонки должна составлять величину, близкую к отношению М с.м.2/ MP 2 = 10–34! В этом и состоит второй аспект проблемы энергетического масштаба Стандартной модели: представляется неправдоподобным, что такая подгонка имеет место в природе.
Многие (хотя, повторим, не все) теоретики считают, что эта проблема однозначно свидетельствует о необходимости выхода за рамки Стандартной модели. Действительно, если Стандартная модель перестает работать или существенно расширяется на энергетическом масштабе новой физики М н.ф., то аргумент о радиационных поправках модифицируется. Требуемая точность подгонки параметров в этом случае составляет, грубо говоря, М с.м.2/ М н.ф.2, а на самом деле на пару порядков слабее. Если считать, что тонкой подстройки параметров в природе нет, то отсюда следует, что масштаб «новой физики» должен лежать в области 1–2 ТэВ, то есть как раз в области, доступной для исследования на Большом адронном коллайдере!
Какой могла бы быть «новая физика»? Единства у теоретиков по этому поводу нет. Один вариант — составная природа скалярных полей, обеспечивающих спонтанное нарушение симметрии. О нем мы уже говорили. Другая, тоже популярная (пока?) возможность — суперсимметрия. На ней мы останавливаться не будем; скажем только, что суперсимметрия предсказывает целый зоопарк новых частиц с массами в области сотен ГэВ — нескольких ТэВ. Обсуждаются и весьма экзотические варианты вроде дополнительных измерений пространства.
Несмотря на все усилия, до сих пор никаких экспериментальных указаний на «новую физику» получено не было. Это, вообще-то, уже начинает внушать тревогу: а правильно ли мы всё понимаем? Вполне возможно, впрочем, что мы еще не добрались до «новой физики» по энергии и по количеству набранных данных и что именно с ней будут связаны новые, революционные открытия. Основные надежды здесь возлагаются опять-таки на Большой адронный коллайдер, который через полтора года начнет работать на полную энергию 13–14 ТэВ и быстро набирать данные.
Литература
1. Хиггса механизм — статья в Физической энциклопедии в 5 тт., том 5, М.: БРЭ, 1999
2. А. И. Вайнштейн, В. И. Захаров, М. А. Шифман. Хиггсовские частицы // УФН. — 1980. — Т. 131. — № 8.
3. Ансельм А. А., Уральцев Н. Г., Хозе В. А. «Хиггсовские частицы». УФН том 145, 185—223 (1985).
4. Богуш А. А. Введение в калибровочную полевую теорию электрослабых взаимодействий. — 2-e изд. — УРСС, 2003. — ISBN 5-354-00436-5
5. Рубаков В. А. Классические калибровочные поля: Бозонные теории. Изд 3-е. — М.: УРСС, 2010
6. Рубаков В. А. Классические калибровочные поля: Теории с фермионами. Некоммутативные теории. Изд 3-е. — М.: УРСС, 2009
7. Вайнберг С. Квантовая теория поля. — М.: Физматлит, 2003. — Т. 1, 2.
Date: 2015-05-19; view: 822; Нарушение авторских прав

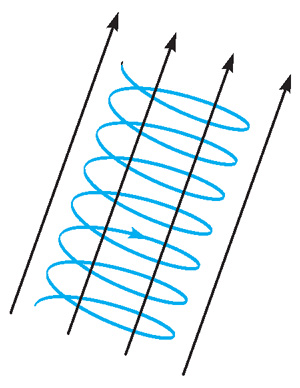 Движение электрона по спирали в магнитном поле
Движение электрона по спирали в магнитном поле
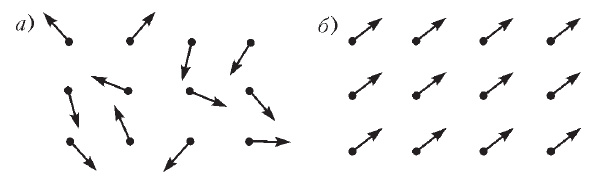 Спонтанное нарушение симметрии в образце железа в присутствии магнитного поля
Спонтанное нарушение симметрии в образце железа в присутствии магнитного поля