Уравнение Шредингера. Одномерное уравнение Шредингера. Стационарное уравнение Шредингера

Рассмотрим важный частный случай независящего от времени гамильтониана: .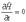

В этом случае существуют специальные решения уравнения Шрёдингера, которые легко получаются методом разделения переменных:

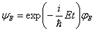, где 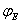не зависят от времени и являются (как и 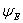) собственными векторами гамильтониана: .

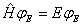Собственные значения 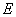являются допустимыми значениями энергии системы, так как гамильтониан – оператор энергии, соответствующий классической функции Гамильтона. Состояния 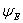называются стационарными состояниями. Их основные свойства таковы:

1) плотность вероятности и поток вероятности в этих состояниях не зависят от времени: .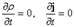

2) Средние значения наблюдаемых не зависят от времени: при .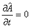

3) Вероятность обнаружить собственное значение 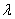наблюдаемой 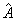не зависит от времени:

.

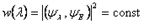Произвольное (нестационарное) состояние может быть разложено по стационарным состояниям – собственным векторам гамильтониана:

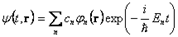. В нестационарном состоянии энергия не имеет определенного значения, но среднее значение ее от времени не зависит:

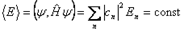, так как - интеграл движения: .
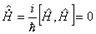Если наблюдаемая 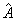не коммутирует с гамильтонианом, то ее среднее, как и должно быть, зависит от времени (даже при 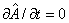): 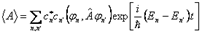.Присутствие здесь недиагональных матричных элементов оператора наблюдаемой 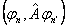отражает характерный квантовомеханический эффект интерференции различных стационарных состояний. Легко проверить, что в нестационарном состояни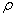и и 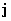также зависят от времени.