Теорема Умова— Пойнтинга для мгновенных значений

Кроме уравнений Максвелла, большое значение в теории электромагнитного поля имеет теорема Умова—Пойнтинга, которая описывает энергетические соотношения в поле.

Теорема Умова—Пойнтинга имеет две формы записи: первая — для мгновенных значений, вторая — комплексная форма — для синусоидально изменяющихся величин.

Известно, что энергия электрического поля в единице объема равна 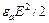. Энергия магнитного поля в единице объема 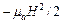. Энергия в объеме 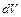равна .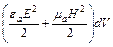

Для того чтобы образовать выражение, в которое вошла бы полная энергия в объеме 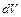, умножим первое уравнение Максвелла на 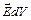, а второе на 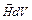. Получим

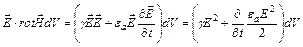
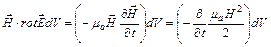
Из первого выражения вычтем второе. Тогда

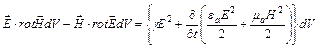
Так как 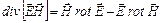, то левая часть полученного выражения есть 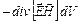. Следовательно,

.

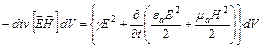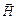Для сокращения записи обозначим векторное произведение на через 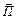, т. е. примем, что 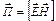; 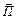— это вектор, называемый вектором Пойнтинга; размерность его равна произведению размерносте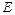й и :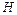

.

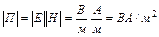Таким образом, вектор Пойнтинга имеет размерность мощности (или энергии в единицу времени), отнесенной к единице поверхности, и направление его (рис. 7.2) совпадает с направлением движения острия правого винта, если головку последнего вращать по кратчайшему направлению от к 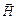. Следовательно,

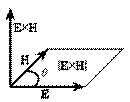
Рис. 7.2. Вектор Пойнтинга

Распространим данное выражение на некоторый объем конечных размеров. С этой целью проинтегрируем выражение по объему :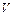

Подобно тому, как поверхностный интеграл по теореме Стокса преобразовывается в линейный: ,объемный интеграл в свою очередь может быть преобразован в поверхностный. Это преобразование осуществляют с помощью теоремы Остроградского—Гаусса .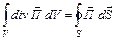

Теорему Умова—Пойнтинга для мгновенных значений записывают следующим образом:

.

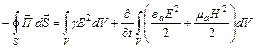Левая часть выражения представляет собой поток вектора Пойнтинга (направленный внутрь объема) сквозь любую замкнутую поверхность 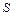, ограничивающую некоторый объем .

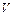В соответствии с уравнением Джоуля—Ленца в дифференциальной форме — энергия, выделяющаяся в виде теплоты в единице объема в единицу времени.

Поэтому есть энергия, выделяющаяся в виде теплоты в единицу времени в объеме 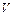; 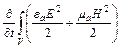есть скорость изменения запаса электромагнитной энергии в единице объема.

Но скорость изменения электромагнитной энергии есть мощность. Следовательно, поток вектора Пойнтинга сквозь любую замкнутую поверхность, ограничивающую объем 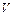, равен мощности, выделяющейся в объеме 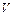в виде теплоты, и мощности, идущей на приращение энергии электромагнитного поля.

Теорему Умова—Пойнтинга следует трактовать как уравнение энергетического баланса; левая часть есть мощность или энергия в единицу времени, доставляемая в виде потока вектора Пойнтинга внутрь некоторого объема; правая часть есть энергия, расходуемая в единицу времени внутри объема.

Теорема Умова—Пойнтинга для мгновенных значений была получена в предположении, что среда внутри объема 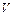однородна и изотропна, а также в предположении, что отсутствует отраженная волна и внутри объема нет источников электродвижущей силы.

Если поле не изменяется во времени, то

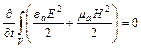и .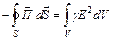

Обратим внимание также на то, что теорема учитывает возможность прохождения потока вектора 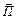транзитом через объем .

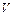Электромагнитная энергия от места ее генерирования передается к месту потребления по диэлектрику (провода же в линиях передачи выполняют двоякую роль: они являются каналами, по которым проходит ток, и организаторами структуры поля в диэлектрике).

Date: 2015-05-18; view: 815; Нарушение авторских прав