
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 5. Колебательное движение материальной точки
|
|
I: 161.
S: На двух одинаковых лёгких спиральных пружинках подвешены две гири, отношение масс которых m 1/ m 2 = 4. Гири получили толчки в вертикальном направлении и колеблются с одинаковыми амплитудами. Как относится: а) периоды их колебаний Т 1/ Т 2 ? б) энергии колебаний Е 1/ Е 2 ? Т 1/ Т 2 = …; Е 1/ Е 2 = …
+: 2*1.
I: 162.
S: Дифференциальное уравнение движения материальной точки имеет вид
3ּ d 2 x/dt 2 + 12ּ dx/dt + c ּ x = 0.
Определить максимальное значение коэффициента жёсткости С пружины, при котором движение будет апериодическим; с = …
Отметьте правильный ответ.
+: 12
I: 163.
S: Дифференциальное уравнение колебательного движения материальной точки дано в виде
d 2 x/dt 2 + 50ּ x = 25ּ sin (5 ּt).
Определить амплитуду А вынужд вынужденных колебаний; А вынужд = …
+: 1
I: 164.
S: Дифференциальное уравнение движения материальной точки имеет вид
d 2 x/dt 2 + 2ּ dx/dt + 100ּ x = 15ּ sin 8 ּt.
(Расстояние в метрах.) Определить амплитуду вынужденных колебаний А вынужд;(результат вычисления округлить с точностью до первого знака после запятой);
А вынужд = ….
+: 0,4
I: 165.
S: Тело массой m = 2 кг движется прямолинейно по закону x = 10ּ sin (2 ּt) (м) под действием силы F. Определить наибольшее значение этой силы;
| F | = …(H).
+: 80
I: 166.
S: Тело, подвешенное к пружине с коэффициентом жёсткости с = 800 Н/м, совершает свободные вертикальные колебания с амплитудой 0,2 м. Колебания начались из положения статического равновесия с начальной скоростью 4 м/с. Определить массу m тела (результат вычисления округлить до целого числа);
m = … (кг).
+: 2
I: 167.
S: Груз массой m = 3 кг подвешен к пружине с коэффициентом жёсткости с = 300 Н/м и находится в свободном вертикальном колебательном движении. В начальный момент времени его скорость v 0 = 2 м/с, а смещение от положения статического равновесия х 0 = 0,15 м. Определить амплитуду А колебаний груза (результат вычисления округлить до второго знака после запятой включительно). А = … (м).
+: 0,25
I: 168.
S: Материальная точка с массой 0,2 кг совершает колебания по закону
s = 0,08 · (20 ·π·t + π /4) (м). Найти полную энергию Е (сумму кинетической и потенциальной энергий) матер. точки. Результат вычисления округлить до первого знака после запятой включительно. Е = … (Дж).
+: 2,5
I: 169.
S: Маятниковые часы идут на поверхности Земли точно. На сколько |Δ t | (сек.) они отстанут за одни сутки, если их поднять на сотый этаж высотного дома? Высота этажа 3 м. Радиус Земли принять равным R. = 6400 км. Результат вычисления округлить до целого числа. |Δ t | = … (сек).
+: 4.
I: 170.
S: Дифференциальное уравнение движения материальной точки имеет вид
m ּ d 2 x/dt 2 + 4ּ dx/dt + 2ּ x = 0.
Определить максимальное значение массы m max точки, при котором движение будет апериодическим: m max = …
+: 2
I: 171.
S: Дифференциальное уравнение движения материальной точки имеет вид
d 2 x/dt 2 + 5ּ dx/dt + 5ּ x = 0.
Определить, каким будет движение: равномерным, равноускоренным, колебательным или апериодическим.
Отметьте правильный ответ.
-: Равномерное; -: Равноускоренное; -: Колебательное; +: Апериодическое
I: 172.
S: Дифференциальное уравнение движения материальной точки имеет вид
d 2 x/dt 2 + 2ּ dx/dt + 2ּ x = 0.
Определить, каким будет движение: равномерным, равноускоренным, колебательным или апериодическим.
Отметьте правильный ответ.
-: Равномерное; -: Равноускоренное; +: Колебательное; -: Апериодическое
I: 173.
S: Груз массой m = 2 кг подвешен к пружине, коэффициентом жёсткости которой
С = 30 Н/м, и выведен из состояния равновесия. Сила сопротивления движению
R = - 0,4 ּv (Н). Определить, каким будет движение: равномерным, колебательным или апериодическим.
Отметьте правильный ответ.
-: Равномерное; +: Колебательное; -: Апериодическое.
I: 174.
S: Дифференциальное уравнение движения материальной точки имеет вид
5ּ d 2 x/dt 2 + 20ּ dx/dt + c ּ x = 0.
Определить наибольшее значение коэффициента жёсткости с пружины, при котором движение будет апериодическим; c = …
+: 20.
I: 175.
S: Груз массой m = 0,4 кг подвешен к пружине и совершает свободные колебания с амплитудой 0,4 м. Колебания начались из положения статического равновесия с начальной скоростью 3 м/с.
Определить коэффициент жёсткости пружины (результат вычисления округлить до первого знака после запятой включительно); c = … (Н/м).
+: 22,5
I: 176.
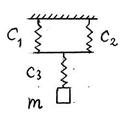 S: Коэффициент жёсткости пружин С 1 = С 2 = С 3 = 300 Н/м, масса груза m = 2 кг.
S: Коэффициент жёсткости пружин С 1 = С 2 = С 3 = 300 Н/м, масса груза m = 2 кг.
Определить циклическую частоту ω собственных вертикальных колебаний груза;
ω = … (1/сек)
+: 10
I: 177.
S: Какое уравнение описывает указанный процесс?
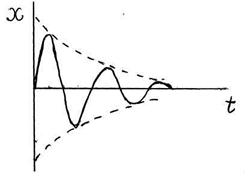
Отметьте правильный ответ.
-: d 2 x/dt 2 + k 2 ּx = sin pּt
+: d 2 x/dt 2 + 2ּnּdx/dt + k 2 ּx = 0
-: d 2 x/dt 2 + k 2 ּx = sin kּt
-: d 2 x/dt 2 + 2ּnּdx/dt + k 2 ּx = b
I: 178.
S: Какое уравнение описывает указанный процесс?
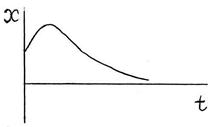
Отметьте правильный ответ.
-: d 2 x/dt 2 + k 2 ּx = 0, -: d 2 x/dt 2 + k 2ּ x = b,
-: d 2 x/dt 2 + k 2 ּx = sin kּt, +: d 2 x/dt 2 + 2ּnּdx/dt + k 2 ּx = 0.
I: 179.
S: Какое уравнение описывает указанный процесс?
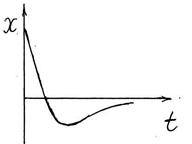
Отметьте правильный ответ.
-: d2x/dt2 + k 2ּx = 0
-: d 2 x/dt 2 + k 2 ּx = b
-: d 2 x/dt 2 + k 2 ּx = sin kּt
+: d 2 x/dt 2 + 2ּnּdx/dt + k 2 ּx = 0
I: 180.
S: Какое уравнение описывает указанный процесс?
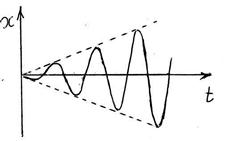
Отметьте правильный ответ.
-: d2x/dt2 + k 2ּx = 0
-: d 2 x/dt 2 + k 2 ּx = b
-: d 2 x/dt 2 + k 2 ּx = sin (pּt),
+: d 2 x/dt 2 + k 2 ּx = sin (kּt).
I: 181.
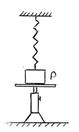 S: К пружине жёсткости k, один конец которой закреплён, подвешен груз веса Р, лежащий на подставке так, что пружина не растянута (см. рис.). Без толчка подставка убирается. Найти закон движения груза x (t).
S: К пружине жёсткости k, один конец которой закреплён, подвешен груз веса Р, лежащий на подставке так, что пружина не растянута (см. рис.). Без толчка подставка убирается. Найти закон движения груза x (t).
Отметьте правильный ответ.
-: x (t) = 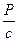 ּ cos (
ּ cos (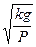 ּ t) +
ּ t) + 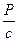 ּ sin (
ּ sin (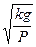 ּ t)
ּ t)
-: x (t) = 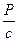 ּ cos (
ּ cos (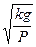 ּ t)
ּ t)
+: x (t) = 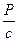 ּ[1 – cos (
ּ[1 – cos (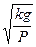 ּ t)]
ּ t)]
-: x (t) = 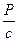 ּ[1 + sin (
ּ[1 + sin (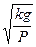 ּ t)]
ּ t)]
I: 182.
S: Длина маятника Фуко в Исаакиевском соборе в Петербурге 98 м. Определить период колебаний Т маятника (g = 9,8 м/с2). Результат вычисления округлить до ближайшего целого числа. Т = … (сек)
+: 20
I: 183.
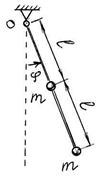 S: Маятник представляет собой шарнирно соединённую со штативом лёгкую жёсткую спицу с закреплёнными на ней двумя небольшими по размерам грузами массы m каждый (см. рис.). Расстояния между точкой крепления О и верхним грузом и между грузами равны l. Период колебаний имеет вид:
S: Маятник представляет собой шарнирно соединённую со штативом лёгкую жёсткую спицу с закреплёнными на ней двумя небольшими по размерам грузами массы m каждый (см. рис.). Расстояния между точкой крепления О и верхним грузом и между грузами равны l. Период колебаний имеет вид:
Т = 2 ּπּQּ 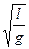
(g – ускорение свободного падения). Определить Q. (Результат вычисления округлить до второго знака после запятой включительно.) Q = …
+: 1,29
I: 184.
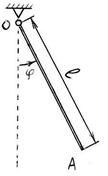 S: Определить период Т малых свободных колебаний в вертикальной плоскости маятника, представляющего собой шарнирно соединённый со штативом тонкий однородный стержень массы m длины l.
S: Определить период Т малых свободных колебаний в вертикальной плоскости маятника, представляющего собой шарнирно соединённый со штативом тонкий однородный стержень массы m длины l.
Искомый период колебаний имеет вид:
Т = 2 ּπּQּ 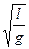
(g – ускорение свободного падения; момент инерции стержня ОА относительно шарнира О: J О = (1/3) ·m·l 2 ). Определить Q. (Результат вычисления округлить до второго знака после запятой включительно.) Q = …
+: 0,82
I: 185.
 S: Тело массы m = 0,5 кг совершает колебания на пружине так, что наибольшее значение скорости v макс = 100 см/сек, наибольшее отклонение от положения равновесия x макс = 5 см Определить коэффициент жёсткости c пружины,
S: Тело массы m = 0,5 кг совершает колебания на пружине так, что наибольшее значение скорости v макс = 100 см/сек, наибольшее отклонение от положения равновесия x макс = 5 см Определить коэффициент жёсткости c пружины,
с = … (Н/м).
+: 200
I: 186.
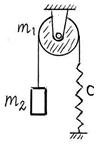 S: Через неподвижный блок с массой m 1 = 260 г перекинута нить, к концу которой подвешен груз массы m 2 = 330 г. Другой конец нити привязан к пружинке с закреплённым нижним концом (см. рис.). Коэффициент жёсткости пружины c = 500 (Н/м). Вычислить период колебаний груза. Нить не может скользить по поверхности блока; блок однородный цилиндр; трение в оси блока отсутствует. (Результат вычисления округлить до первого знака после запятой включительно.)
S: Через неподвижный блок с массой m 1 = 260 г перекинута нить, к концу которой подвешен груз массы m 2 = 330 г. Другой конец нити привязан к пружинке с закреплённым нижним концом (см. рис.). Коэффициент жёсткости пружины c = 500 (Н/м). Вычислить период колебаний груза. Нить не может скользить по поверхности блока; блок однородный цилиндр; трение в оси блока отсутствует. (Результат вычисления округлить до первого знака после запятой включительно.)
Т = … (сек.).
+: 0,2
I: 187.
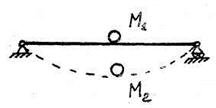 S: Груз М поместили без начальной скорости к середине неизогнутой балки жёсткости с = 400 Н/см. Балка совершает поперечные колебания с амплитудой A = 3 см. Определить период колебаний балки (g = 9,81 м/с2). (Результат вычисления округлить до второго знака после запятой включительно.) Т = … (сек).
S: Груз М поместили без начальной скорости к середине неизогнутой балки жёсткости с = 400 Н/см. Балка совершает поперечные колебания с амплитудой A = 3 см. Определить период колебаний балки (g = 9,81 м/с2). (Результат вычисления округлить до второго знака после запятой включительно.) Т = … (сек).
+: 0,35
I: 188.
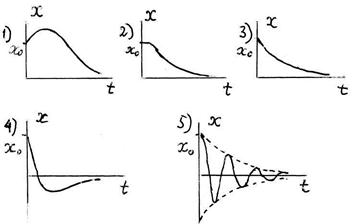
S: Тело массы m, подвешенное па пружине жёсткости с, находится в состоянии статического равновесия в среде с сопротивлением. Сила сопротивления пропорциональна первой степени скорости, | F сопр| = bּv. Коэффициент сопротивления b равняется 0,5ּ 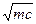 . Тело отклонили от положения равновесия на расстояние на расстояние x 0 (x 0 > 0) и отпустили без начальной скорости.
. Тело отклонили от положения равновесия на расстояние на расстояние x 0 (x 0 > 0) и отпустили без начальной скорости.
Определить закон движения тела.
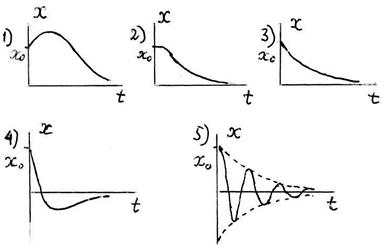
Отметьте правильный ответ.
-: 1); -: 2); -: 3); -: 4); +: 5)
I: 189.
S: Тело массы m, подвешенное на пружине жёсткости с, находится в состоянии статического равновесия в среде с сопротивлением. Сила сопротивления пропорциональна первой степени скорости, | F сопр| = bּv.
Коэффициент сопротивления b равняется b = 2ּ 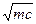 .
.
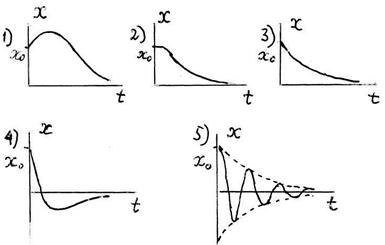 Тело отклонили от положения равновесия на расстояние x 0 (x 0 > 0) и отпустили без начальной скорости.
Тело отклонили от положения равновесия на расстояние x 0 (x 0 > 0) и отпустили без начальной скорости.
Определить закон движения тела.
Отметьте правильный ответ.
-: 1); +: 2); -: 3); -: 4); -: 5)
I: 190.
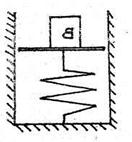 S: Груз В весом Р = 200 Н положен без начальной скорости на невесомую плиту, прикреплённую к вертикальной пружине. После этого груз стал совершать гармонические колебания с амплитудой A = 5 см. Определить период малых колебаний груза (g = 9,81 м/с2). (Результат вычисления округлить до второго знака после запятой включительно.)
S: Груз В весом Р = 200 Н положен без начальной скорости на невесомую плиту, прикреплённую к вертикальной пружине. После этого груз стал совершать гармонические колебания с амплитудой A = 5 см. Определить период малых колебаний груза (g = 9,81 м/с2). (Результат вычисления округлить до второго знака после запятой включительно.)
Т = … (сек.).
+: 0,45
I: 191.
S: Груз массы m = 1 кг подвешен на пружине, с коэффициентом жёсткости с = 625 Н/м. На груз действует вынуждающая сила F вынужд = 5ּ cos (ωt) + 2ּcos (5 ωt) (Н). Определить, при каких значениях ω 1 и ω 2 наступит резонанс (ω 1 > ω 2).
1) ω 1 = … (рад/сек), 2) ω 2 = … (рад/сек).
+: 25*5
I: 192.
S: Тело массы m, подвешенное на пружине жёсткости с, находится в состоянии статического равновесия в среде с сопротивлением. Сила сопротивления пропорциональна первой степени скорости, | F сопр| = bּv. Коэффициент сопротивления b равняется b = 2ּ 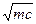 .
.
Тело отклонили от положения равновесия на расстояние x 0 (x 0 > 0) и сообщили ему начальную скорость, направленную в сторону первоначального отклонения (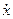 0 >
0 >  0). Определить закон движения тела.
0). Определить закон движения тела.
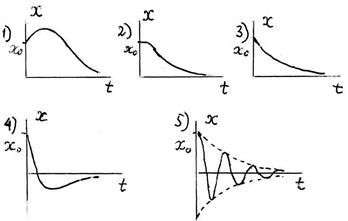
Отметьте правильный ответ.
+: 1); -: 2); -: 3); -: 4); -: 5)
I: 193.
S: Тело массы m = 0,25 кг, подвешенное на пружине жёсткости с = 144 Н/м, находится в состоянии статического равновесия в среде с сопротивлением. Сила сопротивления пропорциональна первой степени скорости, | F сопр| = bּv. Коэффициент сопротивления b равняется b = 12 (Нּс/м).
Тело отклонили от положения равновесия на расстояние x 0 = 0,2 м и сообщили ему начальную скорость, направленную в противоположную сторону, 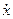 0 = – 2 м/с. Определить закон движения тела.
0 = – 2 м/с. Определить закон движения тела.
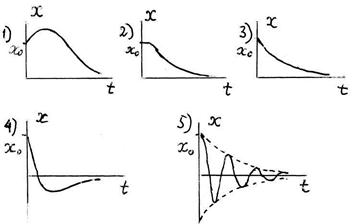
Отметьте правильный ответ.
-: 1); -: 2); +: 3); -: 4); -: 5)
I: 194.
S: Тело массы m = 0,25 кг, подвешенное на пружине жёсткости с = 144 Н/м, находится в состоянии статического равновесия в среде с сопротивлением. Сила сопротивления пропорциональна первой степени скорости, | F сопр| = bּv. Коэффициент сопротивления равняется b = 12 (Нּс/м).
Тело отклонили от положения равновесия на расстояние x 0 = 0,1 м и сообщили ему начальную скорость, направленную в противоположную сторону, 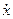 0 = – 3 м/с. Определить закон движения тела.
0 = – 3 м/с. Определить закон движения тела.
Отметьте правильный ответ.
-: 1); -: 2); -: 3); +: 4); -: 5)
I: 195.
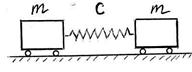 S: Два одинаковых груза массы m связаны пружиной (см. рис.). Частота колебаний оказалась равной ω 1. Затем один их грузов закрепили; частота собственных колебаний оказалась равной ω 2. Определить отношение ω 1/ ω 2. (Результат вычисления округлить до первого знака после запятой включительно.) ω 1/ ω 2 = …
S: Два одинаковых груза массы m связаны пружиной (см. рис.). Частота колебаний оказалась равной ω 1. Затем один их грузов закрепили; частота собственных колебаний оказалась равной ω 2. Определить отношение ω 1/ ω 2. (Результат вычисления округлить до первого знака после запятой включительно.) ω 1/ ω 2 = …
+: 1,4
I: 196.
S: Период колебаний маятника, точка подвеса которого покоится относительно земной поверхности, равен Т 0 =1,50 сек. Каков будет его период колебаний Т 1, если поместить маятник а вагон, движущийся горизонтально с ускорением а = 4,9 м/с2? Ускорение свободного падения принять равным g = 9,8 м/с2. Результат вычисления округлить до первого знака после запятой включительно. Т 1 = … (сек.).
+: 1,4.
I: 197.
S: Масса Луны в 81 раз меньше массы Земли, а радиус Земли в 3,7 раза больше радиуса Луны. Во сколько раз период колебаний маятника возрастёт при перенесении его с Земли на Луну? (Результат вычисления округлить до первого знака после запятой включительно.) τ 2/ τ 1 = …
+: 2,4
I: 198
S: При какой скорости поезда маятник длиной l = 11 см, подвешенный в вагоне, особенно сильно раскачивается, если длина рельсов 12,5 м? Ускорение свободного падения принять равным g = 9,8 м/с2). (Результат вычисления округлить до первого знака после запятой включительно.) v = … (м/сек.).
+: 18,8
I: 199.
S: Один из маятников за некоторое время совершил n 1 = 15 колебаний. Другой за то же время совершил n 2 = 14 колебаний. Разность длин маятников Δ l = 2,9 см. Найти длину l 1 первого маятника. (Результат вычисления округлить до первого знака после запятой включительно.) l 1 = … (см).
+: 19,6
I: 200.
S: Груз, подвешенный к пружине, вызвал удлинение её на Δ l = 4 см. Определить период Т собственных колебаний пружинного маятника. (g = 9,8 м/с2) (Результат вычисления округлить до первого знака после запятой включительно.) Т = … (сек.)
+: 0,4
Тема 6. Теорема о движении центра масс. Количество движения и кинетический момент механической системы. Теорема об изменении количества движения. Теорема об изменении кинетического момента.
I: 201.
S: Человек массы m = 60 кг переходит с носа на корму лодки. На какое расстояние по величине | s |переместится лодка длины l = 3 м, если её масса M = 120 кг?
| s | = … (м).
+: 1.
I: 202.
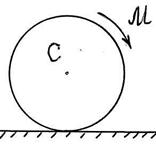 S: Колесо радиуса R = 0,5 м и массы m = 10 кг катится со скольжением по горизонтальной прямой под действием приложенного к нему вращательного момента M = 6 Нּм. Определить ускорение a C центра масс C колеса, если коэффициент трения скольжения равен f = 0,1. Ускорение свободного падения принять равным g = 10 м/с2. a C = …
S: Колесо радиуса R = 0,5 м и массы m = 10 кг катится со скольжением по горизонтальной прямой под действием приложенного к нему вращательного момента M = 6 Нּм. Определить ускорение a C центра масс C колеса, если коэффициент трения скольжения равен f = 0,1. Ускорение свободного падения принять равным g = 10 м/с2. a C = …
+: 1
I: 203.
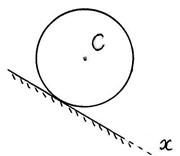 S: Колесо радиуса R = 0,5 м и массы m = 10 кг скатывается с наклонной плоскости вниз. Его центр масс C движется по закону x C = t 2 (м). Определить модуль главного вектора внешних сил | F(e) |, действующих на колесо; | F(e) | = … (Н).
S: Колесо радиуса R = 0,5 м и массы m = 10 кг скатывается с наклонной плоскости вниз. Его центр масс C движется по закону x C = t 2 (м). Определить модуль главного вектора внешних сил | F(e) |, действующих на колесо; | F(e) | = … (Н).
+: 20
I: 204.
S: Тело массы m = 40 г, брошенное вертикально вверх с начальной скоростью v 0 = 30 м/с, достигло высшей тоски спустя время t = 2,5 сек. Найти среднюю силу сопротивления F сопр. воздуха, действовавшую на тело во время движения. (Результат вычисления округлить до третьего знака после запятой включительно.) (g = 9,81 м/с2) F сопр. = … (Н)
+: 0,088
I: 205.
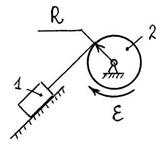 S: Тело 1 массой m = 50 кг поднимается по наклонной плоскости с помощью троса, намотанного на барабан 2 радиуса R = 0,4 м. Угловое ускорение барабана ε = 5 рад/с2. Определить модуль вектора всех внешних сил вектора внешних сил | F (e) |, действующих на тело;
S: Тело 1 массой m = 50 кг поднимается по наклонной плоскости с помощью троса, намотанного на барабан 2 радиуса R = 0,4 м. Угловое ускорение барабана ε = 5 рад/с2. Определить модуль вектора всех внешних сил вектора внешних сил | F (e) |, действующих на тело;
| F (e) | = … (Н).
+: 100
I: 206.
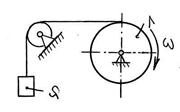 S: Шкив 1 массы М = 20 кг и радиуса R = 0,4 м, вращаясь с угловой скоростью ω = 2,5 рад/с, поднимает груз 2 массы m = 10 кг. Определить модуль количества движения | Q | механизма; | Q | = … (кгּм/с).
S: Шкив 1 массы М = 20 кг и радиуса R = 0,4 м, вращаясь с угловой скоростью ω = 2,5 рад/с, поднимает груз 2 массы m = 10 кг. Определить модуль количества движения | Q | механизма; | Q | = … (кгּм/с).
+: 10
I: 207.
S: Мяч массы m = 150 г ударяется о гладкую стенку под углом α = 30о к ней и отскакивает без потери скорости. Найти среднюю силу F, действующую на мяч со стороны стенки, если скорость мяча v 0 = 10 м/с, а продолжительность удара Δ t = 0,1 сек. F = … (Н).
+: 15
I: 208.
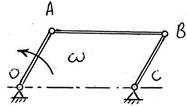 S: Масса каждого из тёх звеньев шарнирного параллелограмма ОАВС (ОА, АВ, СВ) равна 3 кг. Длина кривошипа ОА равна 0,6 м. Кривошип ОА вращается равномерно с угловой скоростью ω = 5 рад/с.
S: Масса каждого из тёх звеньев шарнирного параллелограмма ОАВС (ОА, АВ, СВ) равна 3 кг. Длина кривошипа ОА равна 0,6 м. Кривошип ОА вращается равномерно с угловой скоростью ω = 5 рад/с.
Определить модуль количества движения | Q | механизма; | Q | = … (кгּм/с).
+: 18
I: 209.
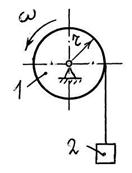 S: Цилиндр 1 вращается с угловой скоростью ω = 20 рад/с. Его момент инерции относительно оси вращения Ј = 2 кгּм2, радиус r = 0,5 м. Груз 2 имеет массу m 2 = 1 кг.
S: Цилиндр 1 вращается с угловой скоростью ω = 20 рад/с. Его момент инерции относительно оси вращения Ј = 2 кгּм2, радиус r = 0,5 м. Груз 2 имеет массу m 2 = 1 кг.
Определить модуль количества движения | Q | механизма; | Q | = … (кгּм/с).
+: 10
I: 210.
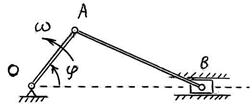 S: В кривошипно-шатунном механизме ОАВ, расположенном в горизонтальной плоскости, кривошип ОА и шатун АВ имеют каждый массу m = 3 кг, а ползун В имеет массу m /2 = 1,5 кг. Длина кривошипа OA l = 0,6 м, длина шатуна AB 2ּ l = 1,2 м. Угловая скорость кривошипа равна ω = 5 рад/с.
S: В кривошипно-шатунном механизме ОАВ, расположенном в горизонтальной плоскости, кривошип ОА и шатун АВ имеют каждый массу m = 3 кг, а ползун В имеет массу m /2 = 1,5 кг. Длина кривошипа OA l = 0,6 м, длина шатуна AB 2ּ l = 1,2 м. Угловая скорость кривошипа равна ω = 5 рад/с.
Определить модуль количества движения | Q | механизма в тот момент, когда угол α = π /2;
| Q | = … (кгּм/с).
+: 18
I: 211.
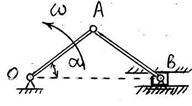 S: В кривошипно-шатунном механизме ОАВ, расположенном в горизонтальной плоскости, кривошип ОА и шатун АВ имеют каждый массу m = 3 кг и длину l = 0,6 м, а ползун В имеет массу m /2 = 1,5 кг. Угловая скорость кривошипа равна ω = 5 рад/с.
S: В кривошипно-шатунном механизме ОАВ, расположенном в горизонтальной плоскости, кривошип ОА и шатун АВ имеют каждый массу m = 3 кг и длину l = 0,6 м, а ползун В имеет массу m /2 = 1,5 кг. Угловая скорость кривошипа равна ω = 5 рад/с.
Определить модуль количества движения | Q | механизма в тот момент, когда угол α = 0;
| Q | = … (кгּм/с).
+: 9
I: 212.
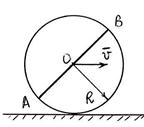 S: Сплошной однородный диск радиуса R = 0,5 м и массы m = 6 кг жёстко скрепленный с прямолинейным стержнем АВ тоже массы m и длиной 2ּ R, катится прямолинейно по гладкой поверхности так, что центр О имеет скорость v 0 = 5 м/с.
S: Сплошной однородный диск радиуса R = 0,5 м и массы m = 6 кг жёстко скрепленный с прямолинейным стержнем АВ тоже массы m и длиной 2ּ R, катится прямолинейно по гладкой поверхности так, что центр О имеет скорость v 0 = 5 м/с.
Определить модуль количества движения | Q | механизма;
| Q | = … (кгּм/с).
+: 60
I: 213.
S: Поезд массы m = 500 тонн после прекращения тяги тепловоза останавливается под действием силы трения F тр = 0,1 МН (мега-ньютон) через время t = 1 мин. С какой скоростью v шёл поезд до момента прекращения тяги тепловоза? v = …(м/с)
+: 12
I: 214.
S: Какова средняя сила давления F на плечо при стрельбе из автомата, если масса пули m = 10 г, а скорость пули при вылете из ствола v = 300 м/с? Число выстрелов из автомата в единицу времени n = 300 мин– 1. F = … (Н).
+: 15
I: 215.
S: Орудие, имеющее массу ствола М = 500 кг, стреляет в горизонтальном направлении. Масса снаряда m = 5 кг, его начальная скорость v = 460 м/с. При выстреле ствол откатывается на расстояние s = 40 см. Найти среднюю силу торможения F (кН), возникающую в механизме, тормозящем ствол (результат вычисления округлить до целого числа); F = … (килоньютон)
+: 13
I: 216.
S: Человек, стоящий на коньках на гладком льду реки, бросает камень массы m = 0,5 кг. Спустя время t = 2 сек. камень достигает берега, пройдя расстояние s = 20 м. С какой скоростью u начинает скользить конькобежец, если его масса M = 60 кг? Трением пренебречь. (Результат вычисления округлить до второго знака после запятой включительно.)
u = … (м/с)
+: 0,08
I: 217.
S: Тело массы M = 990 г лежит на горизонтальной поверхности. В него попадает пуля массы m = 10 г и застревает в нём. Скорость пули v = 700 м/с и направлена горизонтально. Какой путь s пройдет тело до остановки? Коэффициент трения между телом и поверхностью k = 0,05. (Результат вычисления округлить до целого числа.) (g = 9,8 м/с2) s = … (м)
+: 50
I: 218.
S: Ракета, имеющая вместе с зарядом массу M = 250 г, взлетает вертикально вверх и достигает высоты h = 150 м. Масса заряда m = 50 г. Найти скорость v истечения газов из ракеты (относительно земли), считая, что сгорание заряда происходит мгновенно. (Результат вычисления округлить до целого числа.)
v = … (м/с).
+: 217
I: 219.
S: Масса платформы с орудием и боеприпасами составляет M = 20 тонн. С этой платформы, движущейся со скоростью u = 9 км/час, производится выстрел из орудия. Снаряд массы m = 25 кг вылетает из ствола орудия со скоростью v = 700 м/с (относительно орудия). Найти скорость платформы u 1 (км/час) непосредственно после выстрела, если направления движения платформы и выстрела совпадают. (Результат вычисления округлить до целого числа.)
u 1 = … (км/час).
+: 6
I: 220.
S: Масса платформы с орудием и боеприпасами составляет M = 20 тонн. С этой платформы, движущейся со скоростью u = 9 км/час, производится выстрел из орудия. Снаряд массы m = 25 кг вылетает из ствола орудия со скоростью v = 700 м/с (относительно орудия). Найти скорость платформы u 1 (км/час) непосредственно после выстрела, если направления движения платформы и выстрела противоположны. (Результат вычисления округлить до целого числа.)
u 1 = … (км/час).
+: 12
I: 221.
S: Ядро, летевшее со скоростью v = 200 м/с, разорвалось на два осколка с массами m 1 = 10 кг и m 2 = 5 кг. Скорость первого осколка v 1 = 300 м/с и направлена так же, как и скорость ядра до разрыва. Найти скорость v 2 второго (меньшего) осколка; v 2 = … (м/с).
+: 0
I: 222.
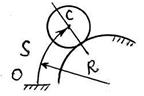 S: Центр масс колеса С движется по окружности радиуса R = 1,6 м согласно закону s = 4ּ t (м). Масса колеса m = 15 кг.
S: Центр масс колеса С движется по окружности радиуса R = 1,6 м согласно закону s = 4ּ t (м). Масса колеса m = 15 кг.
Модуль главного вектора внешних сил, приложенных к колесу равен … (Н)
+: 150
I: 223.
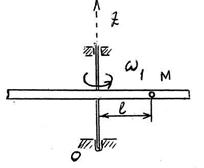 S: Трубка вращается вокруг вертикальной оси Oz, её момент инерции Ј z = 0,075 кгּм2. По трубке под действием внутренних сил системы движется шарик М массой m = 0,1 кг. Когда шарик находится на О z, угловая скорость ω0 = 4 рад/с. Затем угловая скорость становится равной ω1 = 3 рад/с. Это стало на расстоянии l.
S: Трубка вращается вокруг вертикальной оси Oz, её момент инерции Ј z = 0,075 кгּм2. По трубке под действием внутренних сил системы движется шарик М массой m = 0,1 кг. Когда шарик находится на О z, угловая скорость ω0 = 4 рад/с. Затем угловая скорость становится равной ω1 = 3 рад/с. Это стало на расстоянии l.
Определить расстояние l; l = … (м).
+: 0,5
 I: 224.
I: 224.
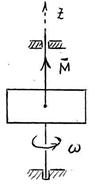
S: Тело вращается вокруг вертикальной оси Oz под действием пары сил с моментом М = 16ּ t (Нּм). При t = 0 тело находилось в покое, а в момент t = 3 с угловая скорость ω = 2 рад/с.
Определить момент инерции (кгּм2) тела относительно оси Oz.
Отметьте правильный ответ.
-: 24; +: 36; -: 42; -: 54
I: 225.
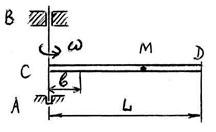 S: Горизонтальная трубка CD может свободно вращаться вокруг вертикальной оси AB. Внутри трубки на расстоянии b = 0,2 м, от оси находится шарик M. В некоторый момент времени трубке сообщается начальная угловая скорость ω 0 = 5 рад/сек. Определить угловую скорость ω трубки в момент, когда шарик вылетит из трубки. Момент инерции трубки относительно оси вращения равен J = 0,7 кгּм2, её длина L = 1 м; шарик считать материальной точкой массы m = 0,5 кг; трением пренебречь. ω = … (рад/с).
S: Горизонтальная трубка CD может свободно вращаться вокруг вертикальной оси AB. Внутри трубки на расстоянии b = 0,2 м, от оси находится шарик M. В некоторый момент времени трубке сообщается начальная угловая скорость ω 0 = 5 рад/сек. Определить угловую скорость ω трубки в момент, когда шарик вылетит из трубки. Момент инерции трубки относительно оси вращения равен J = 0,7 кгּм2, её длина L = 1 м; шарик считать материальной точкой массы m = 0,5 кг; трением пренебречь. ω = … (рад/с).
+: 3
I: 226.
S: Кривошипно-ползунный механизм прикреплён к станине массы M, установленной на гладком горизонтальном фундаменте. Масса ползуна B механизма равна m, причём M = 9ּ m. Пренебрегая массой звеньев OA и AB, длины которых соответственно OA = l, OA и AB = 2ּ l, найти максимальное значение v max скорости станины, если кривошип вращается с постоянной угловой скоростью ω и при t = 0 угол φ = 0 и начальная скорость станины равна нулю.
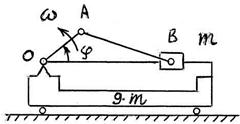
Искомая скорость v max имеет вид v max = Κּωּl. Определить Κ (результат вычисления – с точностью до первого знака после запятой). Κ = ….
+: 0,1
I: 227.
S: Два вагонамасс m 1 = 20 тонн и m 2 = 30 тонн, двигавшиеся навстречу друг другу по горизонтальному прямолинейному участку пути со скоростями v 1 = 3 м/с и v 2 = 2,5 м/с соответственно, сцепляются после соударения. Пренебрегая сопротивлениями движению, определить модуль скорости v сцепа; v = … (м/с).
+: 0,3
I: 228.
S: Через участки трубы постоянного сечения и различной формы со скоростью v протекает жидкость заполняющая всё сечение трубы. Направление установившегося движения жидкости указано на рисунке стрелками. Полагая вес участков трубы и заполняющей их жидкости одинаковыми во всех четырёх случаях, установить, в каком из этих случаев сила нормального давления трубы на основание оказывается наибольшей
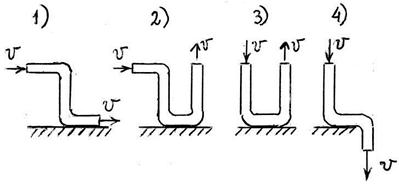
-: 1); -: 2); +: 3); -: 4)
I: 229.
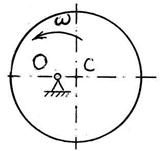 S: Диск массой m = 20 кг вращается равномерно вокруг неподвижной оси с угловой скоростью ω = 10 рад/с. Центр тяжести удалён от оси вращения на расстояние ОС = 0,5 см.
S: Диск массой m = 20 кг вращается равномерно вокруг неподвижной оси с угловой скоростью ω = 10 рад/с. Центр тяжести удалён от оси вращения на расстояние ОС = 0,5 см.
Модуль главного вектора внешних сил, приложенных к диску, равен … (Н).
+: 10
I: 230.
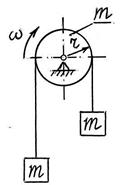 S: Два груза одинаковой массы m = 2 кг каждый закреплены по концам невесомого нерастяжимого каната, переброшенного через однородный шкив массы m = 2 кг и радиуса r = 0,1 м. Зная угловую скорость вращения ω = 5 рад/с шкива и пренебрегая проскальзыванием каната относительно шкива, определить модуль количества движения | Q | данной механической системы; | Q | = … (кгּм/с).
S: Два груза одинаковой массы m = 2 кг каждый закреплены по концам невесомого нерастяжимого каната, переброшенного через однородный шкив массы m = 2 кг и радиуса r = 0,1 м. Зная угловую скорость вращения ω = 5 рад/с шкива и пренебрегая проскальзыванием каната относительно шкива, определить модуль количества движения | Q | данной механической системы; | Q | = … (кгּм/с).
+: 0
I: 231.
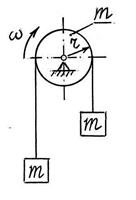 S: Два груза одинаковой массы m = 2 кг каждый закреплены по концам невесомого нерастяжимого каната, переброшенного через однородный шкив массы m = 2 кг и радиуса r = 0,1 м. Зная угловую скорость вращения ω = 5 рад/с шкива и пренебрегая проскальзыванием каната относительно шкива, определить модуль кинетического момента | K z| данной механической системы относительно оси вращения (числовой результат определить с точностью до второго знака после запятой);
S: Два груза одинаковой массы m = 2 кг каждый закреплены по концам невесомого нерастяжимого каната, переброшенного через однородный шкив массы m = 2 кг и радиуса r = 0,1 м. Зная угловую скорость вращения ω = 5 рад/с шкива и пренебрегая проскальзыванием каната относительно шкива, определить модуль кинетического момента | K z| данной механической системы относительно оси вращения (числовой результат определить с точностью до второго знака после запятой);
| K z| = … (кгּм2/с).
+: 0,25
I: 232.
S: Снаряд массы m = 12 кг, летевший со скоростью v = 800 м/с, разорвался в воздухе на 240 равных по массе осколков. Разлёт осколков в системе отсчёта, связанной с первоначальным снарядом, является сферически симметричным, и скорость каждого осколка в этой системе отсчёта равна v отн = 600 м/с. Модуль количества движения системы осколков относительно земли равен … (кгּм/с).
+: 9600
I: 233.
S: Шарик массой m = 100 г свободно упал на горизонтальную площадку, имея в момент удара скорость v = 10 м/с. Найти модуль изменения количества движения при абсолютно неупругом | Q неупруг| и абсолютно упругом | Q упруг| ударах;
| Q неупруг| = … (кгּм/с), | Q упруг| = … (кгּм/с).
+: 1*2
I: 234.
S: Материальная точка массой 1 кг равномерно движется по окружности со скоростью 10 м/с. Найти модуль изменения количества движения за одну четверть периода |Δ Q 1/4|; половину периода |Δ Q 1/2|; целый период |Δ Q 1| (результат вычисления округлить до целого числа);
|Δ Q 1/4| = … (кгּм/с), |Δ Q 1/2| = … (кгּм/с), |Δ Q 1| = … (кгּм/с).
+: 14*20*0
I: 235.
S: Охотник стреляет из ружья с лодки по направлению её движения. Какую скорость v имела лодка, если она остановилась после быстро следующих друг за другом выстрелов? Масса охотника с лодкой 200 кг, масса заряда 20 г. Скорость вылета дроби и пороховых газов 500 м/с. (Числовой результат определить с точностью до первого знака после запятой.) v = … (м/с).
+: 0,1
I: 236.
S: Вагон массой 20 т, движущийся со скоростью 0,3 м/с, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после взаимодействия, если удар неупругий? (Числовой результат определить с точностью до второго знака после запятой.)
v = … (м/с).
+: 0,24
I: 237.
S: С лодки массой 200 кг, движущейся со скоростью v =1 м/с, прыгает мальчик массой 50 кг в горизонтальном направлении с кормы в сторону, противоположную движению лодки, со скоростью 6 м/с относительно лодки. Какова скорость v 1 лодки после прыжка мальчика? (Числовой результат определить с точностью до первого знака после запятой.) v 1 = … (м/с).
+: 2,5
I: 238.
S: С лодки массой 200 кг, движущейся со скоростью v =1 м/с, прыгает мальчик массой 50 кг в горизонтальном направлении с носа лодки по ходу движения лодки со скоростью 6 м/с относительно лодки. Какова скорость v 1 лодки после прыжка мальчика? (Числовой результат определить с точностью до первого знака после запятой. Будьте внимательны со знаком значения v 1!) v 1 = … (м/с).
+: - 0,5
I: 239.
S: Мяч массой 100 г, летевший со скоростью 20 м/с, ударился о горизонтальную плоскость. Угол падения (угол между направлением скорости и перпендикуляром к плоскости) равен 60о. Удар абсолютно упругий, а угол отражения равен углу падения. Модуль изменения количества движения равен … (кгּм/с).
+: 2
I: 240.
S: Какую скорость относительно ракетницы приобретает ракета массой 615 г, если газы массой 15 г вылетают из неё со скоростью 800 м/с?
Скорость ракеты равна … (м/с).
+: 20
Date: 2015-05-18; view: 2097; Нарушение авторских прав