Тема 4. Потенциальное силовое поле. Работа потенциальной силы

I: 121.

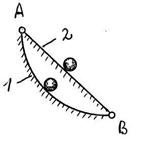S: Тяжёлая материальная точка может перемещаться в вертикальной плоскости из положения А в положение В по дуге окружности 1 или отрезку наклонной прямой 2. Будет ли одинакова работа силы тяжести при этих перемещениях?

Отметьте правильный ответ.

+: Одинакова

-: Неодинакова

I: 122.

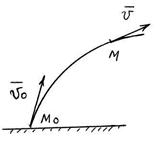S: Материальная точка массой m = 0,5 кг брошена с поверхности Земли с начальной скоростью v ₀ = 20 м/с и в положении М имеет скорость v = 12 м/с. Определить работу силы тяжести (Дж) при перемещении точки из положения М ₀ в положение М.

Отметьте правильный ответ.

+: – 64; -: 0; -: 64; -: 128; -: – 128

I: 123.

S: Груз М весом Р = 20 Н, прикреплённый к невесомой нити длиной l = ОМ = 40 см, начинает двигаться из состояния покоя. Определить: 1) работу силы тяжести А (Р) на перемещении М₁М₂; 2) скорость v груза М, когда он займёт положение М₂. Принять g = 10 м/с².

1) = … (Дж), 2) 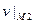= … (м/с).

+: 4*2

I: 124.

S: Тело А находится на гладкой горизонтальной плоскости. К телу прикреплена пружина жёсткости с = 100 Н/см, второй конец которой прикреплён к шарниру О₁. Длина недеформированной пружины равна l ₀ = 20 см (см. рис.). В положении равновесия тела длина пружины равна l = О₁О = 24 см. Определить модуль работы |A_OM| упругой силы пружины на перемещении груза тела на расстояние x = 10 см;

|A_OM| = … (Дж),

+: 10

I: 125.

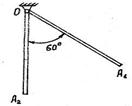S: Стержень длиной l = 2 м и весом Р = 30 Н начинает двигаться из состояния покоя ОА₁ без начальной скорости. Определить: 1) работу силы тяжести А (Р) при его перемещении из положения ОА₁в положение ОА₂; 2) угловую скорость ω стержня в момент, когда он займёт положение ОА₂. Результат вычисления округлить до ближайшего целого числа. Принять g = 10 м/с².

1) 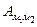= … (Дж), 2) ω | 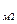= … (рад/с).

+: 15*3

I: 126.

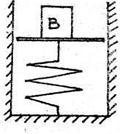S: Груз В весом Р = 200 Н без начальной скорости помещают на неподвижную плиту, прикреплённую к вертикальной пружине, и плавно опускают. Определить коэффициент жёсткости пружины с, если наибольшее сжатие пружины под весом плиты λ _max = 10 см.

c = … (Н/см).

+: 20

I: 127.

S: Однородный диск массы m скатывается вниз по наклонной плоскости без скольжения без начальной скорости из положения, когда пружина не деформирована. Коэффициент жёсткости пружины равен с.

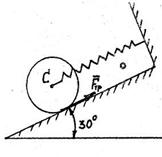Определить: 1) кинетическую энергию диска Т в произвольный момент времени, выразив её через скорость центра масс диска v _с; 2) работу силы трения А (F _тр) на перемещении, когда центр диска пройдёт путь s _с = s; 3) работу силы тяжести А (Р) диска на этом же перемещении. 1) Т = …ּ mּv _с²; 2) А (F _тр) = …ּ mּgּcos 30^oּ s _cּ/ R; 3) А (Р) = … ּ mּgּs _c (вместо многоточия подставить соответствующие множители в виде десятичной дроби).

+: 0,75*0*0,5

I: 128.

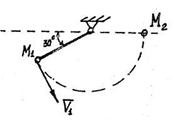S: Груз М весом Р подвешен на невесомой нерастяжимой нити длиной l. В начальный момент времени груз находился в положении М₁.

Определить: 1) работу силы тяжести А (Р) на перемещении груза М₁М₂; 2) какую минимальную скорость v ₁ необходимо сообщить грузу, чтобы он достиг положения М₂. (Начальный угол наклона стержня 30^о)

1) А (Р) = … ּ Рּl; 2) v ₁ = …ּ 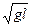(вместо многоточия подставить соответствующие множители в виде десятичной дроби).

+: – 0,5*1

I: 129.

S: Точечный груз М массы m ₁ прикреплён к стержню ОМ длиной l и массы m ₂ = 0,6ּ m ₁.Стержень ОМ вращается вокруг точки О.

Определить: 1) кинетическую энергию Т системы в момент времени, когда угловая скорость стержня равна ω; 2) работу силы тяжести А стержня при его перемещении из положения ОВ в положение ОD (угол BOD равен 30^о).

1) Т = …ּ m ₁ּ l ²ּ ω ² ; 2) А = …ּ m ₁ּ gּl

(вместо многоточия подставить соответствующие множители в виде десятичной дроби, включая второй знак после запятой).

+: 0,60*0,65

I: 130.

S: Груз М весом Р = 200 Н прикрепили к середине неизогнутой балки жёсткости с = 100 Н/см и отпустили резко без начальной скорости. Определить наибольший прогиб λ_max середины балки; λ_max = … (см).

+: 4

I: 131.

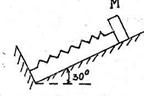S: Груз М весом Р = 300 Н прикрепили к концу недеформированной пружины жёсткости с = 20 Н/см и опустили резко без начальной скорости. Определить: 1) работу силы тяжести А (Р) на перемещении груза S = 10 см вниз по наклонной плоскости (под углом 30^о к горизонтали): 2) работу упругой силы пружины А (F _упр) на этом же перемещении груза;

3) максимальное сжатие пружины | λ_max |.

1) А (Р) = … (Дж); 2) А (F _упр) = … (Дж); 3) | λ_max | = … (см).

+: 15*– 10*15

I: 132.

S: К невесомому стержню ОА длиной l = 2 ּr прикрепили однородный диск веса Q и радиуса r. Вычислить: 1) кинетическую энергию диска Т в момент времени, когда угловая скорость стержня равна ω; 2) работу силы тяжести А (Q) диска при перемещении стержня из положения ОА в положение ОА₁.

1) Т = … ּ mּr ²ּ ω ² ; 2) А = … ּ Qּr (вместо многоточия подставить соответствующие множители в виде десятичной дроби).

+: 4,75*3

I: 133.

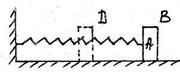S: К пружине жёсткости с = 40 Н/см прикреплён груз А. Определить работу упругой силы пружины А (F _упр) при перемещении груза А из положения В в положение D, если в положении В пружина была растянута на λ _В = 3 см, а в положении сжата на |λ_D| = 2 см; А _BD = …(Дж).

+: 1

I: 134.

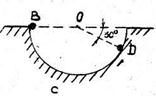
S: Шарик, размерами которого пренебрегаем, скатывается из точки В по круглому гладкому жёлобу радиуса r без начальной скорости. Определить скорость шарика v _D в точке D;

v _D = …ּ 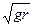(вместо многоточия подставить соответствующий множитель в виде десятичной дроби).

+: 1

I: 135.

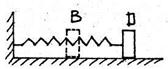S: Определить работу А упругой силы пружины жёсткости с = 40 Н/см при перемещении груза из положения В в положение D, если в положении В пружина была сжата на |λ_В| = 1см, а в положении D растянута на λ_D = 2 см.

А _BD = …(Дж).

+: – 0,6

I: 136.

S: Матер. точка находится в силовом поле

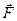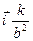= ּ (x ² ּy ² + b ² ּy ² ) + (x ³ ּy + b ² ּxּy) (H)

(k и b – постоянные). Является ли силовое поле 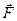потенциальным?

Отметьте правильный ответ.

-: Да; +: Нет

I: 137.

S: Матер. точка находится в силовом пол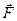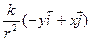е = , где

r ² = x ² + y ² + z ², k – заданная постоянная). Является ли силовое поле 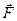потенциальным?

Отметьте правильный ответ.

-: Да; +: Нет

I: 138.

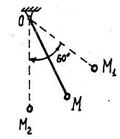
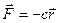S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру , где 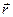- радиус-вектор точки, c = 20 Н/см. Вычислить работу А ₁₂ силы 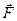при перемещении матер. точки из точки М ₁ в точку М ₂ (см. рис.);

а = 6 см, b = 8 см. А ₁₂ = … (Дж).

+: 0

I: 139.

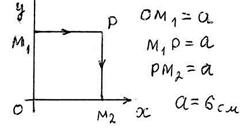S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру 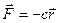, где 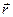- радиус-вектор точки, c = 20 Н/см. Вычислить работу А ₁₂ силы 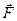при перемещении матер. точки по пути М ₁ РМ ₂ (см. рис.); ОМ ₁ = М ₁ Р = РМ ₂ = а = 6 см. А ₁₂ = … (Дж).

+: 0

I: 140.

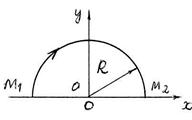S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру 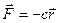, где 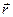- радиус-вектор точки, c = 20 Н/см. Вычислить работу А ₁₂ силы 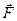при перемещении матер. точки из точки М ₁ в точку М ₂ по дуге полуокружности радиуса R = 10 см (см. рис.).

А ₁₂ = … (Дж).

+: 0

I: 141.

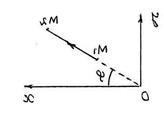S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы отталкивания 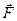= 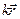/ r ³ от силового центра О, убывающей по величине обратно пропорционально квадрату расстояния от точки до силового центра О, F = k / r ², k = 100 (Н/м²). Вычислить работу А ₁₂ силы 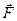при перемещении матер. точки радиально из точки М ₁ в точку М ₂ (см. рис.); ОМ ₁ = 10 м, ОМ ₂ = 20 м (см. рис.). А ₁₂ = … (Дж).

+: 5

I: 142.

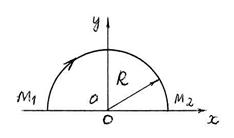S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы отталкивания 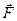= 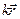/ r ³ от силового центра О, убывающей по величине обратно пропорционально квадрату расстояния от точки до силового центра О, F = k / r ², k = 100 (Н/м²). Вычислить работу А ₁₂ силы 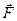при перемещении матер. точки радиально из точки М ₁ в точку М ₂ по дуге полуокружности радиуса R = 10 м (см. рис.).

А ₁₂ = … (Дж).

+: 0.

I: 143.

S: Матер. точка массы m движется по окружности радиуса r в поле центральной силы, имея потенциальную энергию П(r) = – 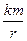, где k = const. (Центр окружности совпадает с силовым центром.) Определить значение скорости v точки при следующих числовых данных параметров: k = 9 м³/сек² и r = 4 м.

v = … (м/с).

+: 1,5

I: 144.

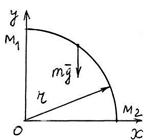S: Матер. точка массы m = 2 кг перемещается в вертикальной плоскости Oxy. Определить работу А ₁₂ силы тяжести 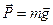при перемещении матер. точки по дуге М₁М₂ четверти окружности радиуса R = 10 м (см. рис.). Ускорение свободного падения приять равным g = 9,8 м/с².

А ₁₂ = … (Дж).

+: 196

I: 145.

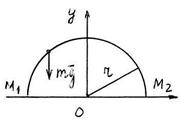S: Матер. точка массы m = 2 кг перемещается в вертикальной плоскости Oxy. Определить работу А₁₂ силы тяжести 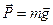при перемещении матер. точки по дуге М₁М₂ полуокружности радиуса R = 10 м (см. рис.). Ускорение свободного падения приять равным g = 9,8 м/с².

А ₁₂ = … (Дж).

+: 0.

I: 146.

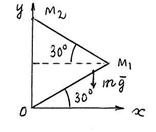S: Матер. точка массы m = 2 кг перемещается в вертикальной плоскости Oxy. Определить работу А₁₂ силы тяжести 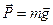при перемещении матер. точки по двум отрезкам ОМ₁ и М₁М₂; высота ОМ₂ = h =10 м (см. рис.). Ускорение свободного падения приять равным g = 9,8 м/с².

А ₁₂ = … (Дж).

+: – 196

I: 147.

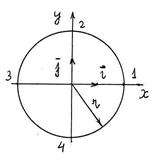S: Вычислить работу силы непотенциального силового поля

=

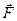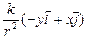
(r ² = x ² + y ², k – заданная постоянная) по контуру 1-2-3-4-1 радиуса r (см. рис.).

Выражение искомой работы А _1-2-3-4-1 приводится к виду: А = Qּπּk. Определить значение Q; Q = …

+: 2.

I: 148.

S: К пружине жёсткости с = 10 Н/см, один конец которой закреплён, подвешен груз веса Р = 49 (Н), лежащий на подставке так, что пружина не растянута (см. рис.). Без толчка подставка убирается. Найти максимальное натяжение Т _max пружины;

Т _max = … (Н).

+: 98

I: 149.

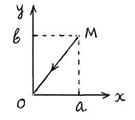S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру 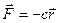, где 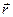- радиус-вектор точки, c = 20 Н/см. Вычислить работу А ₁₂ силы 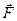при перемещении матер. точки из точки М в точку О (см. рис.); а = 6 см, b = 8 см.

А _МО = … (Дж).

+: 10

I: 150.

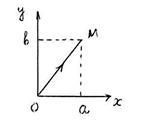S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру 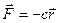, где 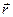- радиус-вектор точки, c = 20 Н/см. Вычислить работу А ₁₂ силы 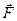при перемещении матер. точки из точки О в точку М (см. рис.); а = 6 см, b = 8 см.

А _ОМ = … (Дж).

+: – 10

I: 151.

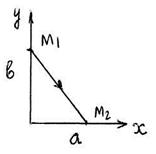S: Матер. точка массы m движется в горизонтальной плоскости Oxy под действием силы, пропорциональной смещению точки от точки от центра О и направленной к этому центру 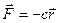, где 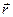- радиус-вектор точки, c = 20 Н/см. Вычислить работу А ₁₂ силы 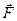при перемещении матер. точки из точки М ₁ в точку М ₂ (см. рис.); ОМ₁ = b = 8 см, OM₂ = a = 6 см. А ₁₂ = … (Дж). +: 2,8

I: 152.

S: Ускорение свободного падения у поверхности Луны g = 1,623 м/с². Радиус Луны R = 1728 км. Вычислить первую космическую скорость v _{косм 1} для Луны. (Результат вычисления округлить до целого числа.) v _{косм 1} = … (м/с).

+: 1675

I: 153.

S: Ускорение свободного падения у поверхности планеты Марс g = 3,71 м/с². Радиус Марса R = 3393 км. Вычислить первую космическую скорость v _косм1 для Марса. (Результат вычисления округлить до целого числа с выбором чётной цифры округления.) v _{косм 1} = … (м/с).

+: 3548

I: 154.

S: Ускорение свободного падения у поверхности Земли g = 9,81 м/с². Радиус Земли R = 6378 км. Вычислить первую космическую скорость v _{косм 1} для Земли. (Результат вычисления округлить до целого числа с выбором чётной цифры округления.) v _{косм 1} = … (м/с).

+: 7910

I: 155.

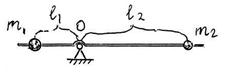S: На рис. изображена штанга, которая может вращаться вокруг горизонтальной оси шарнира О. Плечи штанги l ₁ = 30 см и l ₂ = 70 см. На концах штанги закреплены точечные грузы с массами m ₁ = 7 кг и m ₂ = 3 кг. Штанга совершает поворот вокруг оси О в вертикальной плоскости на угол 90^о по часовой стрелке.

Вычислить работу силы тяжести при этом повороте. Массой штанги пренебречь. Ускорение свободного падения принять равным g = 9,8 м/с².

А = … (Дж).

+: 0.

I: 156.

S: На рис. изображена штанга, которая может вращаться вокруг горизонтальной оси шарнира О. Плечи штанги l ₁ = 30 см и l ₂ = 70 см. На концах штанги закреплены точечные грузы с массами m ₁ = 6 кг и m ₂ = 4 кг. Штанга совершает поворот вокруг оси О в вертикальной плоскости на угол 90^о по часовой стрелке.

Вычислить работу силы тяжести при этом повороте. Массой штанги пренебречь. Ускорение свободного падения принять равным g = 9,8 м/с². А = … (Дж).

+: 9,8

I: 157.

S: На рис. изображена штанга, которая может вращаться вокруг горизонтальной оси шарнира О. Плечи штанги l ₁ = 30 см и l ₂ = 70 см. На концах штанги закреплены точечные грузы с массами m ₁ = 6 кг и m ₂ = 4 кг. Штанга совершает поворот вокруг оси О в вертикальной плоскости на угол 90^о против часовой стрелке.

Вычислить работу силы тяжести при этом повороте. Массой штанги пренебречь. Ускорение свободного падения принять равным g = 9,8 м/с². А = … (Дж).

+: – 9,8

I: 158.

S: Груз массой m прикреплён к правому концу пружины, левый конец которой закреплён в стене. В начальном положении пружина не была деформирована. Ось x направлена вдоль оси пружины, причём начало отсчёта находится в правом конце не деформированной пружины.

Проекция силы упругости пружины равна F_x = – cּx – b ּ x ³, где x – удлинение пружины; параметры c и b имеют следующие значения: c = 2000 Н/м, b = 4 Н/м³. Вычислить работу упругой силы пружины при перемещении груза на расстояние s = 1 м. А = … (Дж)

+: – 1001

I: 159.

S: К матер. точке В присоединены две одинаковые пружины жёсткости c = 40 Н/см. Другой конец первой пружины закреплён в точке О₁, а второй конец второй пружины в – точке О₂ (см. рис.). Длина недеформированной пружины равна l ₀ = 5 см. О₁О = ОО₂ = l ₀. Вычислить работу сил упругости при перемещении матер. точки в точку М с координатами x _М = 0, y _М = 2ּ l ₀ . (Результат вычисления округлить до ближайшего целого числа.) А _ОМ = … (Дж).

+: – 15

I: 160.

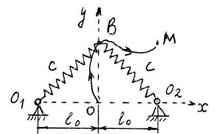S: К матер. точке В присоединены две одинаковые пружины жёсткости c = 40 Н/см. Другой конец первой пружины закреплён в точке О₁, а второй конец второй пружины в – точке О₂ (см. рис.). Длина недеформированной пружины равна l ₀ = 5 см. О₁О = ОО₂ = l ₀. Вычислить работу сил упругости при перемещении матер. точки в точку М с координатами x _М = l ₀, y _М = l ₀ . (Результат вычисления округлить до первого знака после запятой включительно.) А _ОМ = … (Дж).

+: – 7,6

Date: 2015-05-18; view: 994; Нарушение авторских прав