Эффект Зеемана. Зная полный магнитный момент атома, можно определить влияние внешнего магнитного поля на его спектр

Зная полный магнитный момент атома, можно определить влияние внешнего магнитного поля на его спектр. Происходящее под действием внешнего магнитного поля расщепление энергетических уровней атомов названо эффектом Зеемана в честь открывшего его нидерландского ученого Питера Зеемана. В результате в спектрах излучающих атомов наблюдается расщепление отдельных линий на несколько компонент. Степень расщепления, т.е. отличие энергий двух соседних уровней, зависит от величины магнитного поля, т.е. чем сильнее магнитное поле, тем больше разница энергий между расщепившимися линиями. Зеемановское расщепление обусловлено тем, что атом, обладающий магнитным моментом, приобретает в магнитном поле дополнительную энергию:

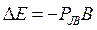(8.8)

где проекция магнитного момента атома P_JB задается на направление магнитного поля и равна, согласно формуле (7.6), .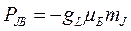

Подставив это выражение в формулу (8.8), получим величину расщепления энергетических уровней атома в магнитном поле B:

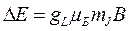(8.9)

где m_J = 0, ±1, ±2,..., ± J.

Учитывая, что m_J может принимать 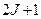различных значений, получаем, что каждая линия должна расщепиться на 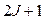отдельных линий. Величина расщепления линий будет зависеть от множителя Ланде, считаемого по формуле (8.7).

Рассмотрим случай, когда линии излучения атома не имеют тонкой структуры, обусловленной спин-орбитальным взаимодействием электрона (см. выше). В отсутствие поля в спектре такого атома наблюдаются одиночные линии. Ограничимся рассмотрением одной из них, пусть ее энергия, соответствующая этой линии, равна При наложении внешнего магнитного поля происходит расщепление на 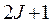уровней, в спектре излучения разумно ожидать при этом появление соответствующего числа компонент вместо указанной линии.

Однако, как уже говорилось, если спин-орбитальное взаимодействие слабо, то полный момент атома складывается из полного орбитального и полного спинового моментов, не сложно показать, что в таком случае множитель Ланде равен единице.

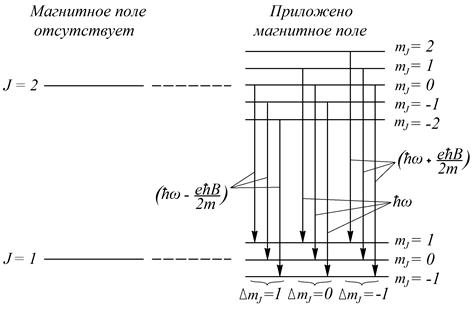
Рис. 8.1. Нормальный эффект Зеемана

Следовательно, уровни с различным значением m_J разделены друг от друга энергетическими промежутками, равными:

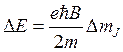(8.10)

А поскольку переходы в атомах подчиняются правилам отбора:

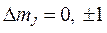(8.11)

то в спектре излучения атома появляются только линии, для которых:

(8.12)

Смещение частоты линий в спектре излучения, следовательно, может быть равно: 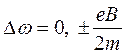(8.13)

Таким образом, в спектре атома, подверженного действию магнитного поля, вместо отдельных линий наблюдаются триплетные группы линий (рис. 8.1). Эффект расщепления одиночных линий в квантовой механике называют снятием вырождения энергетических уровней (о кратности вырождения см. раздел 7). Следует заметить, что расщепление испытывают только те энергетические состояния, значение J которых отлично от нуля.

Описанное явление наблюдается в основном для легких атомов и называется простым (или нормальным) эффектом Зеемана.

Существует также сложный (или аномальный) эффект Зеемана. Он наблюдается для тяжелых атомов. Сложный эффект Зеемана объясняется существованием спин-орбитального взаимодействия. Для тяжелых атомов оно особенно заметно. Его учет при вычислении 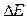приводит к дополнительному снятию вырождения, т.е. к появлению в спектре дополнительных компонент (усложнение спектра).

Date: 2015-05-18; view: 731; Нарушение авторских прав