
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Принцип Паули. В случае более сложных, чем водород, атомов, имеющих несколько электронов, можно считать, что каждый электрон движется в усредненном поле ядра и остальных
|
|
В случае более сложных, чем водород, атомов, имеющих несколько электронов, можно считать, что каждый электрон движется в усредненном поле ядра и остальных электронов. Это поле уже не является пропорциональным 1/r2 (как кулоновское), но оно обладает центральной симметрией. То есть, введя определенные поправки, можно решить задачу на собственные функции и собственные значения для любого для атома аналогично задаче об атоме водорода.
Состояние электрона в этом случае определяется четырьмя квантовыми числами:
главным n (n = 1, 2, 3,...)
орбитальным l (l = 0, 1, 2,..., n – 1)
магнитным ml (ml = – l,..., –1, 0, 1,..., + l)
спиновым ms (ms = –1/2, +1/2).
Энергия каждого состояния в основном определяется параметрами n и l, и лишь незначительно ml и ms. Чем больше n и l, тем больше энергия. В невозбужденном состоянии атома электроны в нем должны располагаться на самых низких из доступных им энергетических уровнях, а таковым является 1s состояние. То есть, ожидается, что все электроны в атомах должны располагаться именно на нем. Однако опыт показывает, что это не так. Реальная ситуация отражена в одном из основных законов квантовой механики, называемом принципом Паули (принципом запрета или исключения). Он справедлив для частиц, обладающих полуцелым спином, и для атомов гласит следующее: в одном и том же атоме не может быть двух электронов, обладающих одинаковой совокупностью четырех квантовых чисел n, l, ml, ms. Или в общем случае: в любой квантовой системе не возможно обнаружить две частицы, обладающих полуцелым спином и находящихся в одном и том же состоянии.
Совокупность электронов с данным n образует оболочку. Оболочки принято обозначать прописными латинскими буквами K, L, M, N, O, P и т.д.
Каждая оболочка в свою очередь подразделяется на подоболочки, отличающиеся значением параметра l (s, p, d, f,...). Можно показать, что при данном n существует 2n2 состояний, отличающихся друг от друга остальными тремя квантовыми числами (орбитальным l, магнитным ml и спиновым ms). Следовательно в атоме в состояниях с данным значением n могут находиться не более 2n2 электронов, то есть в состоянии с:
n = 1 могут находиться 2 электрона, они составляют K -оболочку,
n = 2 могут находиться 8 электронов, составляющих L -оболочку,
n = 3 могут находиться 18 электронов, составляющих M -оболочку,
n = 4 могут находиться 32 электрона, составляющих N -оболочку, и т.д.
Заполнение оболочек в атомах в соответствии с принципом Паули начинается с первой (K -оболочки): атомы с единственной непустой оболочкой – это водород и гелий (см. табл.). По мере увеличения числа электронов в атоме заполненными оказываются и следующие оболочки. Повторение химических свойств элемента совпадает со степенью заполнения внешней оболочки. Так атомы, у которых внешняя оболочка содержит один электрон, обладают свойствами щелочных металлов (кроме водорода). Напротив, атомы с полностью заполненной внешней оболочкой являются инертными газами. Вплоть до калия (№19) заполнение оболочек происходит по порядку.
Для калия же наблюдается аномальное заполнение – прежде чем заполнится полностью M -оболочка, начинается заполнение следующей N -оболочки. Это связано с тем, что энергия подоболочки 3d оказывается выше подоболочки 4s. Природный принцип стремления любой системы к минимуму энергии приводит к тому, что электроны сначала заполняют боле низкое энергетическое состояние, т.е. 4s. После заполнения подоболочки 4s будет заполняться 3d, и только после нее подоболочка 4p, так как ее энергия будет еще больше.
Таким образом, каждый атом состоит из определенного числа электронов. Энергетические состояния атома могут быть рассчитаны с помощью уравнений, аналогичных уравнению Шредингера.
Заполнение оболочек атомов электронами
| Элемент (№ и название) | K | L | M | N | |||||
| 1s | 2s | 2p | 3s | 3p | 3d | 4s | 4p | 4d | |
| 1 H | - | - | - | - | - | - | - | - | |
| 2 He | - | - | - | - | - | - | - | - | |
| 3 Li | - | - | - | - | - | - | - | ||
| 4 Be | - | - | - | - | - | - | - | ||
| 5 B | - | - | - | - | - | - | |||
| 6 C | - | - | - | - | - | - | |||
| 7 N | - | - | - | - | - | - | |||
| 8 O | - | - | - | - | - | - | |||
| 9 F | - | - | - | - | - | - | |||
| 10 Ne | - | - | - | - | - | - | |||
| 11 Na | - | - | - | - | - | ||||
| 12 Mg | - | - | - | - | - | ||||
| 13 Al | - | - | - | - | |||||
| 14 Si | - | - | - | - | |||||
| 15 P | - | - | - | - | |||||
| 16 S | - | - | - | - | |||||
| 17 Cl | - | - | - | - | |||||
| 18 Ar | - | - | - | - | |||||
| 19 K | - | - | - | ||||||
| 20 Ca | - | - | - | ||||||
| 21 Sc | - | - | |||||||
| 22 Ti | - | - | |||||||
| 23 V | - | - | |||||||
| 24 Cr | - | - | |||||||
| 25 Mn | - | - | |||||||
| 26 Fe | - | - | |||||||
| 27 Co | - | - | |||||||
| 28 Ni | - | - | |||||||
| 29 Cu | - | - | |||||||
| 30 Zn | - | - | |||||||
| 31 Ga | - | ||||||||
| 32 Ge | - | ||||||||
| 33 As | - | ||||||||
| 34 Se | - | ||||||||
| 35 Br | - | ||||||||
| 36 Kr | - |
Результирующий момент многоэлектронного атома будет складываться из орбитальных M и собственных MS моментов всех электронов. Существуют специальные правила, по которым рассчитывают результирующий момент атома. Назовем атомным остатком атом, лишенный внешних валентных электронов. Можно показать, что момент атомного остатка равен нулю. Тогда полный момент атома будет складываться из моментов валентных электронов.
Существует два типа атомов, для которых полный момент находится по одному из приведенных ниже правил:
1) в атомах более распространенного типа взаимодействие между орбитальными моментами Ml электронов в атоме сильнее, чем взаимодействие между орбитальным Ml и спиновым Ms моментами каждого электрона, в этом случае сначала находят отдельно результирующие орбитальный и спиновый моменты всех электронов в атоме, затем полученные моменты складываются в полный момент атома.
2) в тяжелых атомах усиливается взаимодействие между орбитальным и спиновым моментами для каждого электрона в атоме, в этом случае сначала находят полный момент отдельного электрона, полный момент атома складывается из полных моментов электронов, входящих в состав атома
Величина полного механического момента атома MJ равна:
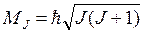 (8.1)
(8.1)
определяется квантовым числом J, которое может быть равно:
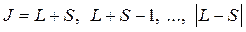 (8.2)
(8.2)
где S, а следовательно и спин атома, может быть как целым, так и полуцелым, в зависимости от того, четное или нечетное число валентных электронов в атоме:
– при четном числе электронов S принимает значение от 0 (если спины попарно компенсируют друг друга) до N/2 (если все спины параллельны друг другу),
– при нечетном числе электронов минимальное S может быть равно 1/2 (когда все кроме одного спины компенсируют друг друга), максимальное S = N/2 (когда все спины параллельны);
число L складывается из квантовых чисел l и может принимать целое значение от 0 (когда l всех электронов равно нулю) до N∙ (n – 1), где n – главное квантовое число валентного уровня, N – число валентных электронов.
Состояние атома полностью описывается тремя квантовыми числами L, S, J. Для обозначения определенных состояний атома используют схематическую запись: 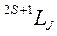 , куда входят указанные квантовые числа.
, куда входят указанные квантовые числа.
Вместо численных значений квантового числа L принято использовать прописные буквенные обозначения: S, P, D, E, F и далее по алфавиту (см. обозначения для атома водорода). В случае, когда S < L, (2 S +1) задает мультиплетность энергетического уровня. Если S > L, мультиплетность равна (2 L +1), однако в верхнем индексе все равно указывается S, чтобы не утерять информацию о спиновом состоянии атома.
Так же, как для атома водорода, момент импульса многоэлектронного атома может иметь строго определенные направления в пространстве, поэтому проекция момента импульса на заданное направление квантуется по правилу: 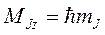 (8.3)
(8.3)
где квантовое число mJ может принимать значения mJ = 0, ±1, ±2,..., ± J, и при переходах атома между состояниями подчиняется правилу отбора:
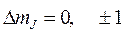 (8.4)
(8.4)
Полному механическому моменту атома соответствует полный магнитный момент: 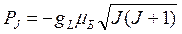 (8.5)
(8.5)
Его направление которого определяется по величине проекции на выделенное направление: 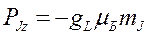 (8.6)
(8.6)
где gL, называемый множителем Ланде, вычисляется по формуле:
 (8.7)
(8.7)
Date: 2015-05-18; view: 631; Нарушение авторских прав